吴恩达机器学习打卡day4

本系列文档按课程视频的章节（P+第几集）进行分类，记录了学习时的一些知识点，方便自己复习。

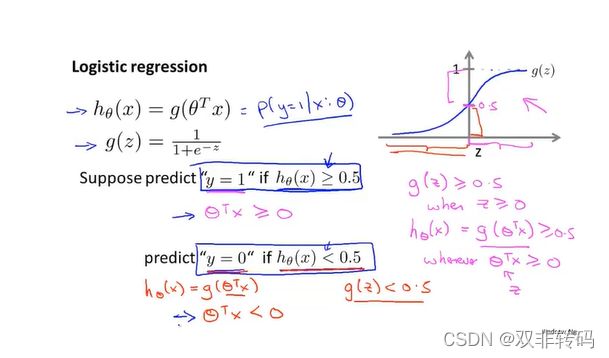
课程视频P32——分类

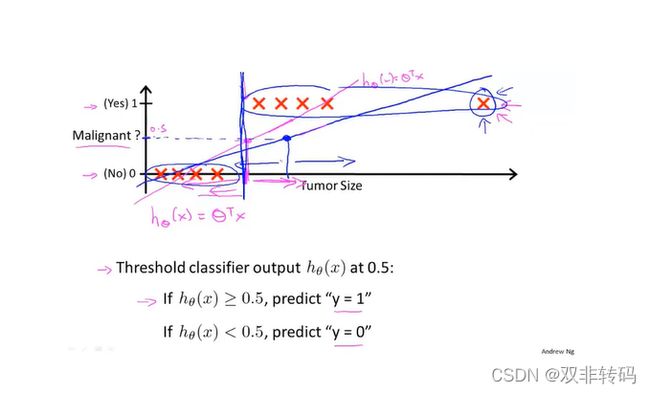
图1 表示最基础的分类原理，当类别只有0，1两种情况时，以0.5为阈值（threshold，当$h_{\theta }(x)$超过0.5时，就判定为1，否则为0。

图1  

但是这种方式过于“一刀切”，如图2 ，当出现一个很横坐标$h_{\theta }(x)$很大的数据时，预测曲线就不得不为了“迁就”它而发生很大改变，导致容易出现很大的误差。

图2  

因此，最好的方法是在做这种0，1分类时，最好将$h_{\theta }(x)$的值预先特征缩放到(0,1)的范围内。

图3  

课程视频P33

图4 表示了除了线性曲线外的另一种代价函数$h_{\theta }(x)$形式，称为log函数(Logistic funtion), 其可将$h_{\theta }(x)$的值域限制在(0,1)范围内。

图4  

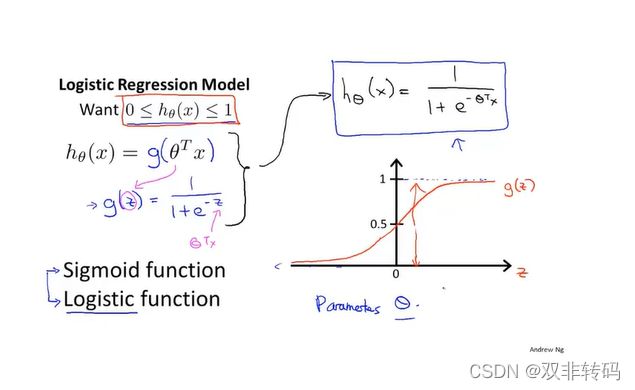
*除了$h_{\theta }(x)$的函数表达式变化之后，其他都不变，同样可以用矩阵和向量的形式来表示其关系。

图5  

课程视频P34——决策界限(Decision boundary)

** 同样表示最基础的分类原理，当类别只有0，1两种情况时，以0.5为阈值（threshold，当$h_{\theta }(x)$超过0.5时，就判定为1，否则为0。**

图6  

** 图7 表示了决策界限(Decision boundary), 以一条线即可完美分类，线的上侧是一类，下侧是另一类。**

图7  

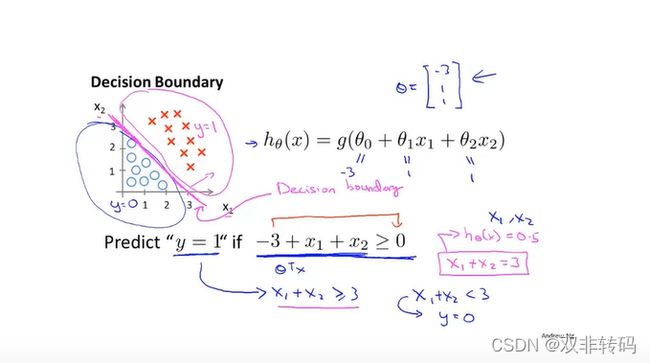
图8 展示了另一种情况下的决策界限(Decision boundary), 以一条线即可完美分类，线的内侧是一类，外侧是另一类。。

图8  

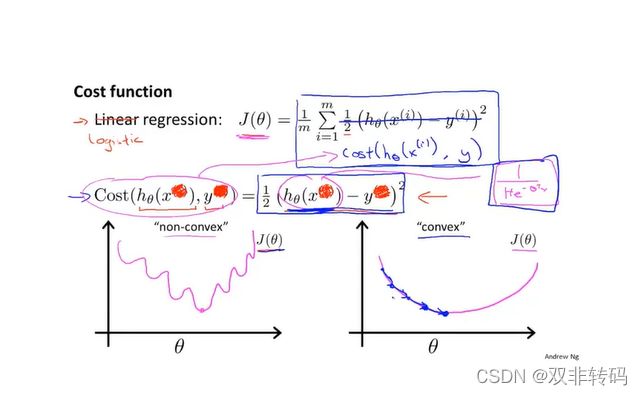
课程视频P35——代价函数

当代价函数为线性函数(Liner function), 若函数表达式中含有2次方，则容易存在代价函数图像为图9 左边那幅图像，此函数图像为非凸函数，因此在梯度下降法的迭代过程中，容易陷入局部最优解；而如果将代价函数写成log函数(Logistic function), 则代价函数图像为图9 右边那幅图像，此函数图像为凸函数，更易于使用梯度下降法迭代从而得到全局最优解。

图9  

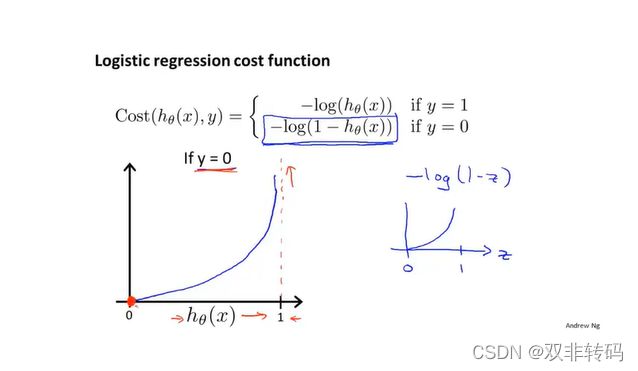
可以用$-log{h}_{\theta }(x)$和$-log(1-h_{\theta }(x))$来分别表示当真实值为y=1或y=0时的代价函数情况，如图10 图像所示，横坐标代表预测值，纵坐标代表代价函数值（可视为惩罚程度值）。此时真实值y=1的，若预测值越靠近1，说明越准确，对应的代价函数值（惩罚程度值）也越小，当预测值为1时，代价函数值（惩罚程度值）为0；若预测值越靠近0，说明越不准确，对应的代价函数值（惩罚程度值）也越大，当预测值为0时，代价函数值（惩罚程度值）为无穷大。

图10
 

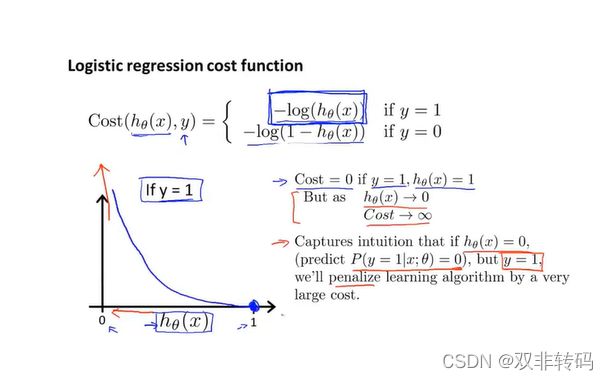
如图11图像所示，横坐标代表预测值，纵坐标代表代价函数值（可视为惩罚程度值）。此时真实值y=0的，若预测值越靠近0，说明越准确，对应的代价函数值（惩罚程度值）也越小，当预测值为0时，代价函数值（惩罚程度值）为0；若预测值越靠近0，说明越不准确，对应的代价函数值（惩罚程度值）也越大，当预测值为1时，代价函数值（惩罚程度值）为无穷大。

图11  

课程视频P36——简化代价函数和梯度下降

可以用图12所示的一个式子就同时表示了当真实值为y=1或y=0时的对应人代价函数$-log{h}_{\theta }(x)$和$-log(1-h_{\theta }(x))$情况，当y=1时，式子后半截就等于0，式子为$-log{h}_{\theta }(x)$；当y=0时，式子前半截就等于0，式子为$-log(1-h_{\theta }(x))$。
（此处主要演示手推，清晰的打印公式可见图12 ）

图12  

**图13 清晰的展示了上述公式。 **

图13  

课程视频P37——高级优化

除了梯度下降法之外，常用的还有图14 中呈现的Conjugate gradient, BFGS, L-BFGS三种方法，他们的有点是不用再手动调整并选择$\alpha$，同时收敛速度比一般的梯度下降法要更快。但是，它也存在算法过于复杂的问题，小白的话（比如在下）一般要花几个星期甚至数月去感受学习，所以就暂时不用管它，知道世界上有这么个算法就行。

图14  

图15 展示了梯度下降法求偏导时的一些编程过程。

图15  

续接上图。

图16  

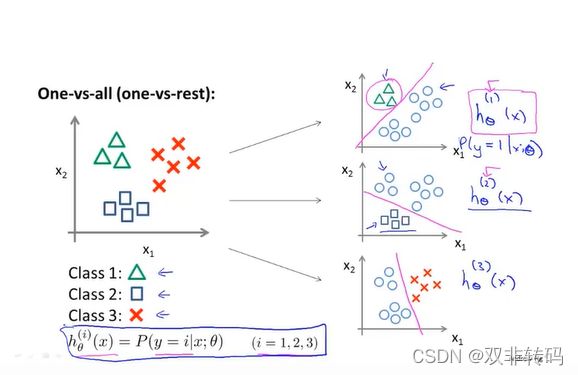
课程视频P38——多元分类：一对多

除了之前提到了二分类用0，1来表示之外，还可以用1，2，3，4…来表示具有多个特征的分类情况。

图17  

图18表示了对具有三种特征的元素进行分类的方法，选定其中一种类型元素（将其他元素看作一团），用二分类的方法从所有样本中判别出选定的那一种类型的元素；换一种选定元素，再重复以上操作三次；总共三次操作，即可完成对具有三种特征的元素进行分类。

图18  

课程视频P39——过拟合(Overfit)问题

图19 中三幅图像从左右边分别表示欠拟合(Underfit)，刚好拟合和过拟合问题(Overfit)。一般认为，欠拟合还容易解决，而过拟合是比较麻烦的问题，表现为函数过分追求与训练数据去贴合，关注了一些可能我们不看重的指标，导致泛化(generalize)性比较差，当将训练后的算法用于测试集时，表现往往不如人意。

图19  

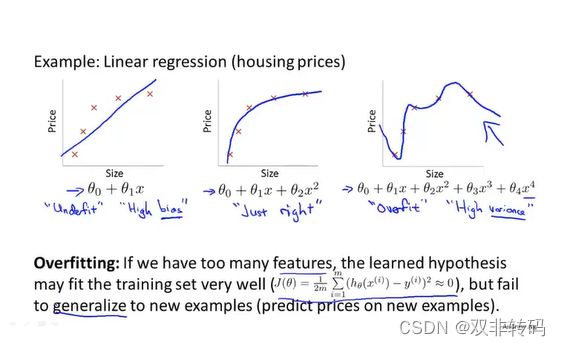
图20中三幅图像从左右边分别表示欠拟合，刚好拟合和过拟合问题。

图20  

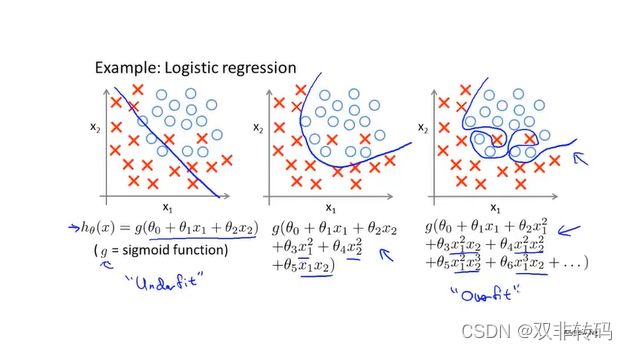
图21 形象的表现为函数过分追求与训练数据去贴合，关注了太多指标，导致泛化（generalize）性比较差。

图21  

如图22 介绍了应对函数过拟合问题的一些办法。

图22  

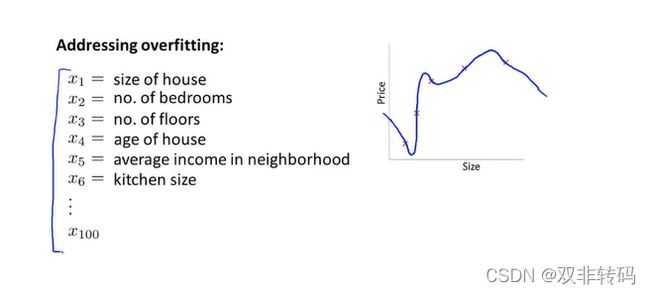
课程视频P40——代价函数

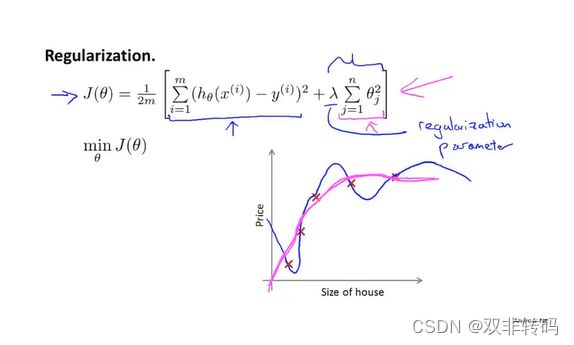
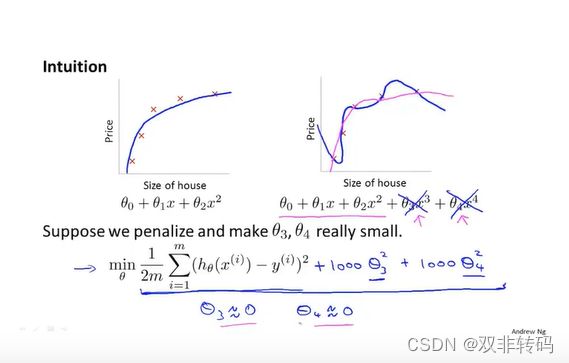
图23 介绍了“罚因子”，对于目标函数最小化问题，当某些指标对代价函数值的影响很小时，如图23 中的${\theta }_3,{\theta }_4$，我们可对其乘以一个很大的数，如此处了1000，作为代价函数的“罚因子”，当${\theta }_3,{\theta }_4$过大时，函数值将很难取得最小值，由此保证了在迭代过程中，保持${\theta }_3,{\theta }_4$的值很小。

图23  

除了“罚因子”之外，用正规化(regularization)求解时也可以对代价函数加上$\lambda ....$这一坨。

图24  

续接上图

图25  

但是$\lambda ....$的取值也不是乱取的，若$\lambda ....$取得太大了，则相当于与${\theta }_1...{\theta }_n$全都被干掉了，不起作用了，此时只剩下${\theta }_1$, 于是$h_{\theta }(x)={\theta }_1，代价函数就变成一条直线了，这样也不行。$

图26  

课程视频P41——线性回归的正则化

** 如图27表示，在梯度下降中，求偏导那一步最后加上$\frac{\lambda }{m}$${\theta }_j$, 就相当于在原来的基础上每次开头先将${\theta }_j$减去$\alpha$${\theta }_j$（一个很小的数。**

图27  

加上$\frac{\lambda }{m}$${\theta }_j$, 之后，用矩阵形式求解时的求解公式就变成了如图28所示。

图28  

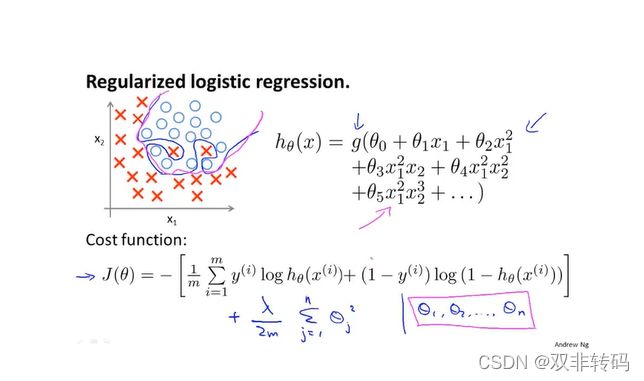
课程视频P42——Logistic回归的正则化

与线性回归的正则化类似，只是代价函数变成log函数形式了。

图29  

梯度下降法的求解也是与线性回归一样的，只是将$h_{\theta }(x)$函数换了，如图30 右下角所示。

图30  

多元函数的梯度下降法的偏导环节如下所示。

图31  

未完待续…