日常学习之：如何计算两个向量或者矩阵的余弦相似度

求向量余弦相似度的原理

余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，这就叫"余弦相似性"

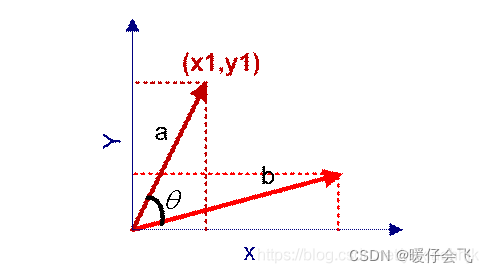
我们都学过向量的内积公式：

• 其中 $a$ 和 $b$ 可以是高维的向量，例如
  
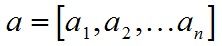
• 所以我们将向量 $a,b$ 对应位置上的数值对应相乘再相加即可得到 $a\cdot b$ 然后通过化简可以得到下面公式并求出两个 $n$ 维向量之间的夹角 $\theta$ ，而我们用这两个向量之间的 $\theta$ 角来表征这两个向量的相似程度。
  
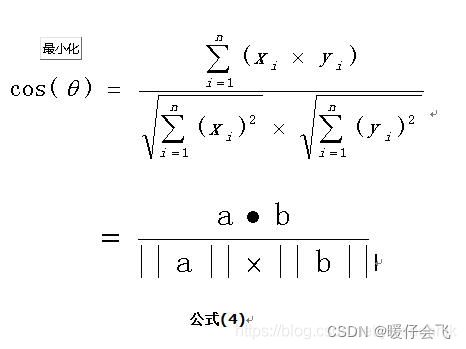
  所以我们可以很简单的写出两个向量余弦相似度的代码

import numpy as np

vec1= np.array([1,2,3,4,5])
vec2 = np.array([3,4,5,6,7])
vec3 = np.array([1,2,3,4,5])
simi12 = np.sum(vec1 * vec2) / (np.linalg.norm(vec1) * np.linalg.norm(vec2))
simi13 = np.sum(vec1 * vec3) / (np.linalg.norm(vec1) * np.linalg.norm(vec3))
print(simi12,simi13)

• 其中 np.linalg.norm() 是 np 内置的函数用来求算范数，向量的 norm1 范数就是向量的模长

矩阵的余弦相似度

相似度算法1

• 矩阵和向量的区别，就是矩阵是多个向量“拼起来” 的整体
• 假设现在有一个矩阵是 (10, 25) ，也就是 10 行 25 列，那么你可以把这个矩阵看做是，有 10 组向量，每组向量有 25 个不同的点（特征）组成，其实是把一个矩阵中的每行看做一个行向量 ，然后与另外一个矩阵（180，25）进行相似度计算的时候，其实你计算的是两个矩阵中所有的包含 25 个元素的向量的相似度是多少。
• 而计算向量相似度的方法在上面已经列出，所以我们在进行下面矩阵相似度计算的时候其实还是对其中的每个向量对应算相似度，例如 (10,25) 和 （180，25）我们需要将第二个矩阵转置成 (25,180) 然后让对应的每个向量中 25 个元素相乘再相加（即矩阵的点乘），最后除以他们模的乘积，这样可以得到每个 (25,) 维向量的相似度

$$cos(A,B)=\frac{A_{m\ast p}\cdot B_{n\ast p}^T}{|A|\cdot |B|}=\frac{A_{m\ast p}}{|A|}\cdot {\frac{B_{n\ast p}}{|B|}}^T$$

• 为了简便，可以先各自矩阵先求出每个 (25,) 向量的单位向量，再进行计算

代码演示

arr1 = np.array([[1,2,3],[4,5,6]])
arr1

array([[1, 2, 3],
       [4, 5, 6]])

arr2 = np.array([[7,8,9],[9,8,7],[0,2,5],[7,9,2]])
arr2

array([[7, 8, 9],
   [9, 8, 7],
   [0, 2, 5],
   [7, 9, 2]])

norm1 = np.linalg.norm(arr1,axis=-1,keepdims=True)
norm2 = np.linalg.norm(arr2,axis=-1,keepdims=True)
print(norm1)
print(norm2)

[[3.74165739]
 [8.77496439]]
 
[[13.92838828]
 [13.92838828]
 [ 5.38516481]
 [11.5758369 ]]

arr1_norm = arr1 / norm1
arr1_norm

array([[0.26726124, 0.53452248, 0.80178373],
   [0.45584231, 0.56980288, 0.68376346]])

arr2_norm = arr2 / norm2
arr2_norm

array([[0.50257071, 0.57436653, 0.64616234],
   [0.64616234, 0.57436653, 0.50257071],
   [0.        , 0.37139068, 0.92847669],
   [0.6047079 , 0.77748158, 0.17277369]])

cos = np.dot(arr1_norm,arr2_norm.T)
cos

array([[0.95941195, 0.88265899, 0.94295417, 0.7157235 ],
   [0.99819089, 0.96546332, 0.84647791, 0.83679902]])

• 最后得到的相似度矩阵的意义：
  • 因为 arr1 是两行，arr2 是 4 行，因此最终的输出矩阵维度是 2 行 4 列，
  • 第一行代表的是 arr1 中的第一行和 arr2 中的每一行的余弦相似度
  • 第二行代表的是 arr1 中的第二行和 arr2 中每一行的余弦相似度

场景应用

• 说了这么多，这种相似度的应用场景是什么呢？
• 人脸识别中，假设有 10 组数据，每组数据有 25 个特征点，一共构成了 (10,25) 维度的矩阵，然后现在数据库中有 (180,25) 的矩阵，即 180 组数据（180张脸），每组数据一样都是 25 个特征点，这个时候让你选出最匹配的，就要用上面这种相似度的计算方法，最后计算得出的矩阵分别是这 10组待检测的数据和 180组数据分别的匹配程度。

相似度算法2

如果我现在有两张图，每张图的大小是 (32,32)，那么我要是想通过余弦相似度计算这两张图的相似度怎么办呢？
这种情况几乎就是上面那种的特殊情况，如果你学过深度学习，你一定知道在做全连接层的时候我们需要把一个图展成一个向量，也就是说，对于这张 (32,32) 的图，我们可以把它看做一个 (1,32*32) 的向量，这个时候，如果再有一张图维度是 （32,32）也好，或者是其他的维度，我们也可以展成一个向量，然后按照向量的相似度去计算他。比如说：

代码演示

import matplotlib.pyplot as plt

train_set = torchvision.datasets.CIFAR10(root='../datasets', train=True, download=False, transform=None)

data1 = train_set.data[0]
data2 = train_set.data[1]

plt.imshow(data1)

plt.imshow(data2)

d1 = data1.ravel()
d2 = data2.ravel()
cos_simi = np.sum(d1*d2) / (np.linalg.norm(d1) * np.linalg.norm(d2))
cos_simi

0.0075490877860552525

思维扩展

想一下，如果现在给你一个包含 100 个特征图的矩阵，矩阵维度是（100,32,32,3）和另外一个包含 10 个特征图的矩阵，矩阵维度是 (10,32,32,3) 如何计算他们之间的相似度呢？

参考文献

• 使用python求两个矩阵的余弦距离

• 衡量两个向量相似度的方法：余弦相似度

• 矩阵相似度的度量方法

附：

def mtx_similar1(arr1:np.ndarray, arr2:np.ndarray) ->float:
    '''
    计算矩阵相似度的一种方法。将矩阵展平成向量，计算向量的乘积除以模长。
    注意有展平操作。
    :param arr1:矩阵1
    :param arr2:矩阵2
    :return:实际是夹角的余弦值，ret = (cos+1)/2
    '''
    farr1 = arr1.ravel()
    farr2 = arr2.ravel()
    len1 = len(farr1)
    len2 = len(farr2)
    if len1 > len2:
        farr1 = farr1[:len2]
    else:
        farr2 = farr2[:len1]

    numer = np.sum(farr1 * farr2)
    denom = np.sqrt(np.sum(farr1**2) * np.sum(farr2**2))
    similar = numer / denom # 这实际是夹角的余弦值
    return  (similar+1) / 2     # 姑且把余弦函数当线性