【自然语言处理】BOW和TF-IDF详解
BOW 和 TF-IDF 详解
机器无法处理原始形式的文本数据。我们需要将文本分解成一种易于机器阅读的数字格式(自然语言处理背后的理念!)。BOW 和 TF-IDF 都是帮助我们将文本句子转换为向量的技术。
我将用一个流行的例子来解释本文中的 Bag-of-Words(BOW)和 TF-IDF。
我们都喜欢看电影。在我决定看一部电影之前,我总是先看它的影评。我知道你们很多人也这么做!所以,我在这里用这个例子。以下是关于某部恐怖电影的评论示例:
- 评论一:This movie is very scary and long.
- 评论二:This movie is not scary and is slow.
- 评论三:This movie is spooky and good.
你可以看到关于这部电影的一些对比评论,以及电影的长度和节奏。想象一下看一千篇这样的评论是多么枯燥。显然,我们可以从中汲取很多有趣的东西,并以此为基础来衡量电影的表现。
然而,正如我们在上面看到的,我们不能简单地把这些句子交给机器学习模型,让它告诉我们一篇评论是正面的还是负面的。我们需要执行某些文本预处理步骤。
BOW 和 TF-IDF 就是两个这样做的例子。让我们详细了解一下。
1.BOW
词袋(BOW)模型是数字文本表示的最简单形式。像单词本身一样,我们可以将一个句子表示为一个词包(一个数字串)。
让我们回顾一下我们之前看到的三种类型的电影评论:
- 评论一:This movie is very scary and long.
- 评论二:This movie is not scary and is slow.
- 评论三:This movie is spooky and good.
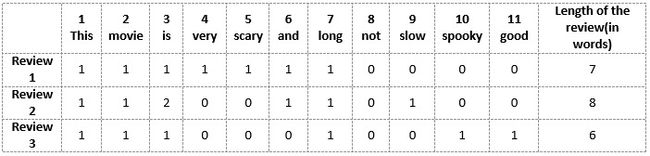
我们将首先从以上三篇评论中所有的独特词汇中构建一个词汇表。词汇表由这 11 11 11 个单词组成:“This”、“movie”、“is”、“very”、“stear”、“and”、“long”、“not”、“slow”、“spooky”、“good”。
现在,我们可以将这些单词中的每一个用 1 1 1 和 0 0 0 标记在上面的三个电影评论中。这将为我们提供三个用于三个评论的向量:
- 评论向量1:[1 1 1 1 1 1 1 0 0 0 0]
- 评论向量2:[1 1 2 0 0 1 1 0 1 0 0]
- 评论向量3:[1 1 1 0 0 0 1 0 0 1 1]
这就是词袋(BOW)模型背后的核心思想。
在上面的例子中,我们可以得到长度为 11 11 11 的向量。然而,当我们遇到新的句子时,我们开始面临一些问题:
- 如果新句子包含新词,那么我们的词汇量就会增加,因此向量的长度也会增加。
- 此外,向量还包含许多 0 0 0,从而产生稀疏矩阵(这是我们希望避免的)。
- 我们没有保留任何关于句子语法和文本中单词顺序的信息。
2.TF-IDF
TF-IDF 是一种用于信息检索与数据挖掘的常用加权技术。TF 是词频(Term Frequency),IDF 是逆文本频率指数(Inverse Document Frequency)。
评论 2 2 2: This movie is not scary and is slow.
T F ( ′ t h i s ′ ) = 评论 2 中出现 t h i s 的次数 评论 2 中的单词数 = 1 8 TF('this')=\frac{评论2中出现this的次数}{评论2中的单词数}=\frac{1}{8} TF(′this′)=评论2中的单词数评论2中出现this的次数=81
我们可以这样计算所有评论的词频:
I D F ( ′ t h i s ′ ) = l o g 文档数 包含 t h i s 一词的文档数 = l o g 3 3 = l o g ( 1 ) = 0 IDF('this')=log\frac{文档数}{包含 this 一词的文档数}=log\frac{3}{3}=log(1)=0 IDF(′this′)=log包含this一词的文档数文档数=log33=log(1)=0
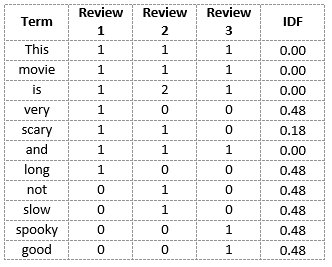
因此,我们看到 “is”、“this”、“and” 等词被降为0,代表重要性很小;而 “scary”、“long”、“good” 等词则更为重要,因而具有更高的权值。
我们现在可以计算语料库中每个单词的 TF-IDF 分数。分数越高的单词越重要,分数越低的单词越不重要: ( t f _ i d f ) t , d = t f t , d × i d f t (tf\_idf)_{t,d}=tf_{t,d}×idf_t (tf_idf)t,d=tft,d×idft T F − I D F ( ‘ t h i s ’ , R e v i e w 2 ) = T F ( ‘ t h i s ’ , R e v i e w 2 ) × I D F ( ‘ t h i s ’ ) = 1 8 × 0 = 0 TF-IDF(‘this’, Review 2) = TF(‘this’, Review 2)×IDF(‘this’) = \frac{1}{8}×0 = 0 TF−IDF(‘this’,Review2)=TF(‘this’,Review2)×IDF(‘this’)=81×0=0

我们现在已经获得了我们词汇的 TF-IDF 分数。TF-IDF 还为频率较低的单词提供较大的值,并且当 IDF 和 TF 值都较高时,该值较高。TF-IDF 分值高代表该单词在所有文档中都很少见,但在单个文档中很常见。
总结一下我们在文章中所讨论的内容:
- 词袋只创建一组向量,其中包含文档中的单词出现次数,而 TF-IDF 模型还包含关于更重要的单词和不重要的单词的信息。
- 词袋向量很容易解释。然而,在机器学习模型中,TF-IDF 通常表现得更好。
虽然 “BOW” 和 “TF-IDF” 在各自方面都很受欢迎,但在理解文字背景方面仍然存在空白。检测单词 “spooky” 和 “scary” 之间的相似性,或者将给定的文档翻译成另一种语言,需要更多关于文档的信息。
这就有关于 Word2Vec、CBOW、Skip-Gram 等词嵌入技术的由来。