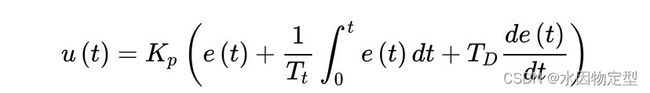我在嵌入式控制上对PID算法的理解

本文较长，目前为1.1.0版本，后续将会根据理解变化不断修改。

修改内容：

1、修改了文章错别字。

2、微控制器一般超过精度都是四舍五入而不是直接舍去。

3、叠加定理在PID上的使用我们称之为并级PID。

4、增加了大佬的指点。

———始———

理论上连续系统的 PID公式为

式中，Kp——比例增益；

Tt——积分时间常数；

TD——微分时间常数；

u(t)——PID控制器的输出信号；

e(t)——给定值与测量值之差。

式子很明显的展示了输出信号的计算公式，我们由此可知我们常用的Ki和Kd分别是Kp除以积分时间常数和Kp乘微分时间常数，所以Ki和Kd是与Kp有关的（ps : Ki=Kp/Ti Kd=Kp*Td），那么我们调参的时候需要关注这点。（ps : 我们至少采集两组数据就可以分别算出Ki、Kd和Kp之间的关系。）

这里我要先特别标注一下：Kp!=比例环，很多同学经常把Kp当成比例环，这样对PID算法的理解是不利的。

下面写一下我对各环的理解：

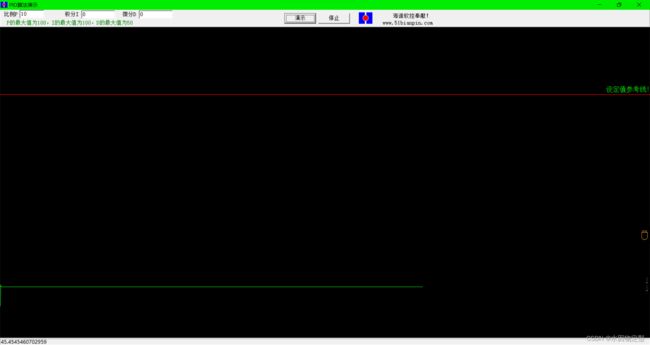
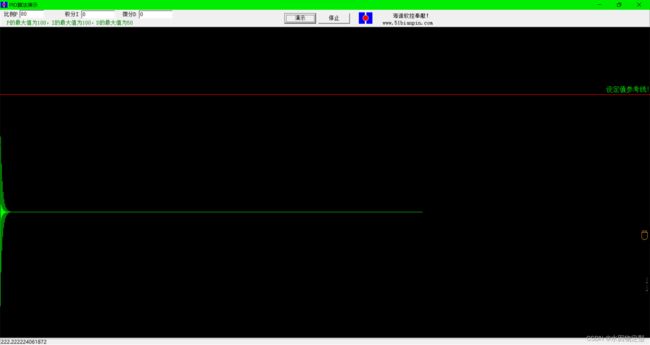
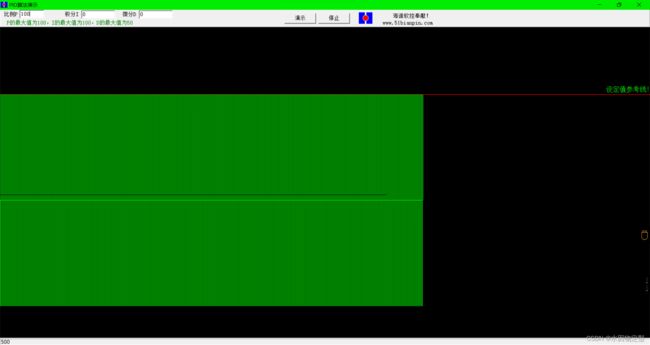
先附上几张PID的演示图片，请注意左上角的PID参数。

Kp = 10 Ki = 0 Kd = 0 

Kp = 80 Ki = 0 Kd = 0 

 Kp = 100 Ki = 0 Kd = 0

Kp = 100 Ki = 5 Kd = 0

Kp = 100 Ki = 5 Kd=1 

是不是很有趣？你或许还不能很好的理解为什么会产生这样的图像，但是你阅读完这篇文章后你一定能理解为什么曲线会是这样变化甚至能说出它们的现象的具体名称。 

比例环：比例环等于Kp*e(t)，也就是比例增益常熟乘以给定值与测量值之差。比例环在PID算法中反应是最快的，于是在需要反应速度的控制器中，Kp尤其受重视，比如：平衡小车，倒立摆，板球系统等。凡事都有两面性，比例环之所以反应速度快，是因为它能直接根据误差（我就简称给定值与测量值之差为误差了）而给出反应。就比如我们跳到某个框内，我们知道我们和框的具体距离，那么我们就可以根据距离直接跳过去。这是比例环。（ps : 积分环在这个例子中就是我们跳一次，没进框，那我们把这次误差加上之前的误差的总的和，也就是误差的总和，作为我们下一次跳的距离的参考。微分环则是，我们用上一次的与框的距离减去这一次与框的距离，也就是我们误差的变化量这里可以理解为我们跳的实际距离，作为我们下一次跳的距离的参考。）那么，如果Kp过大，很显然我们会跳过框，这就叫超调；如果下下一次跳会非常非常慢的靠近框甚至跳得更加远离框，这就叫振荡。

超调

振荡 

那么静态误差是什么呢？为什么Kp太小会出现静态误差呢？

在比例环作用下，输出信号控制结果在稳定后与实际结果存在一定误差，这就叫静态误差。

静态误差 

接着上面跳框来说，我们玩心大起，我们要用我们距离框一半的距离作为我们要跳的距离（也就是输出信号）。此时假如我们距离框有1m，那么我们第一次跳后距离框0.5m，第二次跳后距离框0.25m……第十一次跳后距离框0.00048828m。哈哈，你能跳这么小的距离吗？或许能？但是你要知道我们的微控制器都是有精度的，如果（我是说如果）你用的微控制器精度只有小数点后3位，那么你得到的结果是0.000！surprised!微控制器认为它已经在目标位置了！这是一种情况。另一种情况，我们假设微控制器和实际控制器有意识：

微控制器：兄弟，根据我的推断你需要往前跳0.00001m。

实际控制器心里：我把你当兄弟，你把我当啥了？0.00001m怎么跳？你行你来，反正我跳不了。

实际控制器回复：好的兄弟，已收到信号。

微控制器：好的兄弟，根据我的推断你需要往前跳0.00001m。

实际控制器回复：好的兄弟，已收到信号。

……

哈哈，所以它们永远到不了目标！

静态误差你理解了吗？

哦，如果你喜欢式子理解的话，你可以将误差拆开，那么公式就变为（此时不考虑积分环和微分环）：u(t)=Kp*(Target - Input)即输出信号等于 Kp乘以目标值减去输入值。当Target＝Input时（Target-Input=0，此时比例环＝0，0无意义），比例环：啥意思？我人，哦不，我环都没了你跟我说我没静态误差了？

积分环：积分环是误差对时间的积分再除以积分时间常数再乘以Kp。高数差的同学已经再瑟瑟发抖了，积分！！！好恐怖！妈妈我要回家！！哈哈，其实对于我们实际控制，PID算法输出量和输入量是离散的而不是连续的，那么积分就是简单的相加微分就是简单的相减。不可置信？但事实就是如此。在控制里面，积分很记仇！它会记住你所有与目标的距离并进行打分，比如你跳高，你跳的没目标高，NND，积分环恨铁不成钢小本本上再参上几笔+。如果你跳的比目标高，NND，积分环很厌恶你这种浪费体力的行为小本本上参上几笔-。哎，假如你天赋惊人跳的刚好，积分环就很高冷没任何反应。哈哈，懂了吧，这就是积分环的工作原理。那为什么说积分环可以消除稳态误差能？我们还是以前面的跳框为例。此时距离目标只有0.00048828m了，微控制器因为精度原因输出信号是跳0.000-24414m(-后面是因为精度而舍去的数值，后面同理，假设这个时候开始加上积分环)。这时积分环忍不了了，NND，搞我是不？参你几笔+！然后微控制器的输出信号就变成了跳0.000-24415m!在积分环的不断记仇下，输出信号终究会突破0.000m，让实际控制器产生反应！静态误差另一情况同理。当然，因为设备和计算精度等的原因，误差是永远存在的，所以我们只能说极其接近目标值可以忽略误差不记！当然，实际误差大概率比我举例的大，我说这么小只是为了方便理解。当积分作用过大后，同样会出现超调和振荡！很明显嘛，积分环的小本本上参的笔太大了以至于实际控制器反应太疯狂了！不过有一点值得肯定的是，积分环刀子嘴豆腐心，它最后的结果基本都是收敛的（如果你的实际控制器和微控制器正常的话或者说如果你的微控制器和实际控制器能在它的变化范围能正常工作的话）。

微分环：误差对时间的导数乘以微分时间常数再乘以Kp。呜呜呜，微分环一般都是扮演反派作用！所以Kd要么是负数要么它要乘个负数。前面有说微分环是根据误差的变化量来输出信号的，那么假如输出信号突然增大，微分环看着正派们洋洋得意，它很不爽：敢抢我风头？给我慢下来。于是……输出信号增量很苦逼的变小了！这样也就能解释为了微分环会拖慢反应速度但是能使输出信号更加平滑了。但是，微分环总是会慢一拍，因为它检测的是增量，那么当实际位置与目标位置很小时：

——时间段1——

微分环：你增大得太快了，你给我变慢！

输出信号：可是我现在没在变化啊！

微分环：你在质疑我？

输出信号：好吧，我负增长。

——时间段2——

微分环：嗯，不错，现在刚刚好，就保持这个势头！

输出信号：？？？行！

——时间段3——

微分环：我让你保持这个势头你怎么在负增长？

输出信号：这不是你的指令？

微分环：怎么可能！你赶紧给我停下来！

输出信号：好，好，好，你别激动！

——时间段4——

微分环：你怎么还不停，你增长太快了，给我停下来！

输出信号：可是我现在没变化啊！

微分环：你在质疑我？

输出信号：好吧，我正增长。

……

请不要将此图和“振荡图”混淆！高频低幅振荡放大后图像和振荡一样。 

微分环——昏庸的掌权者。

在我们的实际应用中，信号是离散化的，PID 通常衍生为：增量式PID和位置式PID。它们的离散公式如下。

增量式：

△u(k)= u(k)- u(k-1)；

△u(k)=Kp[e(k)-e(k-1)]+Kie(k)+Kd[e(k)-2e(k-1)+e(k-2)]；

位置式：

u(k)=Kp*e(k) +Ki* +Kd*[e(k)-e(k-1)]；

首先，我们先简单的从公式上分析，增量式的最终目标△u(k)=0也就是误差增量为0，位置式则是实际误差为0。

我们先讨论增量式。其比例环为：误差的增量乘以Kp；积分环为误差增量的的和乘以Ki（为什么说是误差增量的和？当k等于1时误差增量等于此时的误差减去上次的误差，但是k等于0时PID并未起作用，其输出信号应该是u(0)=0。也就是u初始化的值。后面的同理，[u(t-1)-u(t-2)]+[u(t)-u(t-1)]=u(t)+u(t-2)，以此递推，那么最后的结果是u(t)+u(0)即u(t)）；微分环是误差的增量的增量乘以Ki。那么在增量式PID里面，误差的增量是输入量。它和位置式里面的误差扮演着同一个角色。或许你还是不太理解，来，让我举例子具体说说。

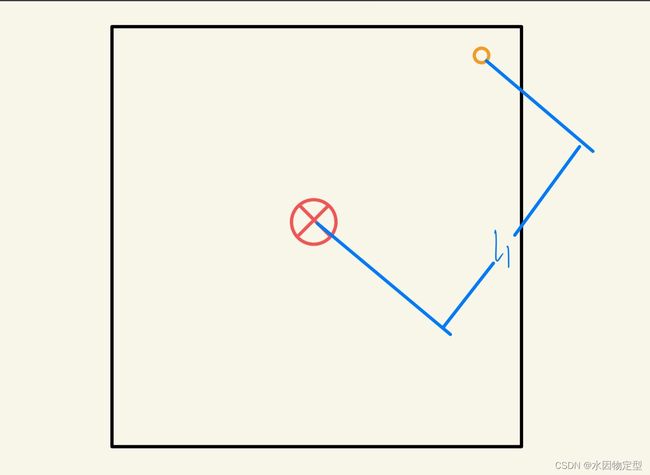
我们用增量式PID来调一个板球系统（目标是让球停在中间）如图：

那么，此时当球放下去后：

比例环的输入量等于积分环的输入量等于l1的长度;微分环输入量则是0，因为此时它只有一个值，那么它的刚刚输入参量都是初始化的值即0。

一个周期后：

比例环和微分环的输入量都为为△l；积分环的输入量为l2；

两个周期后：

比例环的输入量为△l2；积分环的输入量为l3；微分环的输入量为△l-△l2即△l'（请注意，为了方便解释△l'同意把△l2画到△l中去了）；

好了，通过这三次PID图解，你应该能理解PID各变量的作用了。那么，下面有几个问题你可以尝试回答：

1.球有没有可能停住了，但是没停在目标点？

2.如果你认为有可能出现，请简述你这样认为的理由。

3.该如何处理这个问题？

4.过度处理可能产生什么后果？

答案：

这种情况完全有可能出现！在增量式PID中唯一一个能描述球在不在目标点的只有积分环输出量！我们如果仔细观察，我们会发现，增量式PID里面的积分环不就是 PID算法中的比例环？比例环有什么必然缺点？静态误差！这个问题如果只有单级增量式 PID是无法解决的，只能通过增大Ki来缩小静态误差。如果Ki过大（也就是PID算法的Kp），那么会出现超调或者振荡。

所以呢，增量式PID更适合用去去控制变化量变化稳定。比如，让电机转速稳定（我们输入是单位时间内的脉冲即当前获取时间的总脉冲数减去上一获取时间的总脉冲数，当然，由于计算总脉冲数完全没必要所以我们实际上是从上一获取时间开始累计脉冲直到当前获取时间，而增量式PID的目的是让脉冲的增量即单位时间内的脉冲不变。这很和增量式的胃口。）

现在我们开始讨论位置式PID：其比例环输入量为误差；积分环输入量为误差的累计；微分环为误差的变化量。其各输入参数的意义和PID算法一样，我就不多赘述，因为这很PID！

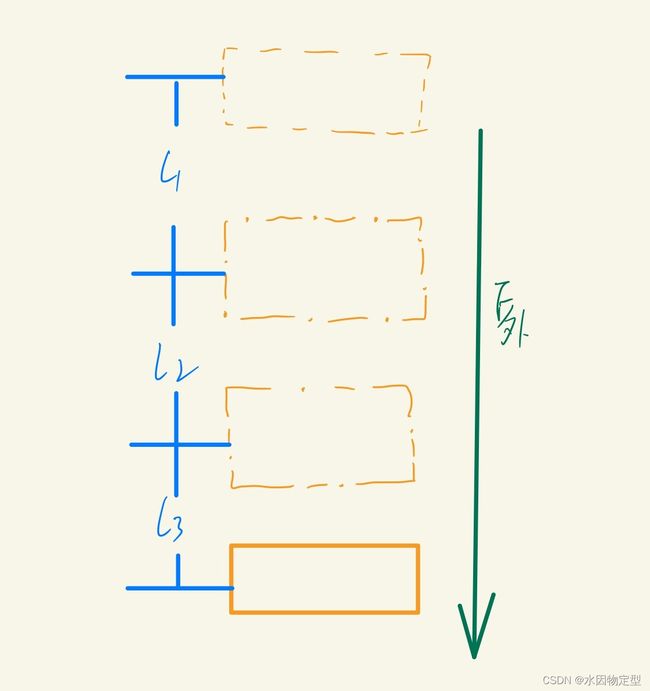
现在我们要造一辆能自动归位的平衡车。好滴，如图：

此时我们设置让平衡车原地平衡，但是小兰很顽皮，他推了一下平衡车，于是平衡车在外力作用下位移，其中l1至l3都是单位时间内的位移量，也就是每PID周期位移量。很显然的，在这张图里面从上到下位置式PID的比例环输入量分别为：0,l1,l2,l3；积分环输入量为：0,l1,l1+l2,l1+l2+l3；微分环输入量为：0,l1,l2-l1,l3-l2（实际上应该是电机的脉冲数，但是我为了方便表达，就用位移量作为脉冲数吧。因为脉冲数是和位移量线性相关的，只不过不同电机和轮胎不一样而已）。如果你在认真阅读，你会发现，积分环的输入量在不断增大！也就是说，积分环这个记仇的家伙在不断在小本本上记录小兰给他的“干扰”，伺机报复！

机会来了，当小兰松手后，积分环立马发飙，平衡车开始归位，如图：

妙吧？

不过为什么归位后不会回到原来位置？是因为微分环和比例环的作用吗？

啊哈！那不是主要原因呢。毕竟来回这两个过程比例环和微分环都有作用呢。实际上这是由于车轮打滑，编码器有误差和静态误差造成的。你问为什么有静态误差？呵呵哒，当平衡车回归时，误差总量为0就是目标值，那么每次位移误差总量都会减少，就像Kp的每次作用后与目标值误差一样。这种情况下是存在静态误差的。

所以你理解了吗？

板球系统该用什么类型的PID？

好了，相信你们都学过叠加定理。呵呵，就是线性系统的可加性！也就是说我们可以将一个问题或者现象，如果它是线性系统的话，分成多个子问题或者子现象去解决他。所以在板球系统中，我们可以在控制球停的位置上分x,y两垂直方向，当然这取决于怎么简单怎么好算。加入你的板子抬升平面并没有垂直，那么你需要换算咯，这很复杂，或许就不是线性系统了。描述物体运动通常有，位移，速度，加速度。这些是与PID的输出信号都是线性相关的吗？显然是！那么我们的叠加定理就有起作用了！嘎嘎嘎！

平衡车呢？又要让平衡车行驶，又要让他归位，又要让他平衡，叠加定理能不能用？

实际上，叠加定理在PID里的应用称为并级PID。

有一些有意思的控制器，如P-I控制器，P-D控制器等如果你能理解本文，那么也就能理解这些控制器原理。

另外感谢刘梓博学长的指点：PID控制器是不能通过超过两级的输入量来控制输出的，如果这样做那整个系统将及其不问题，如果你只是想体验或者有其它优化算法的话当我没说。

超过两级怎么理解？就比如：位移和速度之间差了一级，而位移和加速度之间差了两级。（速度是位移对于时间的微分，加速度是位移对于时间的微分的微分）

———终———

新手上路，有哪里写的不好的地方请各位大佬斧正。

附：

文章开头的PID演示软件：

链接：https://pan.baidu.com/s/13o0gIoVgZSf6b3EOEq76gA 
提取码：1701