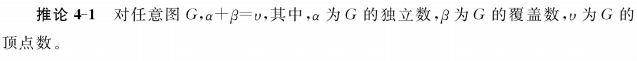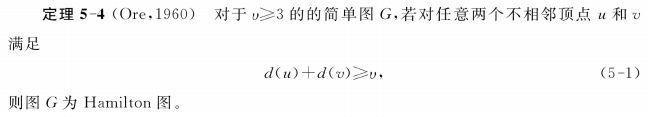图论相关概念及术语总结

前言：本文主要从数学角度，简单介绍了图论中的一些概念与术语，主要基于教材《图论及其应用》(北京邮电大学出版社)的前6章内容，如有错误，诚请指正

---

1.图的概念

1.1 图的定义

1.1.1 无向图相关定义

    顶点集/节点集：

        

            其中每个元素称为图G的一个顶点/节点

    边集：

         

            其中每个元素 是图G的一条边

    图：

        

            其中V(G)为顶点集，E(G)为边集合

1.1.2 有向图相关定义

    弧集：

         

            其中每个元素 为从 到 的一条弧

    弧相关概念：

        

        弧：ab，称为一条弧

        头：b，为弧ab的头

        尾：a，为弧ab的尾

        出弧：对a，弧ab是出弧

        入弧：对b，弧ab是入弧

    有向图：

        

            其中V(D)为顶点集，A(D)为弧集

    基础图：

        对于有向图，去掉弧的方向，端点不变，即得到基础图；有向图去掉方向

    定向图：

        对于无向图，为每条边指定一个方向，即得到定向图；无向图加方向

 

1.2 图的基本概念

1.2.1 基本概念

    阶：图G中顶点个数

            或   

    关联：

        

            边ab与顶点a/b相关联，顶点a/b与边ab相关联

    相邻：

        

            a与b相邻；a是b的邻点/邻居

    内/外邻点：

        

            a为b的内邻点；b为a的外邻点

            对于一个点，所有指向其的点为内邻点，所有由其指出的点为外邻点

    端点：

        

            a与b是ab的两个端点

    环：

        

            k是一个环，其两端点相同

    棱：

        

            边ab是一条棱，其两端点不同

    孤立点：

        不与任何顶点相邻的顶点

    重边/平行边：

        

            边p与边q是重边

    重弧：

        

        弧p与弧q是重弧，其端点相同且方向一致

    邻域： 

        

            即图中与u相邻的点构成的集合

    内/外邻域：

        内邻域： ，即v的所有内邻点构成的集合

        外邻域： ，即v的所有外邻点构成的集合

    独立集：

         中任意两个顶点在图G中互不相邻，则称V'为图G的独立集

1.2.2 常见图定义

    简单图：无环、无重边的图

    平凡图：仅有一个顶点的图(可有多条环)

    空图/零图：没有边的图

    有限图：顶点数与边数都是有限的图

    严格有向图：无环、无重弧的图

1.2.3 度相关概念

无向图：

    度： ，顶点v所关联的边的数目(环计两次)

    奇点：度为奇数的点

    偶点：度为偶数的点

    悬挂点/叶点：度为1的点

    孤立点：度为0的点

    最大度：

    最小度：

有向图：

    出度： ，即点v出弧的数目

    入度： ，即点v入弧的数目

    最大出度：

    最大入度：

    最小出度：

    最小入度：

    源点： ，即入度为0的点

    汇点： ，即出度为0的点

 

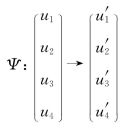
1.3 同构与恒等

    恒等：两图的顶点集与边集完全相同

        

        例：

            

                G与H恒等，与F不恒等

 

    同构：两图的顶点集存在某种映射，边集也存在某种映射，使其能一一对应

        

        例：

            

                G、H、F三者同构

            证明：G与H同构

                对于点集，可以找到如下映射

                    

                对于边集，可以找到如下映射

                    

                能够使两图一一对应，因此同构

 

1.4 完全图

    完全图：

        定义：图中任意两点间都有边相连，记作

        例：

            

    偶图/二分图/二部图：

        定义：顶点集可划分X与Y两不相交非空子集，对于每条边，都有一个顶点在X中，另一个顶点在Y中；记作G=(X,Y;E)

        例：

            

    完全偶图/完全二分图/完全二部图：

        定义：X与Y中任意两点都有唯一边相连

        例：

            

 

1.5 子图

1.5.1 基本概念

    子图：若且，则称H是G的子图，记作

    母图：若 ，则称G是H的母图

    真子图：若 且 ，则称H是G的真子图

    生成子图：若 且 ，则称H是G的生成子图

    点导出子图：

        定义：若  (即以V'为顶点集，V'中所有边为边集)，则 称为G的点导出子图

        例：

            

    边导出子图：

        定义：若(即以E'为边集，E'中所有端点为点集)，则 称为G的边导出子图

        例：

            

    基础简单图：从图G中去掉所有重边和环后所得的简单图，称为图G的基础简单图

 

1.5.2 图的基本运算

    点减法：

        定义：

            

    边减法：

        定义：

            

            

        例：

            

    并：

    交： 

 

1.5.3 其他概念

    不相交：若 ，则称G1与G2为不相交的

    边不相交：若 ，则称G1与G2为边不相交的         

    联图：对于两不相交的图 和 的并图 ，连接 与 中每对顶点所得到的图，称为图与的联图，记作

    k-正则图：

        定义：无向图G中的每个顶点的度数都是常数k，则称为k-正则图

        例：

            

    补图：

        定义：

        例：

            

    极大子图：图G的子图H具有性质P，若不存在具有性质P的子图F，使得 ，则称H为图G的具有性质P的极大子图

    极小子图：图G的子图H具有性质P，对任意的具有性质P的子图F，使得 ，则称H为图G的具有性质P的极小子图

    线图/边图：以图G的边集E(G)作为顶点集合，两顶点相邻的充要条件是这两顶点在图G中是相邻的边

 

1.6 路与连通

1.6.1 路及相关概念

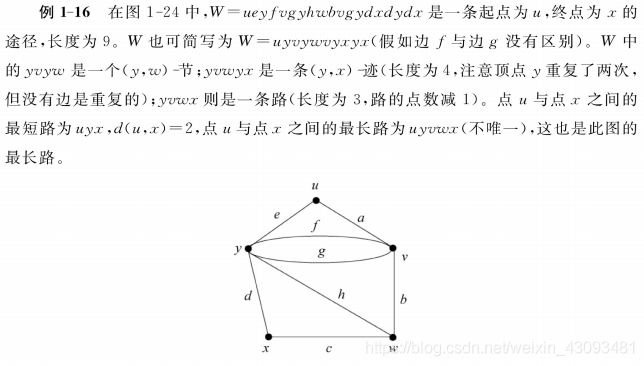
    途径： 图G中一个顶点与边交替出现的有限非空序列，；不引起混淆时可简化，将其中的边去掉

        起点：

        终点：

        内部顶点：

        长：途径W的边数k

        节/段：途径W上任意连续一段

        逆途径：将起点与终点调换得到的逆向序列，记作

        衔接：若途径W的终点是途径W'的起点，则可将其衔接，记作WW'

    迹：边互不相同的途径(点可重复)

        迹长：迹上的边数

    路：顶点互不相同的途径(边可重复)

        路长：路上的边数

    最长路：对于(u,v)两点间，边数最多的路

    最短路：对于(u,v)两点间，边数最少的路

    距离：(u,v)两点的最短路，即u与v的距离

    例子：

        

1.6.2 连通的相关概念

    连通：u与v之间有路

    连通图：图中任意两点间都有路

    连通分支：

        定义：

 

        例：连通分支数为3

            

    直径： ，即图中最长的最短路

    边割/割集：

        即为边割

    可达：有向图D中，存在从u到v的路，则称v为从u可达的

    双向连通：若u与v相互可达，则称u与v双向连通

    竞赛图：完全图的定向图

 

1.7 圈

    闭途径：起点与终点相同且长度大于0的途径

    闭迹/回路：起点与终点相同的迹

    圈：起点与终点相同的路

    闭途径/闭迹/圈的长度：包含边的个数

    奇/偶圈：长度为奇数/偶数的圈

    k-圈：长度为k的圈

    圈长：最短圈的长度

    周长：最长圈的长度

    Hamilton圈：图中所有顶点都在圈上

    例：

     

---

2.树与最优树

2.1 树的概念

    森林：不含圈的图

    树：连通的无圈图

    割边： 若e使得 ，则称e为图G的割边；即去掉该边，使得图的连通分支数减小

    非割边：若e使得 ，则称e为图G的非割边

    树叶：树中度为1的顶点

    割点：

        

            若图G的边集E(G)可分为两非空子集 和 ，使得 ,则称v为图G的割点

    偏心率： ，即v点到距其最远的顶点w之间的距离

    中心：偏心率最小的顶点

    半径： ，即中心点的偏心率

    直径： ，即图G的最大偏心率

 

2.2 树的性质

若G为树，则以下定义等价：

 

2.3 生成树

    生成树：一棵树T如果是连通图G的生成子图，则称树T为图G的生成树

    最优生成树：所有生成树中权值合最小的一个

    关联边割： ，即图G中所有与顶点v相关联的边的集合

    键：使得  的极小边集B，称为图G的键

    例：

        

    补图： ，为图G中图H的补图

    余树：当T为图G的生成树时，称 为图G的余数

        

---

3.匹配与覆盖

3.1 匹配

    匹配：图G的一个边子集M中，每条边两个端点不同，且任意两条边互不相邻，则称M为G的一个匹配

    相匹配：若边 ，则称点u与点v在M下相匹配

    M-饱和：若边 ，则称点u与点v为M-饱和的

    M-不饱和：若点u所有相关联的边都不属于一个匹配M，则称u为M-不饱和的

    完美匹配：图G中每一个顶点都被一个匹配M所饱和

    最大匹配：对任意匹配M'，都有 ，则称M为最大匹配

    完全匹配：偶图中的完美匹配

    邻集：N(S)，图中所有与S中顶点相邻的顶点集合

    1-因子：完美匹配M的边导出子图G[M],称为G的1-因子

    M-交错路：对于图G的一个匹配M，P是图G中一条路，若P的边交替属于M和E(G)\M，则称路P为图G的M-交错路

    M-可扩路：若交错路P的起点与终点都是M-不饱和的，则称P为图G的M-可扩路

    奇分支：顶点数为奇数的分支

    偶分支：顶点数为偶数的分支

    例：

        

 

3.2 覆盖

    例图：

        

    独立集：图G的顶点子集V'中任意两个顶点在图G中互不相邻，则称V'是图G的独立集；其导出子图G[V']为空图

        例：V'={v1,v5}是独立集，因为v1与v5不相邻

    团：图G的顶点子集S中任意两个顶点在图G中都相邻，则称S为图G的团；其导出子图G[S]为完全图

    覆盖：对于图G的顶点子集K，若图G的每条边中至少有一个端点在K中，则称K为图G的覆盖；其导出子图G[V\K]为空图或V\K为独立集

        例：K={v1,v3,v5,v7}是一个覆盖，因为任找一条边，一定有一个端点属于K

    最大独立集：顶点数最多的独立集

        独立数：最大独立集的顶点数，记作α(G)

        例：{v2,v4,v7}为最大独立集，独立数α=3

    最小覆盖：顶点数最少的覆盖

        覆盖数：最小覆盖的顶点数，记作β(G)

        例：{v1,v3,v5,v7}为最小覆盖，β=4

---

4.遍历问题

4.1 Euler图

    环游：通过图中每条边至少一次的闭途径

    Euler环游：通过图中每条边恰一次的闭途径

    Euler迹：通过图中每条边的迹 / 通过图中每条边恰一次的途径(一笔画)

    Euler图：包含Euler环游的图

        例：Ae1Be3Ce4Be2A 为Euler环游

            

    充要条件：图G为Euler图的 <=> 图G中所有点的度数为偶数

 

4.2 Hamilton图

    Hamilton路：通过图中每个顶点的路 = 生成路

    Hamilton圈：通过图中每个顶点的圈 = 生成圈

    Hamilton图：包含Hamilton圈的图

        例：

            

    闭包：

        定义：图G的简单生成母图，即由G开始，通过反复将其中不相邻且度之和大于等等于v的顶点用新边相连，直到不能继续为止，记作c(G)

        例：后图为前图闭包

            

---

5.网络流

5.1 网络及相关概念

    网络：N=(X,Y,I,A,c)为一个网络，当：

        (1)D=(V,A)是一个有向图

        (2)c是A上的非负函数

        (3)X与Y是两个非空不相交子集，其余顶点集合为I

    发点集合/源点集合：N中的X

        发点/源点：X中的顶点

    收点集合/宿点集合：N中的Y

        收点/宿点：Y中的顶点

    中间点集合：N中的I

        中间顶点：I中的顶点

    容量函数：N中的c

        容量：c(a)的值

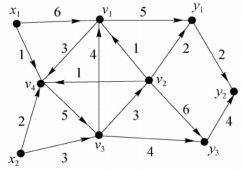
    例：

        其中N=(X,Y,I,A,c)，X={x1,x2}，Y={y1,y2,y3}，I={v1,v2,v3,v4}，各容量为边权值

        

 

5.2 流及相关概念

    流：定义在N=(X,Y,I,A,c)上的的整数函数f(.)为流，当：

        (1)容量约束条件：

        (2)守恒条件：

    流量：f(a)为弧a上的流量

    零流：f(a)=0

    合成流出流量(流出净流量)：

    合成流入流量(流入净流量)：

    流值：

        例：val f = 6

            

 

5.3 最大流

    最大流：若不存在 (.)，使得 ，则称 (.)为最大流

    割：对网络N=(x,y,I,A,c)，和V(N)的一个顶点子集S，若 ，则称为网络N中的割

    容量： 

        

    最小割：对网络中的一个割K'，若对任意割K都有 ,则称K'为网络N的最小割

    对弧a：

        f-零的：f(a)=0

        f-正的：f(a)>0

        f-不饱和的：f(a)

        f-饱和的：f(a)=c(a)

    对路p：

        

        f-饱和的：l(P)=0

        f-不饱和的：l(P)>0

        f-可增路：P是以x为起点，以y为终点的f-不饱和路

    修改流：

        

        称f'为网络N基于P的修改流

---

附录

常见定理总结

 

第一章：

    

    

    

    

    

    

    

    对于k-边连通图G，有ε>=kn/2

---

第三章：

    

    

    一颗树Δ>=k，则其中至少有k个度为1的顶点

---

第四章：

      

---

第五章：