【人工智能原理自学】深度学习：神奇的DeepLearning

你好，我是小航，一个正在变秃、变强的文艺倾年。
笔记来自B站UP主Ele实验室的《小白也能听懂的人工智能原理》。
本文讲解深度学习：神奇的DeepLearning，一起卷起来叭！

一、“调参”

今天我们以著名的Tensorflow游乐场为例，体验“调参侠”的“快乐”！
参考链接：Tensflow游乐场

码住，我们先了解一下网站是干嘛的：

我们先选择第三个数据集，调参模拟训练一下：

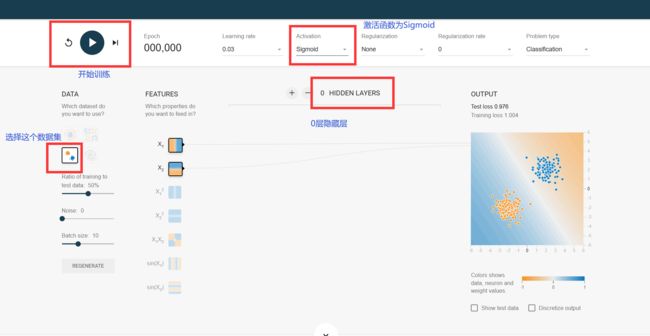
训练结果：

我们再试一个圈圈数据集：

我们思考，它需要几个神经元呢？
我们定性分析一下，还是看图说话，一个神经元是一条直线，三个神经元形成三条直线刚好形成闭合的形状。

如此看来，我们需要三个神经元作为一层隐藏层，然后把三个神经元的计算结果通过一个输出层神经元汇合，通过sigmoid函数修饰一下，就可以了。

果然，最后的输出结果：等高线完美的分割了这两类豆豆

我们再来试试第二个数据集：
这个数据集其实是感知器最初发展阶段，困扰研究人员很多年的一个问题：

但现在我们知道只需要三个神经元即可分割：

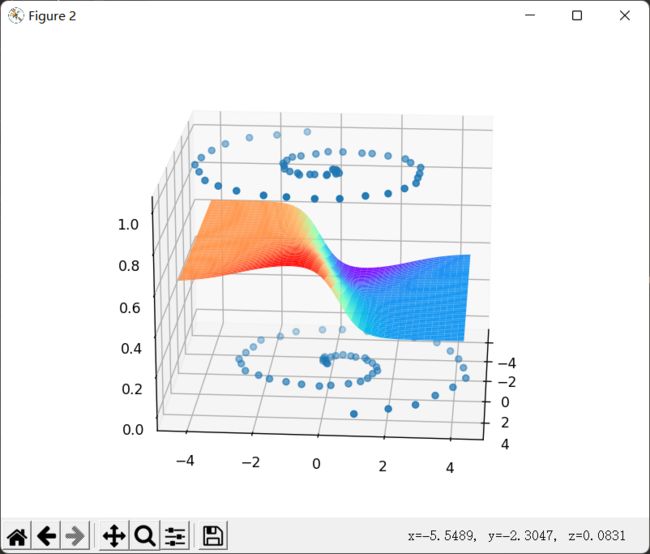
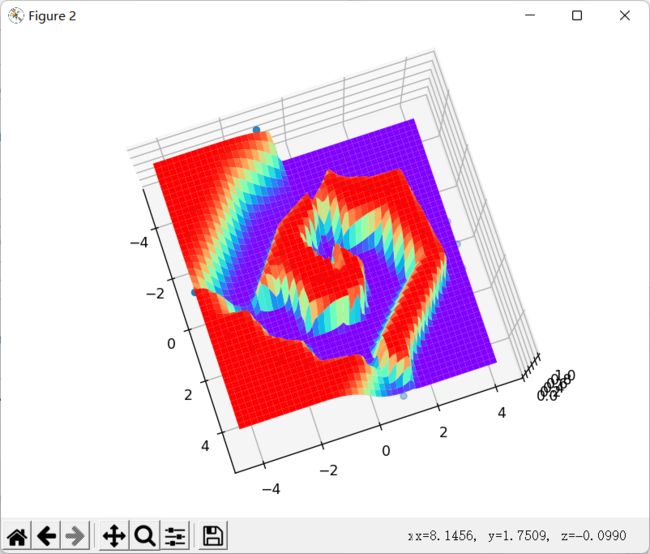
我们再来看最后一个蚊香一样的螺旋形数据集：

很明显，只有一层三个神经元的隐藏层的神经网络，在这种复杂的数据集上表现十分疲软，那我们就用更深、神经元数量也更多的网络来尝试一下。

我们增加到三层隐藏层，每层有四个神经元：

然而训练结果，动也不动，这是因为我们的老伙计“sigmoid”激活函数的问题。

我们之前说过之所以选择sigmoid函数作为激活函数，那是因为相比于阶跃函数处处可导，且导数处处不为0，这样我们反向传播算法，梯度下降求导很是方便

但我们发现一旦原离中心点，虽然仍旧可导，导数不为0，但是导数却及其的小，这样梯度下降就很难进行。

所以我们一般使用relu算法：

一半很难遇到折点，如果真遇到了，那就特殊处理一下叭。
如果陷入z<0的部分，很有可能导致这个神经元死亡，也就是死亡Relu问题（根据求导链式法则，如果激活函数求导为0那就锁定了这个神经元的参数梯度为0，权重将无法更新）

所以人们又提出了一种改进版的Relu函数：

不过梯度消失不止与激活函数有关，还有其他因素有关，目前也有很多相关的研究，但按照经验使用relu激活函数都会有不错的效果。

我们把激活函数改为Relu函数，再试一次：

咦，似乎有了点效果，我们把每层的神经元增加到8个：

嗯，效果好了不少！

二、“炼丹”

我们对上述过程代码实现：

豆豆数据集模拟：dataset.py

import numpy as np
import random

def get_beans(counts):
	posX,posY = genSpiral(int(counts/2),0,1)
	negX,negY = genSpiral(int(counts/2),np.pi,0)
	X = np.vstack((posX,negX))
	Y = np.hstack((posY,negY))
	return X,Y

def genSpiral(counts,deltaT, label):
	X = np.zeros((counts,2))
	Y = np.zeros(counts)
	for i in range(counts):
		r = i / counts * 5
		t = 1.75 * i / counts * 2 * np.pi + deltaT;
		x1 = r * np.sin(t) + random.uniform(-0.1,0.1)
		x2 = r * np.cos(t) + random.uniform(-0.1,0.1)
		X[i] = np.array([x1,x2])
		Y[i] = label
	return X,Y 

def dist(a, b):
	dx = a['x'] - b['x'];
	dy = a['y']- b['y'];
	return np.sqrt(dx * dx + dy * dy);
def getCircleLabel(p, center):
	radius = 1;
	if dist(p, center) < (radius * 0.5):
		return 1
	else:
		return 0

def randUniform(a=-1, b=1):
  return np.random.rand() * (b - a) + a;

def classifyCircleData(numSamples=100, noise=0):
	points = [];
	Y = []
	X = []
	radius = 1;
	num = int(numSamples/2)
	for i in range(num):
		r = randUniform(0, radius * 0.5);
		angle = randUniform(0, 2 * np.pi);
		x = r * np.sin(angle);
		y = r * np.cos(angle);
		noiseX = randUniform(-radius, radius) * noise;
		noiseY = randUniform(-radius, radius) * noise;
		label = getCircleLabel({'x': x + noiseX, 'y': y + noiseY}, {'x': 0, 'y': 0});
		X.append([x+1,y+1])
		Y.append(label)
  

	for i in range(num):
		r = randUniform(radius * 0.7, radius);
		angle = randUniform(0, 2 * np.pi);
		x = r * np.sin(angle);
		y = r * np.cos(angle);
		noiseX = randUniform(-radius, radius) * noise;
		noiseY = randUniform(-radius, radius) * noise;
		label = getCircleLabel({'x': x + noiseX, 'y': y + noiseY}, {'x': 0, 'y': 0});
		X.append([x+1,y+1])
		Y.append(label)

	X = np.array(X)
	Y = np.array(Y)

	return X,Y

豆豆毒性分布如下：

绘图工具：plot_utils.py

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
from keras.models import Sequential#导入keras


def show_scatter_curve(X,Y,pres):
	plt.scatter(X, Y) 
	plt.plot(X, pres) 
	plt.show()

def show_scatter(X,Y):
	if X.ndim>1:
		show_3d_scatter(X,Y)
	else:
		plt.scatter(X, Y) 
		plt.show()


def show_3d_scatter(X,Y):
	x = X[:,0]
	z = X[:,1]
	fig = plt.figure()
	ax = Axes3D(fig)
	ax.scatter(x, z, Y)
	plt.show()

def show_surface(x,z,forward_propgation):
	x = np.arange(np.min(x),np.max(x),0.1)
	z = np.arange(np.min(z),np.max(z),0.1)
	x,z = np.meshgrid(x,z)
	y = forward_propgation(X)
	fig = plt.figure()
	ax = Axes3D(fig)
	ax.plot_surface(x, z, y, cmap='rainbow')
	plt.show()



def show_scatter_surface(X,Y,forward_propgation):
	if type(forward_propgation) == Sequential:
		show_scatter_surface_with_model(X,Y,forward_propgation)
		return
	x = X[:,0]
	z = X[:,1]
	y = Y

	fig = plt.figure()
	ax = Axes3D(fig)
	ax.scatter(x, z, y)

	x = np.arange(np.min(x),np.max(x),0.1)
	z = np.arange(np.min(z),np.max(z),0.1)
	x,z = np.meshgrid(x,z)

	X = np.column_stack((x[0],z[0]))
	for j in range(z.shape[0]):
		if j == 0:
			continue
		X = np.vstack((X,np.column_stack((x[0],z[j]))))

	print(X.shape)
	r = forward_propgation(X)
	y = r[0]
	if type(r) == np.ndarray:
		y = r

	
	y = np.array([y])
	y = y.reshape(x.shape[0],z.shape[1])
	ax.plot_surface(x, z, y, cmap='rainbow')
	plt.show()

def show_scatter_surface_with_model(X,Y,model):
	#model.predict(X)

	x = X[:,0]
	z = X[:,1]
	y = Y

	fig = plt.figure()
	ax = Axes3D(fig)
	ax.scatter(x, z, y)

	x = np.arange(np.min(x),np.max(x),0.1)
	z = np.arange(np.min(z),np.max(z),0.1)
	x,z = np.meshgrid(x,z)



	X = np.column_stack((x[0],z[0]))

	for j in range(z.shape[0]):
		if j == 0:
			continue
		X = np.vstack((X,np.column_stack((x[0],z[j]))))

	print(X.shape)
	y = model.predict(X)
	
	# return
	# y = model.predcit(X)
	y = np.array([y])
	y = y.reshape(x.shape[0],z.shape[1])
	ax.plot_surface(x, z, y, cmap='rainbow')
	plt.show()

def pre(X,Y,model):
	model.predict(X)

梯度下降：beans_predict.py

import dataset
import plot_utils
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD

m = 100
X, Y = dataset.get_beans(m)
plot_utils.show_scatter(X, Y)

model = Sequential()

model.add(Dense(units=8, activation='relu', input_dim=2))
model.add(Dense(units=8, activation='relu'))
model.add(Dense(units=8, activation='relu'))
model.add(Dense(units=1, activation='sigmoid'))

model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.05), metrics=['accuracy'])
model.fit(X, Y, epochs=5000, batch_size=10)

pres = model.predict(X)

plot_utils.show_scatter_surface(X, Y, model)

训练前：

训练后：

 [ 笔者 ]   文艺倾年
 [ 更新 ]   2023.1.19
❌ [ 勘误 ]   /* 暂无 */
 [ 声明 ]   由于作者水平有限，本文有错误和不准确之处在所难免，
              本人也很想知道这些错误，恳望读者批评指正！
 [ 代码 ]   https://github.com/itxaiohanglover/ai_lesson