吴恩达【深度学习】笔记01——向量化、For循环及Python中的Broadcasting

向量化是非常基础的去除代码中for循环的艺术，在深度学习安全领域、深度学习实践中，你会经常发现自己训练大数据集，因为深度学习算法处理大数据集效果很棒，所以代码的运行速度非常重要。否则在数据集很大时，代码需要花费很长时间去处理。在深度学习领域，运行向量化是一个关键的技巧。

1. 向量化

举一个例子说明什么是向量化：

在逻辑回归中需要计算 $z=w^{T}x+b$ 。其中 $w$ 和 $x$ 都是列向量。如果样本有很多特征，那么该列向量将会非常大。如果使用的是非向量化方法去计算该式，则代码如下：

z=0
for i in range(n_x):
  z+=w[i]*x[i]
z+=b

这是一个非向量化的实现，你会发现这真的很慢，作为一个对比，向量化实现将会直接计算 $w^{T}x$，其代码如下：

z=np.dot(w,x)+b

这是向量化的实现方法，你将会发现这个非常快。为了更加直观的对比向量化实现方法与非向量化实现方法的运行速度，在jupyter中输入以下示例：

import numpy as np
a=np.array([1,2,3,4])
a  # array([1, 2, 3, 4])

2. 向量化实现

在下例中，通过random随机得到两个一百万维的数组，并记录下在实现向量化之前以及之后的时间，相减得到运行时间：

import time
a=np.random.rand(1000000)  # 通过random随机得到两个一百万维的数组
b=np.random.rand(1000000)
tic=time.time()  # 测量当前的时间
c=np.dot(a,b)  # 使用向量化实现
toc=time.time()  # 测量使用向量化实现所花费的时间
print("向量化方法的运行结果为：" + str(c))
print("Vectorized version:"+str(1000*(toc-tic))+"ms")

向量化实现的结果为：

3. 非向量化实现

非向量化版本的for循环花费的时间如下：

c=0
tic=time.time()
for i in range(1000000):
    c += a[i]*b[i]
toc=time.time()
print("非向量化方法的运行结果为：" + str(c))
print("For Loop:"+str(1000*(toc-tic))+"ms")

其运行结果为：

【总结】在向量化和非向量化方法中，得到了相同的c。如你所见，向量化版本花费了1.5毫秒，非向量化版本的for循环花费了大约656毫秒。非向量化版本多花费了400倍的时间。仅仅是在这一个小例子中，只需向量化代码，速度就可以提升近400倍。

一句话总结，无论什么时候，避免使用明确的for循环。

当你想写循环的时候，检查numpy是否存在类似的内置函数，从而避免使用循环方式。
【例】已知 $v$ 向量，求关于 $v$ 向量指数级的向量 $u$ 。 $v$ = $\left[\begin{array}{c}{v}_1\\ v_2\\ ...\\ v_n\end{array}\right]$
若使用非向量化版本的for循环，则代码如下：

u=np.zeros((n,1))  # 初始化n*1维向量
for i in range(n):
  u[i]=math.exp(v[i])

若使用向量化版本，则只需两句代码：

import numpy as np
u=np.exp(v)

通过之前的实验，我们知道向量化版本效率明显快于循环方式。
事实上，numpy库中有很多向量函数。比如u=np.log()是计算对数函数，np.abs()是计算数据的绝对值，np.maxinum(y)是计算元素y中的最大值……

4. python中的广播

在向量化逻辑回归中，numpy命令是Z = np.dot(w.T, X) + b。这里的b是一个实数或者可说成一个1×1的矩阵。但是当你将前面的向量加上这个实数时，Python自动的把这个实数扩展成一个1×m的行向量。这就是Python中的广播。

【例】下面列表是不同食物（每100g）中不同营养成分的卡路里含量表格，表格为3行4列，列表示不同的食物种类，从左至右依次为苹果，牛肉，鸡蛋，土豆。行表示不同的营养成分，从上到下依次为碳水化合物，蛋白质，脂肪。那么，我们现在想要计算不同食物中不同营养成分中的卡路里百分比。

计算苹果中的碳水化合物卡路里百分比含量，首先计算苹果（100g）中三种营养成分卡路里总和=56+1.2+1.8=59，然后用56/59=94.9%算出结果。对于其他食物，计算方法类似。

首先，按列求和，计算每种食物中（100g）三种营养成分总和，然后分别用不同营养成分的卡路里数量除以总和，计算百分比。

那么，能否不使用for循环完成这样一个计算过程呢？

假设上图的表格是一个3行4列的矩阵，接下来我们要用Python的numpy库完成这样的计算。在Jupyter notebook中输入数据：

import numpy as np

A = np.array([[56.0, 0.0, 4.4, 68.0],
             [1.2, 104.0, 52.0, 8.0],
             [1.8, 135.0, 99.0, 0.9]])
print(A)

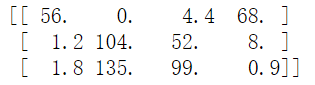
利用axis=0来计算每一列的和。axis用来指明将要进行的运算是沿着哪个轴执行，在numpy中，0轴是垂直的，也就是列。而1轴是水平的，也就是行。

cal = A.sum(axis=0)  # 按列求和
print(cal)  # [ 59.  239.  155.4  76.9]

接下来计算百分比，这条指令将3×4的矩阵A除以一个1×4的矩阵，得到了一个3×4的结果矩阵，这个结果矩阵就是我们要求的百分比含量。

per = A/cal.reshape(1,4)
print(per)

A/cal.reshape(1,4)指令调用了numpy中的广播机制。技术上来说，其实不需要再将矩阵cal重塑（reshape）成1×4的矩阵，因为cal本身就是1×4的矩阵。但是当我们写代码不确定矩阵维度的时候，通常会对矩阵进行重塑来确保得到我们想要的列向量或行向量。

【例】用一个2×3的矩阵和一个1×3的矩阵相加。

其泛化形式是 m×n 的矩阵和 1×n 的矩阵相加。在执行加法操作时，其实是将 1×n 的矩阵复制称为 m×n 的矩阵，然后两者做逐元素加法得到结果。（注：广播机制与执行的运算种类无关，即它也适用于除法操作）

【例】用一个2×3的矩阵和一个2×1的矩阵相加。

这里相当于是一个 m×n 的矩阵加上一个 m×1 的矩阵。在进行运算时，会先将 m×1 的矩阵水平复制n次，变成一个 m×n 的矩阵，然后再执行逐元素加法。

【总结】对于不同维度的矩阵做加四则运算，python会自动展开低维矩阵，使其跟高维矩阵同维，然后再做四则运算。

5. 补充：关于numpy中向量的说明

为了演示Python-numpy中一个容易被忽略的效果，这里举一个简单的例子。

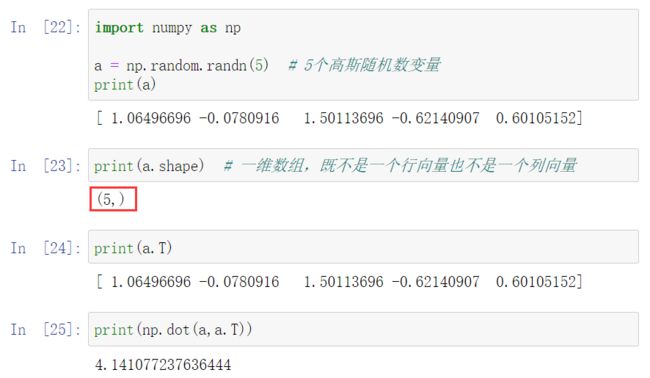
由上述代码可知，此时的a的shape是一个(5,)的结构。这在Python中被称作一个一维数组。它既不是一个行向量也不是一个列向量，这也导致它有一些不是很直观的效果。 上述例子中，我想要输出a的转置矩阵，但是输出的结果与a看起来并无差别。所以，当你在编程练习或者在执行逻辑回归和神经网络时，你不需要使用这些一维数组。

解决该问题的方法很简单，只需要将其定义为一个行向量或者列向量即可。关于向量的一些行为会更容易被理解。

注意一个细微点，在这种数据结构中，我们输出的a的转置时有两对方括号，而之前只有一对方括号，这也可以体现出1行5列的矩阵和一维数组的差别。

若你不完全确定一个向量的维度（$dimension$），你可以将其扔进一个断言语句（$assertionstatement$）assert(a.shape == (5,1))。

【总结】 若想要简化代码，则不要使用一维数组。总是使用 n×1 维矩阵（基本上是列向量）或 1×n 维矩阵，这样可以减少很多assert语句来节省判断矩阵和维数的时间。另外，为了确保你的矩阵或向量所需要的维数时，不要羞于reshape操作。

附上课后作业的链接：@https://blog.csdn.net/u013733326/article/details/79827273
第一、二章其他知识点参考笔记：吴恩达深度学习笔记