戴维南定理（一）

戴维南定理，又称戴维宁定理，它表示：任何一个有源二端线性网络，都可以用一个理想电压源和电阻串联的组合来等效代替。

诺顿定理：任何一个有源二端线性网络，都可以用一个理想电流源和电阻并联的组合来等效代替。

戴维南定理（又译为戴维宁定理）又称等效电压源定律，其内容是：一个含有独立电压源、独立电流源及电阻的线性网络的两端，就其外部型态而言，在电性上可以用一个独立电压源V和一个松弛二端网络的串联电阻组合来等效。在单频交流系统中，此定理不仅只适用于电阻，也适用于广义的阻抗。uoc 称为开路电压。Ro称为戴维南等效电阻。在电子电路中，当单口网络视为电源时，常称此电阻为输出电阻，常用Ro表示；当单口网络视为负载时，则称之为输入电阻，并常用Ri表示。电压源uoc和电阻Ro的串联单口网络，常称为戴维南等效电路。

二端网络

在学习戴维南定理之前，先来学习一个新的概念：二端网络。

图1-1 二端网络

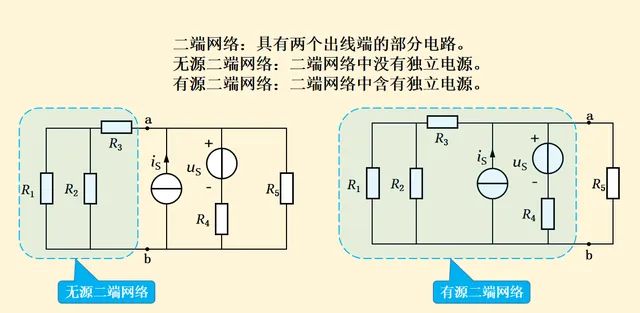
二端网络就是具有两个出线端的部分电路，如图1-1所示的闭合面部分，a、b为两个出线端，即a-b端口，包括无源二端网络和有源二端网络。在曹老师的课程内容中，无源二端网络是二端网络中没有电源；有源二端网络是二端网络中含有电源。

补充说明：所谓电源其实指的是独立电源，独立电源是区别于受控电源。

理想情况下，独立电源两端的电压或电流是恒定的，如干电池、发电机等；而受控源两端的电压或电流是可变的，如模拟电路中的放大电路等。

另外，二端网络也叫一端口网络，所以无源二端网络也可以称为无源一端口网络，有源二端网络也可以称为含源一端口网络。

如下图1-2所示，一端口网络只有一个端口a-b，以供与外电路连接，而二端口网络有两个端口1-1’和a-b，四个接线端。

图15-2 端口网络

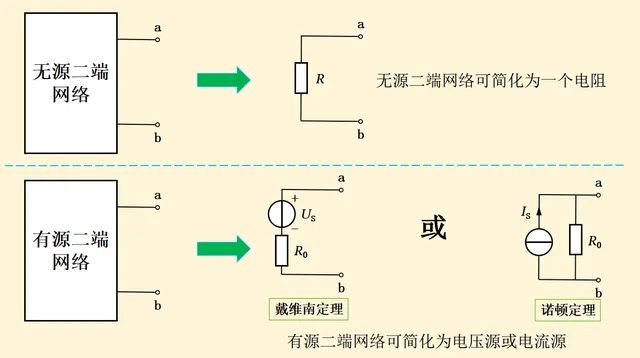
对于无源二端网络（仅含线性电阻），根据线性电路的性质，我们可以通过利用电阻的串并联和星形-三角形连接的等效变换简化为一个电阻，即等效电阻。

基于戴维南定理和诺顿定理在电路分析中的解决方法大同小异。

图1-3 戴维南定理和诺顿定理

图15-3示出无源二端网络和有源二端网络的化简。我们可以看到，有源二端网络和无源二端网络所化简的电路，区别也是在于是否含有电源。

根据戴维南定理可以把有源二端网络化简为带内阻的电压源，诺顿定理可以把有源二端网络化简为带内阻的电流源。我们以一个例子来推理一下有源二端网络的等效替换过程，如下图15-4所示。

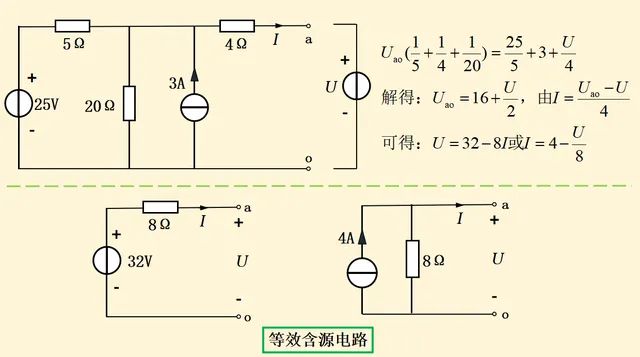
图1-4 有源二端网络的等效替换过程

从等效的简化电路与原来的一端口必须具有相同的端口外特性出发，图15-4中原电路

是一个含源一端口，为了求其端口的伏安特性，可以设想在端口a-o处加一个电压源U，然后求解端口电流I，从而得出U和I的函数关系。

利用节点电压法列出节点电压方程求解，如图1-4所示，化简出来的结果用含源支路表示，左边的称为戴维南等效电路，右边的称为诺顿等效电路。

这里的“等效”是指对端口外等效，其内部不等效。例如图1-4中的原电路和戴维南等效电路对比，原电路内部的部分电阻中是有电流流过的，即内部电路有功率的消耗，而戴维南等效电路显然不存在功率的消耗。

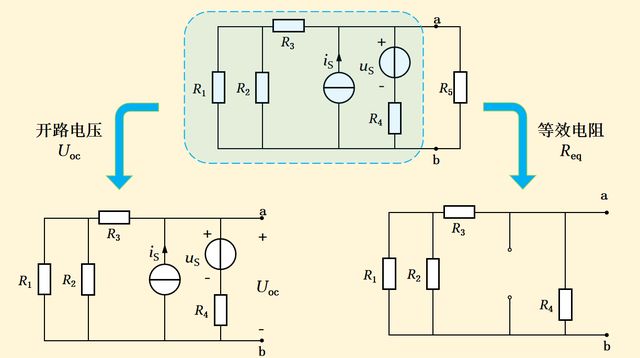
根据戴维南定理，其等效电路中，电压源的电压等于有源二端网络的开端电压，即出线端开路时网络在端口上的电压；

等效电压源的内阻等于有源二端网络相应无源二端网络的输入电阻，即把网络内部全部电源置零后的输入电阻。图1-5示出了其变换电路的处理。

图1-5 变换电路

 

在图15-5中，我们可以看到，在计算开路电压时，把端口外电路部分去掉，即端口作开路处理；在计算等效电阻（内阻）时，把所有独立电源置零，即把电压源作短路处理，把电流源作开路处理。

在使用戴维南定理进行电路分析计算时，有3个步骤：

（1）求出有源二端网络的开路电压uoc；

（2）将有源二端网络的所有独立电源置零，即将电压源短路，电流源开路，求出无源二端网络的等效电阻Req。

（3）画出戴维南等效电路图。

接下来我们以一个例题来理解戴维南定理的应用，如下图1-6所示的例题。

图1-6 例题1

 

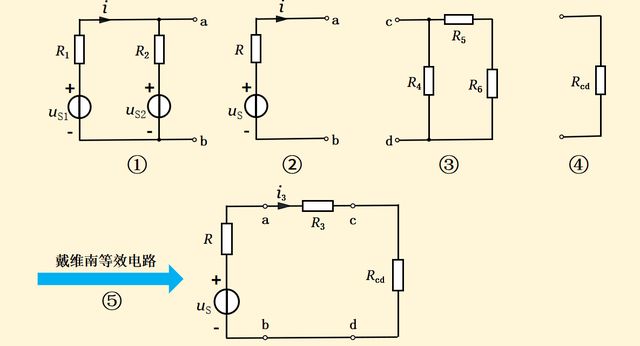
我们将电阻R3的左右两部分的电路都看为二端口网络从而加以简化。左侧是一个含源一端口，求开路电压及等效电阻较为方便，它的等效电路图如下图1-7的②所示；

再求右侧的无源一端口的等效电阻，如图1-7的④所示；

最后画出简化电路图，进而求出通过R3的电流i3。

图1-7 处理过程

图1-7中的①图简化为②图、③图简化为④图的计算过程与结果如图1-8所示；最后计算出通过R3的电流i3。

图1-8 计算过程