马尔可夫链(Markov Chain)是什么?通俗易懂
马尔可夫链(Markov Chain)
马尔可夫链经常出现在机器学习的概念中,因为生活中很多情况都可以用马尔可夫链建模,我们先给出数学化的定义,然后再举个生活化的例子与数学公式相对应,就可以理解马尔可夫链了。
ps:可以先看生活化的例子,再去看数学公式,更容易理解
数学定义
马尔可夫链是一组离散随机变量的集合。具体地,给定随机变量集合 X = { X n : n > 0 } X=\{X_n: n>0\} X={Xn:n>0},若随机变量的取值都在可数集内 X = s i , s i ∈ s X=s_{i}, s_{i} \in s X=si,si∈s:
p ( X t + 1 ∣ X t , … , X 1 ) = p ( X t + 1 ∣ X t ) p\left(X_{t+1} \mid X_{t}, \ldots, X_{1}\right)=p\left(X_{t+1} \mid X_{t}\right) p(Xt+1∣Xt,…,X1)=p(Xt+1∣Xt)
则 X X X 被称为马尔可夫链,可数集 s ∈ Z s \in Z s∈Z被称为状态空间(state space),马尔可夫链在状态空间内的取值称为状态。
上式在定义马尔可夫链的同时定义了马尔可夫性质,该性质也被称为“无记忆性(memorylessness)”,即t+1步的随机变量在给定第t步随机变量后与其余的随机变量条件独立(conditionally independent)。
生活化例子1
马尔科夫链的一个常见例子是简化的股票涨跌模型:
若一天中某股票上涨,则明天该股票有概率p开始下跌,1-p继续上涨;若一天中该股票下跌,则明天该股票有概率q开始上涨,1-q继续下跌。则该股票的涨跌情况是一个马尔可夫链,且数学定义中各个概念在该例子中有如下对应:
马尔可夫链就是一个随机过程,该例子中股票某时间段内涨跌情况,涨跌过程,即可以定义为马尔可夫链。
- 随机变量X:第t天该股票的状态;状态空间s:“上涨”和“下跌”;指数集:天数。
- 条件概率关系:按定义,即便已知该股票的所有历史状态,其在某天的涨跌也仅与前一天的状态有关。
- 无记忆性:该股票当天的表现仅与前一天有关,与其他历史状态无关(定义条件概率关系的同时定义了无记忆性)。
生活化例子2
先说说我们村智商为0的王二狗,人傻不拉几的,见人就傻笑,每天中午12点的标配,仨状态:吃,玩,睡。这就是传说中的状态分布,也就是说公式里的 s i s_i si取值只有三个吃、玩、睡。

你想知道他n天后中午12点的状态么(也就是公式里的随机变量X)?
是在吃,还是在玩,还是在睡?这些状态发生的概率分别都是多少? (知道你不想,就假装想知道吧学习真的好累)
先看个假设,他每个状态的转移都是有概率的,比如今天玩,明天睡的概率是几,今天玩,明天也玩的概率是几几,看图更清楚一点。
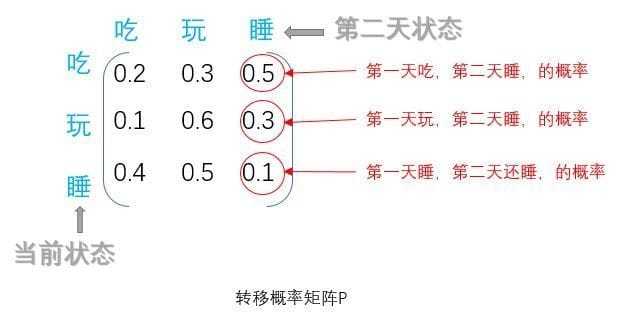
这个矩阵就是转移概率矩阵P,并且它是保持不变的,就是说第一天到第二天的转移概率矩阵跟第二天到第三天的转移概率矩阵是一样的。
有了这个矩阵,再假设我们知道他第一天的状态分布,就可以计算出第N天的状态分布了。

S1 是4月1号中午12点的的状态分布矩阵 [0.6, 0.2, 0.2],里面的数字分别代表吃的概率,玩的概率,睡的概率。
那么
4月2号的状态分布矩阵 S2 = S1 * P (俩矩阵相乘)。
4月3号的状态分布矩阵 S3 = S2 * P (看见没,跟S1无关,只跟S2有关)。
4月4号的状态分布矩阵 S4 = S3 * P (看见没,跟S1,S2无关,只跟S3有关)。
…
4月n号的状态分布矩阵 Sn = Sn-1 * P (看见没,只跟它前面一个状态Sn-1有关)。
就把下面这幅图想象成是一个马尔可夫链吧。实际上就是一个随机变量随时间按照马尔可夫性质进行变化的过程。
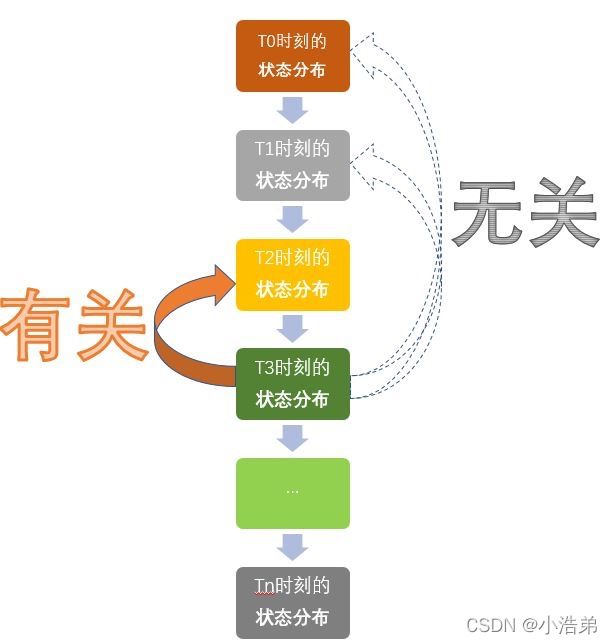
附:S2 的计算过程 (没兴趣的同学自行略过),概率论的加法原理

参考链接:
马尔可夫链是什么鬼?-知乎
马尔可夫链 -百度百科