马尔可夫链(Markov chain)的性质
本文内容主要参考:李航老师的《统计学习方法》
以下介绍离散状态马尔可夫链的性质。可以自然推广到连续状态马尔可夫链。
一、不可约

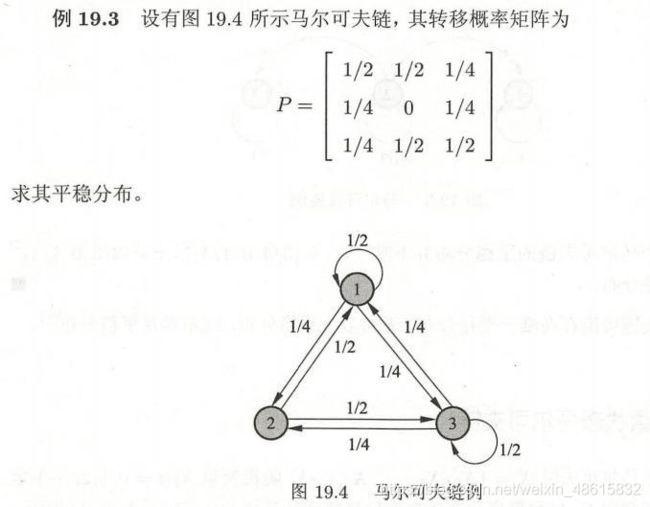
直观上,一个不可约的马尔可夫链,从任意状态出发,当经过充分长时间后,可以到达任意状态。马尔可夫链(Markov chain)的基本认识中的例19.3中的马尔可夫链是不可约的,而下面的例19.5的马尔可夫链是可约的。


求平稳分布:
from sympy import *
x1, x2, x3 = symbols('x1, x2, x3')
I = x1 + x2 + x3 -1
P = Matrix([[0, 1/2, 0], [1, 0, 0], [0, 1/2, 1]])
S = Matrix([[x1], [x2], [x3]])
print(solve([P*S-S, I],[x1,x2,x3]))
结果:
{x3: 1.00000000000000, x2: 0.0, x1: 0.0}
求之后的状态:
#离散状态马尔可夫链
from numpy import *
P = array([[0, 1/2, 0], [1, 0, 0], [0, 1/2, 1]]) #转移矩阵
Init_State = array([[1], [0], [0]]) #初始状态分布
n = 25
for i in range(1,n+1):
S = dot(P, Init_State) #dot()是点乘函数
print(f'第{i}个状态:{S.T}') #T的作用是将矩阵转置,将n*1变为1*n
Init_State = S
结果:
第1个状态:[[0. 1. 0.]]
第2个状态:[[0.5 0. 0.5]]
第3个状态:[[0. 0.5 0.5]]
第4个状态:[[0.25 0. 0.75]]
第5个状态:[[0. 0.25 0.75]]
第6个状态:[[0.125 0. 0.875]]
第7个状态:[[0. 0.125 0.875]]
第8个状态:[[0.0625 0. 0.9375]]
第9个状态:[[0. 0.0625 0.9375]]
第10个状态:[[0.03125 0. 0.96875]]
第11个状态:[[0. 0.03125 0.96875]]
第12个状态:[[0.015625 0. 0.984375]]
第13个状态:[[0. 0.015625 0.984375]]
第14个状态:[[0.0078125 0. 0.9921875]]
第15个状态:[[0. 0.0078125 0.9921875]]
第16个状态:[[0.00390625 0. 0.99609375]]
第17个状态:[[0. 0.00390625 0.99609375]]
第18个状态:[[0.00195312 0. 0.99804688]]
第19个状态:[[0. 0.00195312 0.99804688]]
第20个状态:[[9.76562500e-04 0.00000000e+00 9.99023438e-01]]
第21个状态:[[0.00000000e+00 9.76562500e-04 9.99023438e-01]]
第22个状态:[[4.88281250e-04 0.00000000e+00 9.99511719e-01]]
第23个状态:[[0.00000000e+00 4.88281250e-04 9.99511719e-01]]
第24个状态:[[2.44140625e-04 0.00000000e+00 9.99755859e-01]]
第25个状态:[[0.00000000e+00 2.44140625e-04 9.99755859e-01]]
如果采用平稳分布作为初始分布:
#离散状态马尔可夫链
from numpy import *
P = array([[0, 1/2, 0], [1, 0, 0], [0, 1/2, 1]]) #转移矩阵
Init_State = array([[0], [0], [1]]) #初始状态分布
n = 5
for i in range(1,n+1):
S = dot(P, Init_State) #dot()是点乘函数
print(f'第{i}个状态:{S.T}') #T的作用是将矩阵转置,将n*1变为1*n
Init_State = S
结果:
第1个状态:[[0. 0. 1.]]
第2个状态:[[0. 0. 1.]]
第3个状态:[[0. 0. 1.]]
第4个状态:[[0. 0. 1.]]
第5个状态:[[0. 0. 1.]]
二、非周期(周期性)
![]()

直观上,一个非周期性的马尔可夫链,不存在一个状态,从这一个状态出发,再返回到这个状态时所经历的时间长呈一定的周期性。例19.3中的马尔可夫链是非周期的,下面的例19.6中的马尔可夫链是周期的。
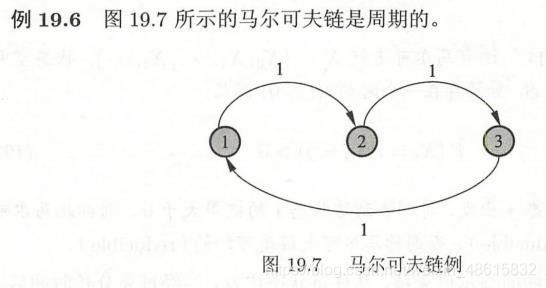

平稳分布:
from sympy import *
x1, x2, x3 = symbols('x1, x2, x3')
I = x1 + x2 + x3 -1
P = Matrix([[0, 0, 1], [1, 0, 0], [0, 1, 0]])
S = Matrix([[x1], [x2], [x3]])
print(solve([P*S-S, I],[x1,x2,x3]))
结果:
{x3: 1/3, x2: 1/3, x1: 1/3}
求之后的状态进行验证:
#离散状态马尔可夫链
from numpy import *
P = array([[0, 0, 1], [1, 0, 0], [0, 1, 0]]) #转移矩阵
Init_State = array([[1], [0], [0]]) #初始状态分布
n = 10
for i in range(1,n+1):
S = dot(P, Init_State) #dot()是点乘函数
print(f'第{i}个状态:{S.T}') #T的作用是将矩阵转置,将n*1变为1*n
Init_State = S
结果:
第1个状态:[[0 1 0]]
第2个状态:[[0 0 1]]
第3个状态:[[1 0 0]]
第4个状态:[[0 1 0]]
第5个状态:[[0 0 1]]
第6个状态:[[1 0 0]]
第7个状态:[[0 1 0]]
第8个状态:[[0 0 1]]
第9个状态:[[1 0 0]]
第10个状态:[[0 1 0]]
定理19.2: 不可约且非周期的有限状态马尔可夫链,有唯一平稳分布存在。
三、正常返

直观上,一个正常返的马尔可夫链,其中任意一个状态,从其他任意一个状态出发,当时间趋于无穷时,首次转移到这个状态的概率不为0。下面的例19.7中的马尔可夫链根据不同条件是正常返的或不是正常返的。


定理19.3:不可约、非周期且正常返的马尔可夫链,有唯一平稳分布存在。
四、遍历定理
下面叙述马尔可夫链的遍历定理。


遍历定理的直观解释:满足相应条件的马尔可夫链,当时间趋于无穷时,马尔可夫链的状态分布趋近于平稳分布,随机变量的函数的样本均值以概率1收敛于该函数的数学期望。样本均值可以认为是时间均值,而数学期望是空间均值。遍历定理的三个条件:不可约、非周期、正常返,保证了当时间趋于无穷时到达任意一个状态的概率不为0。

五、可逆马尔可夫链

直观上,如果有可逆的马尔可夫链,那么以该马尔可夫链的平稳分布作为初始分布,进行随机状态转移,无论是面向未来还是面向过去,任何一个时刻的状态分布都是该平稳分布。例19.3中的马尔可夫链是可逆的,下面的例19.8中的马尔可夫链是不可逆的。
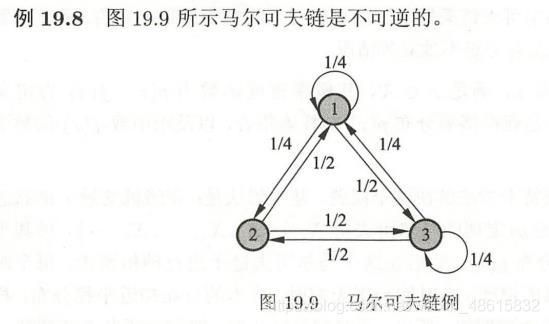

求平稳分布:
from sympy import *
x1, x2, x3 = symbols('x1, x2, x3')
I = x1 + x2 + x3 -1
P = Matrix([[1/4, 1/2, 1/4], [1/4, 0, 1/2], [1/2, 1/2, 1/4]])
S = Matrix([[x1], [x2], [x3]])
print(solve([P*S-S, I],[x1,x2,x3]))
结果:
{x3: 0.400000000000000, x2: 0.280000000000000, x1: 0.320000000000000}
求状态:
#离散状态马尔可夫链
from numpy import *
P = array([[0, 0, 1], [1, 0, 0], [0, 1, 0]]) #转移矩阵
Init_State = array([[0.32], [0.28], [0.4]]) #初始状态分布
n = 10
for i in range(1,n+1):
S = dot(P, Init_State) #dot()是点乘函数
print(f'第{i}个状态:{S.T}') #T的作用是将矩阵转置,将n*1变为1*n
Init_State = S
结果:
第1个状态:[[0.4 0.32 0.28]]
第2个状态:[[0.28 0.4 0.32]]
第3个状态:[[0.32 0.28 0.4 ]]
第4个状态:[[0.4 0.32 0.28]]
第5个状态:[[0.28 0.4 0.32]]
第6个状态:[[0.32 0.28 0.4 ]]
第7个状态:[[0.4 0.32 0.28]]
第8个状态:[[0.28 0.4 0.32]]
第9个状态:[[0.32 0.28 0.4 ]]
第10个状态:[[0.4 0.32 0.28]]
此马尔可夫链是不可逆的,即不满足细致平稳方程。
求平稳分布:
from sympy import *
x1, x2, x3 = symbols('x1, x2, x3')
I = x1 + x2 + x3 -1
P = Matrix([[1/2, 1/2, 1/4], [1/4, 0, 1/4], [1/4, 1/2, 1/2]])
S = Matrix([[x1], [x2], [x3]])
print(solve([P*S-S, I],[x1,x2,x3]))
结果:
{x3: 0.400000000000000, x2: 0.200000000000000, x1: 0.400000000000000}
求之后的状态分布:
#离散状态马尔可夫链
from numpy import *
P = array([[1/2, 1/2, 1/4], [1/4, 0, 1/4], [1/4, 1/2, 1/2]]) #转移矩阵
Init_State = array([[0.4], [0.2], [0.4]]) #初始状态分布
n = 10
for i in range(1,n+1):
S = dot(P, Init_State) #dot()是点乘函数
print(f'第{i}个状态:{S.T}') #T的作用是将矩阵转置,将n*1变为1*n
Init_State = S
结果:
第1个状态:[[0.4 0.2 0.4]]
第2个状态:[[0.4 0.2 0.4]]
第3个状态:[[0.4 0.2 0.4]]
第4个状态:[[0.4 0.2 0.4]]
第5个状态:[[0.4 0.2 0.4]]
第6个状态:[[0.4 0.2 0.4]]
第7个状态:[[0.4 0.2 0.4]]
第8个状态:[[0.4 0.2 0.4]]
第9个状态:[[0.4 0.2 0.4]]
第10个状态:[[0.4 0.2 0.4]]
