【NeurIPS 2020】ᐕ)⁾⁾5篇GNN相关论文

推荐5篇 NeurIPS 2020 接收的5篇 GNN 相关论文.分别为：
1. 随机游走图神经网络
2. 图神经网络中基于路径积分的卷积和池化算法
3. 大型随机图上的图卷积网络的收敛性和稳定性
4. Erdős Goes Neurical：一种图上组合优化的无监督学习框架
5. 用有限状态自动机层学习图结构
6. GNN 学习资料

1. Random Walk Graph Neural Networks

https://www.lix.polytechnique.fr/~nikolentzos/files/rw_gnns_neurips20

大多数 GNN 属于消息传递神经网络（MPNNs）。这些模型使用迭代邻域聚合方案来更新顶点表示。然后，为了计算图的向量表示，它们使用一些置换不变函数来聚合顶点的表示。因此，MPNNs 将图视为集合，似乎忽略了从图拓扑中产生的特征。
此文提出了一种更直观、更透明的图结构数据结构，称为随机游走图神经网络（RWNN）。

• 该模型的第一层由许多可训练的“隐藏图”组成，使用随机游走核将这些图与输入图进行比较，以产生图表示。

• 然后，这些表示被传递到一个全连接的神经网络，该神经网络产生输出。

所采用的随机游走核是可微的，因此，所提出的模型是端到端可训练的。
在合成数据集上演示了该模型的透明性。此外，在图分类数据集上对该模型进行了实证评估，结果表明该模型取得了较好的性能。

模型图

实验结果

2. Path Integral Based Convolution and Pooling for Graph Neural Networks

https://arxiv.org/abs/2006.16811

图神经网络(GNNs)将传统神经网络的功能扩展到图结构数据。与CNN类似，图的卷积和池化的优化设计是成功的关键。

借鉴物理学的思想，提出了一种基于路径积分的图神经网络(PAN)，用于图的分类和回归任务。

• 文章考虑一种卷积运算，它涉及连接消息发送者和接收者的每条路径，具有取决于路径长度的可学习权重，该路径长度对应于最大熵随机游走。

• 它将图的拉普拉斯矩阵推广到一个新的转移矩阵，称之为最大熵转移(MET)矩阵，它是由路径积分形式导出的。重要的是，MET矩阵的对角线与子图中心性直接相关，从而提供了自然和自适应的池化机制。

• PAN提供了一个多功能的框架，可以很好的适用于具有不同大小和结构的不同图数据，也可以将大多数现有的GNN体系结构视为PAN的特例。

实验结果表明，PAN在各种图形分类/回归任务上都达到了最先进的性能，其中包括作者提出的一个新的统计力学基准数据集，以促进GNN在物理科学中的应用。

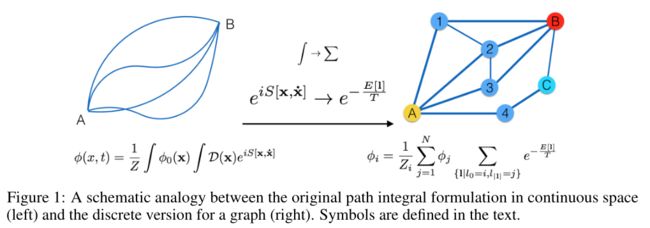连续空间的原始路径积分公式(左)和图的离散版本(右)之间的示意图类比

实验结果

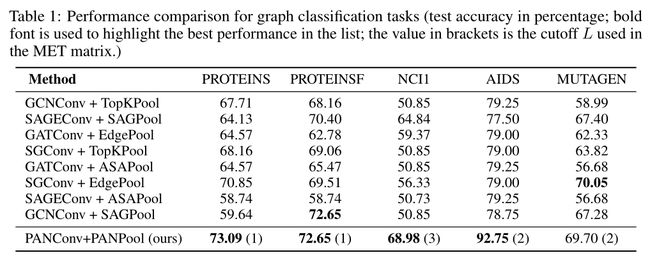图分类任务的性能比较

3. Convergence and Stability of Graph Convolutional Networks on Large Random Graphs

https://arxiv.org/abs/2006.01868

通过分析图卷积网络(GCNS)在随机图标准模型上的行为，研究GCNS的性质，其中节点用随机隐变量表示，边根据相似核来绘制。这使得我们可以通过考虑更自然的几何层面来克服处理离散概念的困难，例如非常大的图上的同构。

• 文章首先研究了GCNS随着节点数的增加而收敛到连续节点的问题。得到的结果是完全非渐近的，并且对于平均度随节点数对数增长的相对稀疏图是有效的。

• 然后，作者分析了GCNS对随机图模型的小变形的稳定性。与以前关于离散环境下稳定性的研究不同，此文的连续设置允许我们提供更直观的基于形变的度量来理解稳定性，这些度量被证明对于解释欧几里德域上卷积表示的成功是有用的。

4. Erdős Goes Neural: an Unsupervised Learning Framework for Combinatorial Optimization on Graphs

https://arxiv.org/abs/2006.10643

组合优化(CO)问题对于神经网络来说是出了名的挑战，特别是在没有标记实例的情况下。

此文针对图上的CO问题提出了一种无监督学习框架。受Erdős概率方法的启发，使用神经网络来参数化集合上的概率分布。

重要的是，作者证明了当网络针对适当选择的损失进行优化时，学习的分布以受控的概率包含符合组合问题约束的低成本积分解。然后对存在的概率证明进行随机化，以解码所需的解。

作者证明了该方法在获得最大团问题的有效解和执行局部图聚类方面的有效性。提出的方法在真实数据集和合成硬实例上都取得了有竞争力的结果。

5. Learning Graph Structure With A Finite-State Automaton Layer

https://arxiv.org/abs/2007.04929

基于图的神经网络模型在许多领域产生了强大的结果，部分原因是图提供了以图中节点之间的关系结构(边)的形式编码领域知识的灵活性。实际上，边既用于表示内在结构(例如，程序的抽象语法树)，也用于表示有助于下游任务推理的更抽象的关系(例如，相关程序分析的结果)。
这项工作研究了从内在图结构中学习导出抽象关系的问题。

• 基于它们在程序分析中的强大功能，考虑了由有限状态自动机所接受的基图上的路径定义的关系。

• 展示了如何通过将问题放松为在基于图的 POMDP 上学习有限状态自动机策略，然后使用隐式微分来训练这些策略，从而端到端地学习这些关系。

• 结果是一个可微图有限状态自动机(GFSA)层，它向基图添加了一种新的边类型(表示为加权邻接矩阵)。文章演示了这一层可以在网格世界图形中找到捷径，并在Python程序上重现简单的静态分析。

此外，作者将GFSA层与在变量误用程序理解任务中端到端训练的更大的基于图形的模型相结合，发现使用GFSA层比使用手工设计的语义边或其他基线方法添加学习的边类型具有更好的性能。

GNN 学习资料推荐

1. GNN 相关论文集

https://github.com/Jhy1993/Awesome-GNN-Recommendation

2. GNN 视频学习课程

https://www.epubit.com/courseDetails?id=PCC72369cd0eb9e7

图机器学习（时下炙手可热新技术/8章3大模型应用）。此课程分为入门、中级和应用3个部分，深入浅出，来讲解当今最炙手可热的图机器学习。