数学表达式的处理
概述
在OJ上 会遇到一些这样的题目:
小明同学写数学四则运算,有把括号写多、写少、写错的情况,比如(A+B)*(C-D ,请你输入一个表达式,判断此表达式的括号是否正确(不考虑运算的结果正确性)。
每次我看到 "括号"、算数表达式,我的第一反应就是 栈、树遍历,逆波兰表达式这些概念。
此文,我们就来探讨一下这类算法的使用。
一、栈
此处我就不想太过深入的讲解其原理了,都是数据结构基础,知道它是FILO的就行了。
栈本质上来说,是一个线性表,存储结构可以是顺序的(连续内存划分),也可以是链表
栈是允许在同一端进行插入和删除操作的特殊线性表。
允许进行插入和删除操作的一端称为栈顶(top),另一端为栈底(bottom);
栈底固定,而栈顶浮动;
栈中元素个数为零时称为空栈。
插入一般称为进栈(PUSH),删除则称为退栈(POP)。栈也称为先进后出表。
1、我们在什么情况下会用到栈?
在JVM中,我们常听说 虚拟机栈的概念,虚拟机栈是存在于运行时数据区的一个逻辑单元,它由一个个栈帧(Stack frame)构成,在当前线程中,每进行一次函数调用,就会形成一个栈帧。当进行一次方法调用,虚拟机会压入一个栈帧、方法结束的时候,会弹出该栈帧。
比如 方法 m1,m2, m3
m3 调用m2 ,m2 调用m1,我们进行一次测试:
package com.huawei.oj;
/**
* @Title:
* @Description: Method called ,JVM stack Frame struct
* @author: Alex
* @Version:
* @date 2023-01-22-8:20
*/
public class StackDemo {
public static void main(String[] args) {
m3();
}
public static int m1(){
System.out.println("m1 开始");
int i=10;
System.out.println("m1 结束");
return i;
}
public static int m2(){
System.out.println("m2开始");
int i = m1();
System.out.println("m2结束");
return i;
}
public static int m3(){
System.out.println("m3开始");
int i = m2();
System.out.println("m3结束");
return i;
}
}
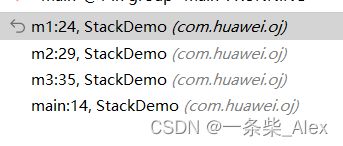
Debug我们看到,函数调用(压栈)顺序 Main---->m3 ------>m2---->m1
输出结果,我们也能看到压栈和弹栈的顺序,也是满足 FILO的:
2、为什么说到栈?
前面说的这道题,最典型的解题思路,就是栈。
思路:
判断表达式的括号是否正确:
1、括号的数量是对称相等的(这一步判断并不是必须的,因为2,和3 其实可以完全涵盖1)
2、每个左括号,后面必然有一个右括号等待与之匹配
3、不能以右括号 )开头,或者以左括号 )结尾
这里对第二点进行补充:
左括号之后并不一定就是右括号,因为会有括号嵌套的现象,比如 ((A+B)*C) -D)
满足上述几个条件后,我们用栈去解答如何设计算法:
设计算法:
1、遍历表达式字符串
2、遇见左括号就压栈,
3、遇见右括号,先判断栈是否为空,不为空就弹栈,为空,直接返回“表达式书写错误”
4、遍历完成,判断栈是否为空,为空,返回表示表达式正确,不为空,说明栈内还有左括号,返回表达式书写错误
具有代码实现:
package com.huawei.oj;
import java.util.Scanner;
import java.util.Stack;
/**
* @Title:
* @Description: TODO
* @author: Alex
* @Version:
* @date 2023-01-22-8:48
*/
public class Express {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String str = scanner.nextLine();
Stack stack = new Stack<>();
for(int i=0;i 3、关于二叉树的遍历和中缀、前缀 后缀表达式
首先我们要知道,正常人类阅读,书写表达式的时候,用的是中缀表达式,我们可以改写成表达式树的中序遍历,根据此表达式树,我们进行前序遍历、后续遍历,就可以得到这个表达式的前缀表达式和后缀表达式。
前序遍历: 又叫先根遍历,
遍历顺序:根,左,右: A BDE CFG
中序遍历:左根右 DBE A FCG
后续遍历: 左右根 DEB FGC A
如图所示:
那么 二叉树的这三种遍历,跟提到的三种表达式有什么关系?
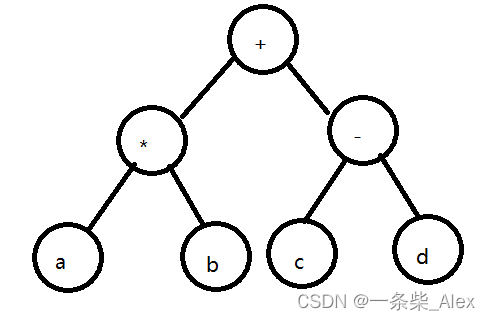
首先,我们常见的表达式,是中序表达式,比如 a*b+c-d
那么如果我们用二叉树的形式来表示它,该如何表示?
我们发现,中序遍历正好可以对应,将操作符放入非叶子节点内(即节点 A B C)
能总结出规律,就是郝兆头! 说明,我们可以用代码去实现它:
先不写代码,我们看看后缀表达式(通过对此表达式树的后续遍历得到):
后缀表达式我们知道,它还有一个名字叫:逆波兰表达式,
对于a*b+c-d 我们可以改写成 ab *cd-+
同样的,我们通过前序遍历,就可以得到它的前缀表达式:
+*ab-cd
我们再随机写一个复杂的表达式:
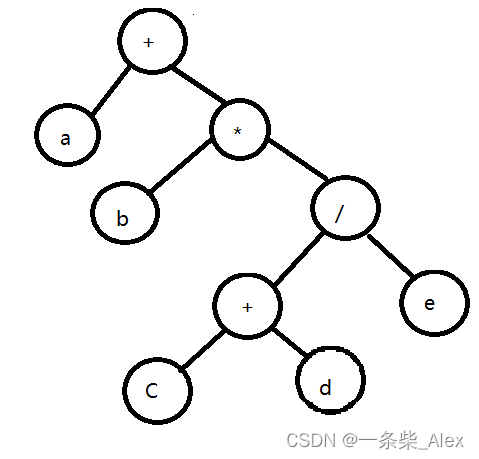
a+b*(c-(c+d)/e)
我们经历了上面的分析,现在要开始规范化,步骤化:
1)根据中序表达式,写出表达式树:
2)通过表达式树,我们写出前序遍历 和后续遍历 对应前缀和后缀表达式:
前缀表达式:+a*b/+cde
后缀表达式: abcd+e/*+
那么,我们如何通过Java代码来实现这种数据结构关系?
在当年我们用C语言学习数据结构的时候,发现关于树的遍历,书本上总是用到了栈,思考一下,为什么?
其实我们不难去理解一个问题:
树的遍历应该是递归的。
为什么?想遍历一棵树,首先应该理解,每个节点都有自己的左孩子、右孩子。
那么它的左孩子呢?是不是也有自己的左孩子和有孩子?(虽然可能为空)
右孩子的道理也是相同的。
我们知道,递归的构成: 递归出口+递归逻辑。
我们举例中序遍历说起:
递归逻辑:
在一棵最小化的模型上:
1)访问当前节点的左孩子
2)如果当前节点的左孩子为null,访问当前节点(准确的说法是,当前指针已经移动到左孩子,发现节点为null,指针回退到该节点访问)
3)访问该节点的右孩子,
4)返回操作1 (递归)
代码实现:
/**
* 节点类
*/
class Node{
int data; //节点的值
Node left; //左孩子指针
Node right; //右孩子节点
public Node(int data) {
this.data = data;
}
}三种遍历:
//中序遍历
public static void mid_Traversal(Node treeNode){
if(treeNode==null){ //如果当前节点空,直接返回
return;
}
mid_Traversal(treeNode.left);
System.out.print(treeNode.data+" ");
mid_Traversal(treeNode.right);
}
//前序遍历
public static void preorder_Traversal(Node treeNode){
if(treeNode==null){ //如果当前节点空,直接返回
return;
}
System.out.print(treeNode.data+" ");
preorder_Traversal(treeNode.left);
preorder_Traversal(treeNode.right);
}
//后序遍历
public static void subseoder_Traversal(Node treeNode){
if(treeNode==null){ //如果当前节点空,直接返回
return;
}
subseoder_Traversal(treeNode.left);
subseoder_Traversal(treeNode.right);
System.out.print(treeNode.data+" ");
}层序创建二叉树:
//创建二叉树(层序创建) 思路:根节点存放在 i位,left存放 2i+1 right存放 2i+2
public static Node createBinaryTree(int[] arr,int i){
if(arr==null||i>=arr.length){ //递归出口
return null;
}
Node root = new Node(arr[i]);
root.left=createBinaryTree(arr,2*i+1);
root.right=createBinaryTree(arr,2*i+2);
return root;
}
其实,二叉树的和栈的关系是非常密切的。
在对二叉树遍历的时候,我们可以用栈或队列实现,而不用递归。
package com.huawei.oj;
import javax.swing.tree.TreeNode;
import java.util.Stack;
/**
* @Title:
* @Description: TODO
* @author: Alex
* @Version:
* @date 2023-01-22-22:54
*/
public class StackTreeDemo {
public static void main(String[] args) {
//测试数据
int arr[] = new int[]{1, 2, 3, 4, 5, 6, 7};
Node binaryTree = MyTree.createBinaryTree(arr, 0);
//preoderTraversal(binaryTree);
// inoderTraversal(binaryTree);
postOrderTraversal(binaryTree);
}
/**
* 前序遍历:根左右
*
* @param root
*/
public static void preoderTraversal(Node root) {
Stack stack = new Stack<>();
Node node = root; //
while (node != null || !stack.isEmpty()) {
while (node != null) {
System.out.print(node.data + " ");
stack.push(node);
node = node.left;
}
if (!stack.isEmpty()) {
node = stack.pop();
node = node.right;
}
}
}
//中序遍历
public static void inoderTraversal(Node root) {
Stack stack = new Stack<>();
Node node = root;
while (node != null || !stack.isEmpty()) {
stack.push(node);
node = node.left;
while (node == null && !stack.isEmpty()) {
node = stack.pop();
System.out.print(node.data + " ");
node = node.right;
}
}
}
public static void postOrderTraversal(Node root) {
//后序遍历 左孩子、右孩子、顶点
Stack stack = new Stack<>();
Node treeNode = root;
//记录最后一次被访问的节点
Node preNode = null;
while (treeNode != null || !stack.isEmpty()) {
while (treeNode != null) {
//找到左侧节点并入栈
stack.push(treeNode);
treeNode = treeNode.left;
}
if (!stack.isEmpty()) {
treeNode = stack.peek();
if (treeNode.right == null || treeNode.right == preNode) {
//当前节点的右侧节点不存在或者右侧节点被访问过
treeNode = stack.pop();
System.out.print(treeNode.data + " ");
//记录最后一次被访问的节点
preNode = treeNode;
//继续回溯
treeNode = null;
} else {
//右侧节点存在则先访问右侧节点
treeNode = treeNode.right;
}
}
}
}
public void levelOrderTraversal(Node root) {
//层序遍历,使用到了队列辅助
Queue queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
Node node = queue.poll();
System.out.print(node.data + " ");
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
}