代码随想录算法训练营第16天| 104.二叉树的最大深度 559.n叉树的最大深度 111.二叉树的最小深度 222.完全二叉树的节点个数

代码随想录刷题系列文章目录

`
二叉树篇

---

104.二叉树的最大深度

首先，要了解什么是树的高度和深度
以及求高度深度，所对应的不同的遍历顺序

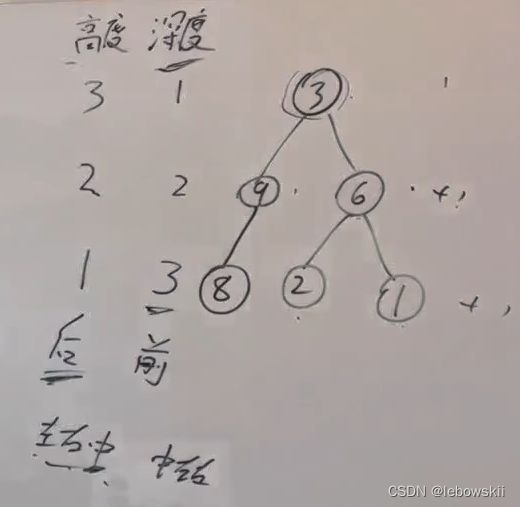
高度是，该结点到叶子结点，路径上的结点数或者距离（取决于叶子算0还是1）
深度是，该结点到根结点，路径上的结点数或者距离（取决于根算0还是1）

这两种的遍历方式是不同的，
1.算高度，从叶子往上算，需要用后序遍历，左右根；这个根其实是res计数的一个操作，是一个处理逻辑 （递归左子树， 递归右子树，处理逻辑）
2. 算深度，其实是前序的，根左右（计数 递归左子树 递归右子树）

递归法

那么为什么这道题选择用 后序的方式去做呢？ 这里还有一道逻辑转化，就是二叉树的最大深度，取决于从叶子到根的高度

所以，这道题采取后序的递归逻辑，先算左子树的高度，算右子树的高度，逻辑操作，根节点的高度取决于max(左子树，右子树）+1

后序遍历  左右根  求高度  先求左子树 再求右子树  
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root: return 0
        left = self.maxDepth(root.left)    计算左子树高度
        right = self.maxDepth(root.right)  右
        height = max(left, right)      根
        return height + 1

想清楚用什么遍历逻辑，是很重要的

bfs

用bfs也是很简单，记录一下有多少层就行了，在每一层的操作执行完后计数+1

import collections
class solution:
    def maxdepth(self, root: treenode) -> int:
        if not root:
            return 0
        depth = 0 #记录深度
        queue = collections.deque()
        queue.append(root)
        while queue:
            size = len(queue)
            depth += 1
            for i in range(size):
                node = queue.popleft()
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
        return depth

拓展 559.n叉树的最大深度

思路是一样的

class Solution:
    def maxDepth(self, root: 'Node') -> int:
        if not root: return 0
        height = 0
        for i in range(len(root.children)):
            height = max(height, self.maxDepth(root.children[i]))
        return height + 1

但是要注意，height = max(…), 这里不能加1，是最后高度只加一次1，从非root 到root这一步，而不是每一次都要加1
也可以 这么理解，算出根所有子树的最大高度，最后再+1

这个bfs模板一定要滚瓜烂熟，好多笔试题都可以用bfs去操作

def maxDepth(self, root: 'Node') -> int:
        queue = deque()
        if root:
            queue.append(root)
        layer = 0
        while queue:
            size = len(queue)
            layer += 1  #记层数
            for i in range(size):
                curr = queue.popleft()
                for j in range(len(curr.children)):
                    if curr.children[j]:
                        queue.append(curr.children[j])
        return layer

111.二叉树的最小深度

这道题和二叉树的最大深度那道题的思路是一样的，为什么用后序遍历去递归，上面已经解释过了

只不过逻辑操作取的是min

但是根据定义，深度是根节点到叶子结点的距离

递归去求根节点的最小深度的逻辑，除了 要求左子树的最小深度，右子树的最小深度，然后取最小的 +1之外， 还需要特判 左子树为空 或者 右子树为空这种情况 ； 如果有一方为空，要取另一方的最小深度

dfs 后序遍历

 def minDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        left = self.minDepth(root.left)
        right = self.minDepth(root.right)
        if root.left == None and root.right != None:
            return 1 + right
        if root.left != None and root.right ==None:
            return 1 + left
        return 1 + min(left, right)

bfs解法

class Solution:
    def minDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        queue = deque()
        queue.append(root)
        layer = 0
        while queue:
            size = len(queue)
            layer += 1
            for i in range(size):
                curr = queue.popleft()
                if not curr.left and not curr.right:
                    return layer
                if curr.left:
                    queue.append(curr.left)
                if curr.right:
                    queue.append(curr.right)

222.完全二叉树的节点个数

dfs后序遍历

def countNodes(self, root: Optional[TreeNode]) -> int:
        if not root: return 0
        lft = self.countNodes(root.left)
        right = self.countNodes(root.right)
        if not root.left and not root.right:
            return 1
        elif not root.left and root.right:
            return right + 1
        elif root.left and not root.right:
            return lft + 1
        else:
            return lft + right + 1

仔细想想完全没有必要特判空节点，因为if not root: return 0 已经有特判的条件了

if not root: return 0
        lft = self.countNodes(root.left)
        right = self.countNodes(root.right)
        return lft + right + 1

bfs方式

只需要在每个结点pop的时候，计一下数即可

import collections
class Solution:
    def countNodes(self, root: TreeNode) -> int:
        queue = collections.deque()
        if root:
            queue.append(root)
        result = 0
        while queue:
            size = len(queue)
            for i in range(size):
                node = queue.popleft()
                result += 1       #记录节点数量
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
        return result

总结

求二叉树的深度，可以转化为求高度，这样就可以用后序遍历的逻辑去处理了

这几道题的dfs写法都用了后序遍历的逻辑，即 左右根， 这里的左右是递归调用遍历左右子树，根是写处理逻辑

对于这样的题，都可以使用 后序遍历，先遍历左子树，右子树，递归累加到根