2.2 优化算法（MINI-BATCH、指数加权平均、动量梯度下降、RMSPROP、Adam优化算法、学习率衰减、局部最优）

MINI-BATCH

实际训练中，数据集过于庞大，需要拆分成一个个小的子训练集。

mini-batch梯度下降：选用子训练集进行梯度下降；

• batch梯度下降：选用整个数据集进行梯度下降；mini-batch 的大小为 m（数据集大小）；
• 随机梯度下降：选用一个样本当做一个子训练集进行梯度下降；mini-batch 的大小为 1；

术语-epoch：对整个训练集进行了一次梯度下降

两个极端例子，对比MINI-BATCH：

训练神经网络的目的：找到一组参数w、b使成本函数J最小。

若下面这个图是成本函数，它中间的点就是最小值处。

batch 梯度下降法：

• 对所有 m 个训练样本执行一次梯度下降，每一次迭代时间较长，训练过程慢；
• 相对噪声低一些，幅度也大一些；迈的步子大；
• 成本函数总是向减小的方向下降；方向正确；

随机梯度下降法：

• 对每一个训练样本执行一次梯度下降，训练速度快，但丢失了向量化带来的计算加速；
• 有很多噪声，减小学习率可以适当；（路途忐忑，步子小，可能还会迷失方向）
• 成本函数总体趋势向全局最小值靠近，但永远不会收敛，而是一直在最小值附近波动。

mini-batch梯度下降法：

因此，选择一个1 < size < m的合适的大小进行 Mini-batch 梯度下降，可以实现方向准确、步子较大，也应用了向量化带来的好处。

mini-batch梯度下降时，成本是波荡起伏的

因为某个子集中，可能错误案例比较多，导致了J偏高。但总体趋势还是J走向最低。

mini-batch 的不同大小（size）也是一个超参数

• 如果训练样本的大小比较小，如 m ⩽ 2000 时，选择 batch 梯度下降法；
• 如果训练样本的大小比较大，选择 Mini-Batch 梯度下降法。为了和计算机的信息存储方式相适应，代码在 mini-batch 大小为 2 的幂次时运行要快一些。典型的大小为 2626、2727、...、2929；
• mini-batch 的大小要符合 CPU/GPU 内存。

mini-batch 的大小也是一个重要的超变量，需要根据经验快速尝试，找到能够最有效地减少成本函数的值。

指数加权平均

直观理解：

# β看成K也行

w==温度：w1==第一天的温度,w2==第二天的温度

v==我们最终求的趋势值：v1表示第一天的值,v2表示第二天的值

从上面的算法我们可以看出，当天的趋势值 = k * 前一天的趋势值 + （1-k） * 当天的温度。

前一天的趋势值  代表 1 / （1-k）天的 近似的趋势值  （不是平均值）

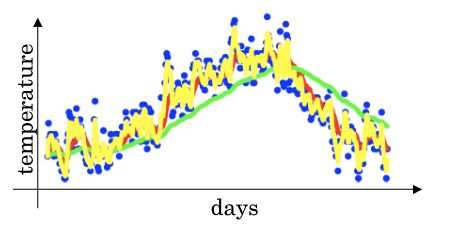
给定一个时间序列，例如伦敦一年每天的气温值，图中蓝色的点代表真实数据。

对于一个即时的气温值，取权重值 k 为 0.9，根据求得的值可以得到图中的红色曲线，（受到最近10天的影响比较大）

当取权重值 k=0.98 时，可以得到图中更为平滑的绿色曲线。（受到最近50天的影响比较大）

而当取权重值 k=0.5 时，得到图中噪点更多的黄色曲线。（受到最近2天的影响）

曲线反映了气温变化的大致趋势。

β 越大相当于求取平均利用的天数越多，曲线自然就会越平滑而且越滞后。

# 类似于K线的MA，但是k线是rolling().mean()，是简单的K线求平均。我们算的是加权MA，离现在近的数值，则权重大。

# MA中，若K线MA的参数60，则如果最近几根K线的暴涨暴跌，那么MA不会太敏感，他会计算最近60根的mean

深入理解：

9^ 1  ==  0.9
9^ 2  ==  0.81
9^ 3  ==  0.7290000000000001
9^ 4  ==  0.6561
9^ 5  ==  0.5904900000000001
9^ 6  ==  0.531441
9^ 7  ==  0.4782969000000001
9^ 8  ==  0.4304672100000001
9^ 9  ==  0.3874204890000001
9^ 10  ==  0.3486784401000001
9^ 11  ==  0.31381059609000006
9^ 12  ==  0.2824295364810001
9^ 13  ==  0.2541865828329001
9^ 14  ==  0.2287679245496101
9^ 15  ==  0.20589113209464907
9^ 16  ==  0.18530201888518416
9^ 17  ==  0.16677181699666577
9^ 18  ==  0.15009463529699918
9^ 19  ==  0.13508517176729928
9^ 20  ==  0.12157665459056935
9^ 21  ==  0.10941898913151242
9^ 22  ==  0.09847709021836118
9^ 23  ==  0.08862938119652507
9^ 24  ==  0.07976644307687256
9^ 25  ==  0.0717897987691853
9^ 26  ==  0.06461081889226677
9^ 27  ==  0.058149737003040096
9^ 28  ==  0.05233476330273609
9^ 29  ==  0.047101286972462485
9^ 30  ==  0.04239115827521624
9^ 31  ==  0.038152042447694615
9^ 32  ==  0.03433683820292515
9^ 33  ==  0.030903154382632636
9^ 34  ==  0.027812838944369374
9^ 35  ==  0.025031555049932437
9^ 36  ==  0.022528399544939195
9^ 37  ==  0.020275559590445275
9^ 38  ==  0.01824800363140075
9^ 39  ==  0.016423203268260675
9^ 40  ==  0.014780882941434608
9^ 41  ==  0.013302794647291146
9^ 42  ==  0.011972515182562033
9^ 43  ==  0.01077526366430583
9^ 44  ==  0.009697737297875247
9^ 45  ==  0.008727963568087723
9^ 46  ==  0.00785516721127895
9^ 47  ==  0.007069650490151055
9^ 48  ==  0.00636268544113595
9^ 49  ==  0.005726416897022355
9^ 50  ==  0.00515377520732012

代码实现：

# v是一个变量，只是 新的v = k * 旧的v + （1-k）wt

修正：

若w1 == 40度，则算出来 v1 == 0.8度，趋势值v1 v2 以及前面几天 均无法反映 前面一段时间的温度水平。

修正方法：

计算后：

越往后，t的值就越大，即k越来越小，那么公式中的分母就越来越靠近1,因为后面vt不需要再修正了。

其实在实际开发中,我们都不会使用修正算法。因为只是前面一点点偏离而已,不伤大雅。

动量梯度下降

比"单纯的梯度下降"好；"指数加权平均"是基础；

# 这里的动量 指的是Momentum，是物理上的动量，是用的碗里小球的例子

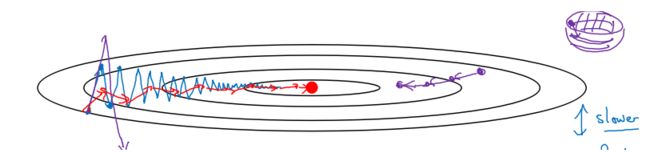
使用"一般的梯度下降"：

会得到图中的蓝色曲线,它不会径直向着最小值前进(因为他根本不知道最小值在哪里)，而且训练集中也可能有些错误的样本，所以方向也不可能百分之百很准，所以梯度下降的图像是曲折的。这种"折叠曲线的前进"比"两点之间直线最短"要效率低。
而且方向不准还导致了我们无法使用大的学习率，想快都快不了。因为如果我们使用大的学习率，那么曲线折叠的幅度会更大。下图中的紫色的线展示了用大的学习率后执行了两步，可以看出跑得更偏了，不仅不能快，反而会使学习效率下降。

使用"动量梯度下降"：

如何让曲线折叠的幅度更小一些呢?—―使用指数加权平均算法。

首先我们还是像以前一样求出梯度dw和db，然后再使用指数加权算法求出Vdw和Vdb

红线的折叠幅度很小了，幅度小了不仅能更快找到最小值，而且还可以使用大的学习率，使学习速度更快。

指数加权平均中的k变量是一个超参数。在梯度下降中我们一般把它设为0.9。

RMSPROP

原理类似，

RMSProp 有助于减少抵达最小值路径上的摆动，并允许使用一个更大的学习率 α，从而加快算法学习速度。

Adam优化算法

很多优化算法都只能适用于某几类神经网络结构，无法通吃所有情况。

直到后来动量梯度下降的出现，发现它能适用于各种网络结构。

RMSprop又出现了，它也能被广泛应用于各种网络结构中。

后来又出现了Adam优化算法(tensorflow等框架,都内置实现了Adam算法)，其实就是将动量梯度下降和RMSprop结合在一起而已。结合之后大家发现它在很多网络结构中都能表现得很出色。 

# 偏差修正指的是前面起始的数据 进行修正

超参数的选择

Adam 优化算法有很多的超参数，其中

• 学习率 α：需要尝试一系列的值，来寻找比较合适的；
• β1：常用的缺省值为 0.9；
• β2：Adam 算法的作者建议为 0.999；
• ϵ：不重要，不会影响算法表现，Adam 算法的作者建议为 10^−8；

β1、β2、ϵ 通常不需要调试。

学习率衰减

学习率r之前是固定的。其实让学习率r 随着时间 而慢慢地衰减 是有助于提升学习效率的.

为什么呢?假设我们将mini-batch的值设得很小（64），训练集越小，那么学习的方向就越容易偏离。

学习路线就有可能如下图一样，而且即使到了最小值处，也始终找不到最小值，而在它附近徘徊。

如果让学习率随着学习的次数而慢慢地变小，那么就会出现下图的情况。最开始学习率还是很大，和上图一样。

慢慢地学习率会变小学习步进会变小。从下图可以看出这样一来就可以更加靠近最小值处，找到最小值了。

刚刚开始入门时，门外汉什么都不懂,所以可以大步的粗咯学习。随着学习越来越深入，那么就越需要静下心来慢慢地进行精致的学习。

假设我们将初始的学习率a0设置为0.2，将衰减率decayRate设为1，那么套入上面的公式，

在进行了一个epoch后,a就变成了0.1，在进行了两个epoch后, a变成了0.067，第三个epoch后，a变成了0.05...

随着epoch的次数越多，a越小。

局部最优

在多维图形中，完全没有路径通向全局最优的小坑，称之为“局部最优”

在多维图形中，在小坑处，某个维度虽然如上图所示，但是其他维度，仍然有路径通向全局最优，称之为“鞍点”。

“局部最优”的概率很低，不用担心；可能鞍点很多，也不足为虑。

在“鞍点”或者“局部最优”的附近，比较“平稳”，斜率是0或者很小，要训练很长时间，才能在横向达到最小值，在竖向继续走，找寻全局最优。

• 在训练较大的神经网络、存在大量参数，并且成本函数被定义在较高的维度空间时，困在极差的局部最优中是不大可能的；
• 鞍点附近的平稳段会使得学习非常缓慢，而这也是动量梯度下降法、RMSProp 以及 Adam 优化算法能够加速学习的原因，它们能帮助尽早走出平稳段。

代码

https://gitee.com/bijingrui1997/deep_learning_notes/tree/master/2.2%20%E4%BC%98%E5%8C%96%E7%AE%97%E6%B3%95