数学建模之理想解法（TOPSIS）

本文参考的是司守奎，孙兆亮主编的数学建模算法与应用（第二版）

TOPSIS的基本思路就是从各个特征中各自抽取出最优的特征值构成一个虚拟实际不存在的解，称之为正理想解；再从各个特征中各自抽取出最劣的特征值构成另一个实际不存在的解，称之为负理想解。
最后将原有的每个特征组视作实际的解，通过比较实际解与正理想解的欧式距离和负理想解的欧式距离来评判此解的优劣，即一个实际解距离正理想解最近，距离负理想解最远，可认为此解为实际最优解，同时通过这种方法，能够得出每一个实际解的评判值，通过对这个值大小排序，即可完成对事物优劣的综合评价。
值得注意的是，TOPSIS需要构造加权规范阵，即要求得各个特征对应的权重，这个权重可以用许多方法得到，例如层次分析法、熵权法或者灰色综合评价等等。

TOPSIS求解过程如下：
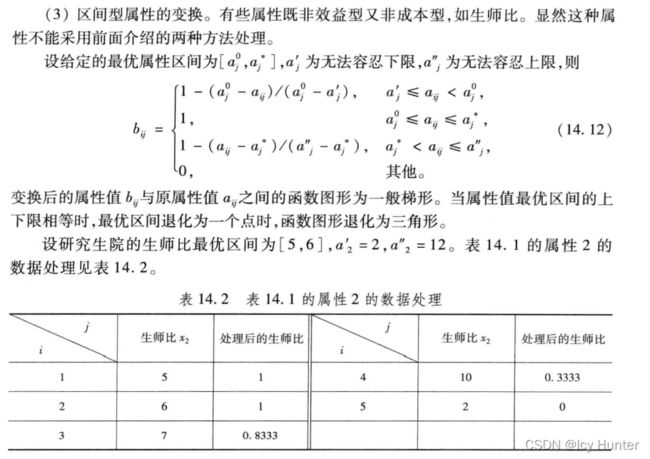
第一步，需要进行数据预处理，对指标进行相应的变换。主要是对于区间型的数据。

第二步，需要对向量规范化

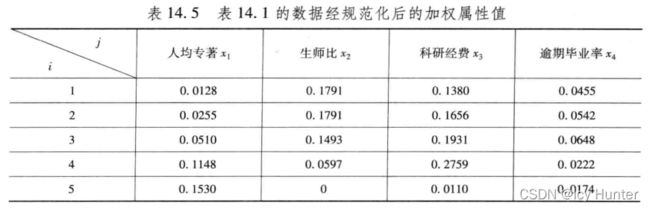
第三步，获取对应特征权重，计算出加权矩阵

第四步，计算正理想解和负理想解（由于区间型数据以通过前面转换成效益型了，这里只需要区分效益型和成本型了）

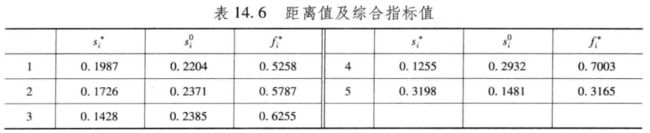
第五步，计算各个方案到正负理想解的距离

第六步，通过到正理想解的距离和到负理想解的距离来计算综合评价指数

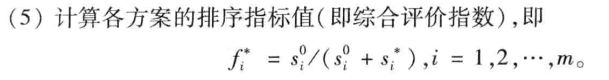
最后一步，对结果进行排序，完成评价

下面将展示一道例题：

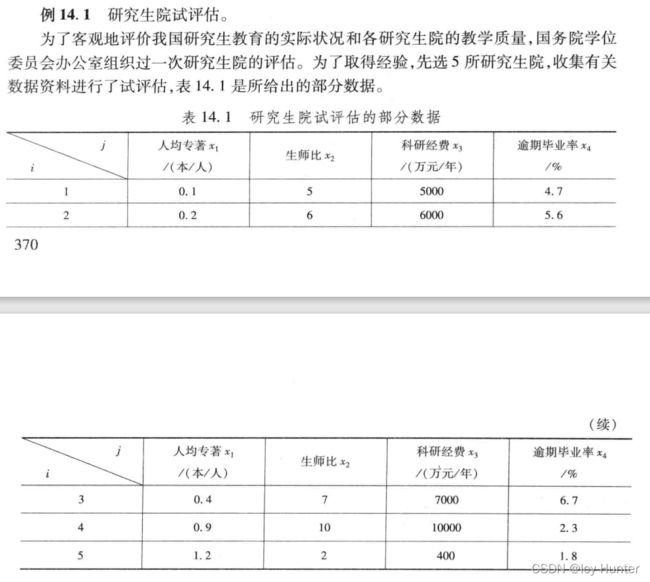
第一步，对区间型数据转化为效益型的形式

data = [0.1 5 5000 4.7
    0.2 6 6000 5.6
    0.4 7 7000 6.7
    0.9 10 10000 2.3
    1.2 2 400 1.8
     ];
 [row, col] = size(data);
 
 %定义一个函数，使得区间型指标转换为效益型指标的形式，思路就是 定义域*值域，只有当符合定义域才能获取值域，否则就为0
 analyze = @(qujian, bottom, top, x)(1 - (qujian(1) - x)./(qujian(1)-bottom)).*(x >= bottom & x < qujian(1))+...
     (x >= qujian(1) & x <= qujian(2)) * 1 +...
     (1 - (x - qujian(2))./(top - qujian(2))).*(x > qujian(2) & x <= top);
 qujian = [5,6];% 规定的最优区间
 bottom = 2;% 无法容忍的下界
 top = 12;% 无法容忍的上界
 data(:, 2) = analyze(qujian, bottom, top, data(:, 2)); % 调用函数进行指标转化

第二步，矩阵规范化

 data_norm = [];% 定义标准化的矩阵
 for j = 1:col
     data_norm(:, j) = data(:, j)/norm(data(:, j)); %对每一列进行标准化
 end

第三步，获取权重，求的加权矩阵

 w = [0.2, 0.3, 0.4, 0.1];%获取特征权重
 data_weighted = data_norm .* repmat(w, row, 1); %计算加权规范阵
 data_weighted

第四步，计算正理想解和负理想解

 Cstar = max(data_weighted);% 求正理想解
 Cstar(4) = min(data_weighted(:, 4)); % 成本型指标越小越优
 C0 = min(data_weighted);% 求负理想解
 C0(4) = max(data_weighted(:, 4)); % 成本型指标越大越劣
 
 C0,Cstar

第五步，计算各方案距离

% 计算方案到正理想解和负理想解的距离
 for i = 1:row
     Sstar(i) = norm(data_weighted(i,:) - Cstar);
     S0(i) = norm(data_weighted(i,:) - C0);
 end
 
 Sstar,S0

第六步，计算综合评分

 f = S0./(Sstar + S0)% 计算对应综合分数

最后一步，排序

 [sf, ind] = sort(f, 'descend') % 根据分数排序

matlab完整代码如下：

clc,clear
data = [0.1 5 5000 4.7
    0.2 6 6000 5.6
    0.4 7 7000 6.7
    0.9 10 10000 2.3
    1.2 2 400 1.8
     ];
 [row, col] = size(data);
 
 %定义一个函数，使得区间型指标转换为效益型指标的形式，思路就是 定义域*值域，只有当符合定义域才能获取值域，否则就为0
 analyze = @(qujian, bottom, top, x)(1 - (qujian(1) - x)./(qujian(1)-bottom)).*(x >= bottom & x < qujian(1))+...
     (x >= qujian(1) & x <= qujian(2)) * 1 +...
     (1 - (x - qujian(2))./(top - qujian(2))).*(x > qujian(2) & x <= top);
 qujian = [5,6];% 规定的最优区间
 bottom = 2;% 无法容忍的下界
 top = 12;% 无法容忍的上界
 data(:, 2) = analyze(qujian, bottom, top, data(:, 2)); % 调用函数进行指标转化
 data_norm = [];% 定义标准化的矩阵
 for j = 1:col
     data_norm(:, j) = data(:, j)/norm(data(:, j)); %对每一列进行标准化
 end
 
 w = [0.2, 0.3, 0.4, 0.1];%获取特征权重
 data_weighted = data_norm .* repmat(w, row, 1); %计算加权规范阵
 data_weighted
 
 Cstar = max(data_weighted);% 求正理想解
 Cstar(4) = min(data_weighted(:, 4)); % 成本型指标越小越优
 C0 = min(data_weighted);% 求负理想解
 C0(4) = max(data_weighted(:, 4)); % 成本型指标越大越劣
 
 C0,Cstar
 
 % 计算方案到正理想解和负理想解的距离
 for i = 1:row
     Sstar(i) = norm(data_weighted(i,:) - Cstar);
     S0(i) = norm(data_weighted(i,:) - C0);
 end
 
 Sstar,S0
 
 f = S0./(Sstar + S0)% 计算对应综合分数
 [sf, ind] = sort(f, 'descend') % 根据分数排序