综合评价与决策方法(1)---理想解法TOPSIS

概述

理想解法可以将一些方案进行优劣排序，选出适合的且综合更趋向最优的方案，并不可以求出最优解，只是在已知解中找到一个合适的优劣方案。

解释步骤

解释的只是写了一些大致的步骤，后面有例子来具体解释一些步骤。

1. 要规定一些符号，决策要素集$A$（一个1 x n的矩阵），根据决策要素而产生的解决方案集$D$(一个 m x n 的矩阵，其中m为解决方案的个数)。
2. 将解决方案中的要素规范化形成矩阵$B$。（一个 m x n 的矩阵），规范化的目的是把那些量纲不同意，或者评价方案不同意的变量同意用一个数值表示。详情请参看我的另一篇博客，请务必留意里面讲到的成本型变量和效益型变量(传送门呀！！！)
3. 将权重和对应的分量相乘对应的分量。
4. 在规范化的数据中选择出正理想解$C^{\ast }$和负理想解$C^0$，设第j个属性的正理想解为$c_j^{\ast }$，负理想集为$c_j^0$。确定准则如下：
   
5. 计算各个方案到正理想集和负理想集的距离。备选方案$d_i$到正理想解的距离：
   
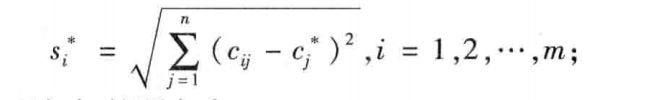
   到负理想解的距离：
6. 各个方案方案的排序指标值。
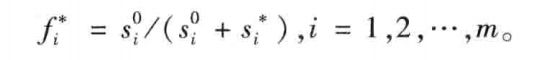
   这个非常好理解，就是到最负理想解的距离越远，这个值越大，解决方案就越优。

实例解析

我要对多个学校的状况进行评估，评估的方面包括：逾期毕业率，研究生师生比例，科研经费。列出数据如下所示：

序号	逾期毕业率	研究生师生比例	科研经费（万元/年）	人均专著
1	4.3%	5.5	5000	0.1
2	2.8%	4.5	6000	0.2
3	3.6%	10	10000	0.9
4	7.9%	7	6000	1.2
5	0.5%	8	1000	0.3

首先，规范一下符号，

• 记$A(a_{ij}{)}_{1\times n}$矩阵为评级指标矩阵，在这里就是一个1x3的矩阵
• $D(d_{ij}{)}_{m\times n}$为实际的情况数据的矩阵，在这里就是表示上面的数据，为5x3的矩阵
• $B(b_{ij}{)}_{m\times n}$为$D$规范化之后的矩阵。

开始解题：
（1）分析这些数据中，发现逾期毕业率属于成本型变量；研究生师生比例属于区间型变量；人均专著和科研经费属于效益型变量。
规范化处理，对于逾期毕业率，人均专著和科研经费我选择的处理方法是使用0-1规范化的方法，对于研究生师生比选择的是区间规范化方法，设置的最优区间为[5,7]，不可容忍区间为[3,12]。

import numpy as np
#输入数据
funds_list = np.array([5000,6000,10000,6000,1000])
booknum_list = np.array([0.1,0.2,0.9,1.2,0.3])
overdue_list = np.array([4.3,2.8,3.6,7.9,0.5])
TaSRate = np.array([5.5,4.5,10,7,8])
Combine_metrix = np.vstack((funds_list,booknum_list,overdue_list))  #数据垂直拼接,列合并

#规范化效益型数据
funds_list_mod = (funds_list - funds_list.min())/(funds_list.max()-funds_list.min())
booknum_list_mod =  (booknum_list-booknum_list.min())/(booknum_list.max()-booknum_list.min())

#规范成本型数据
overdue_list_mod = (overdue_list.max() - overdue_list)/(overdue_list.max()-overdue_list.min())

#规范化区间数据

#设置区间
interval = np.array([5,7])
notAllow = np.array([3,12])
#数据处理
TaSRate_mod = []
for t in TaSRate:
    if t<= interval[0] and t>=notAllow[0]:
        t = 1-(interval[0]-t)/(interval[0]-notAllow[0])
        TaSRate_mod.append(t)
    elif t<=interval[1] and t>=interval[0]:
        t = 1
        TaSRate_mod.append(t)
    elif t<=notAllow[1] and t>=interval[1]:
        t = 1 - (t-interval[1])/(notAllow[1]-interval[1]) 
        TaSRate_mod.append(t)
    else :
        t = 0
        TaSRate_mod.append(t)
TaSRate_mod = np.array(TaSRate_mod)
Combine_metrix = np.vstack((funds_list_mod,booknum_list_mod,overdue_list_mod,TaSRate_mod))

#结果
# [[0.44444444 0.55555556 1.         0.55555556 0.        ]
#  [0.         0.09090909 0.72727273 1.         0.18181818]
#  [0.48648649 0.68918919 0.58108108 0.         1.        ]
#  [1.         0.75       0.4        1.         0.8       ]]

(2) 求解权重矩阵，首先要设置一个权重为$$w=[0.2,0.3,0.4,0.1]$$

#权重设置
weight = np.array([0.2,0.3,0.4,0.1])
#C_metrix为最优解法矩阵
C_metrix = []
for w,col in zip(weight,Combine_metrix):
    C_metrix.append(w*col)
C_metrix = np.array(C_metrix)

#结果C_metrix
# [[0.08888889 0.11111111 0.2        0.11111111 0.        ]
#  [0.         0.02727273 0.21818182 0.3        0.05454545]
#  [0.19459459 0.27567568 0.23243243 0.         0.4       ]
#  [0.1        0.075      0.04       0.1        0.08      ]]

(3)求解正理想解和负理想解

#正理想解集
C_positive = []
#负理想解集
C_negative = []

#设置一个标识是效益型，成本型，还是区间型的矩阵,1,0,-1
classify = [1,1,0,-1]

for cas,C in zip(classify,C_metrix):
    if cas == 1:
        C_positive.append(C.max())
        C_negative.append(C.min())
    elif cas == 0:
        C_positive.append(C.min())
        C_negative.append(C.max())
    elif cas ==-1:
        C_positive.append(0.1)
        C_negative.append(C.min())

#结果
# C_position = [0.2, 0.3, 0.0, 0.1]
# C_negative = [0.0, 0.0, 0.4, 0.04]

(4)计算各个方案的正理想解与负理想解

#求解正向距离和负向距离
#求解正向距离和负向距离
S_positive = []
S_negative = []


for C_n,C_p,C_m in zip(C_negative,C_positive,C_metrix):
    S_positive.append(np.sqrt((C_m-C_p)**2))
    S_negative.append(np.sqrt((C_m-C_n)**2))
S_negative = np.array(S_negative).sum(axis=0)
S_positive = np.array(S_positive).sum(axis=0)#0是竖着加，1是横着加，2是z轴加一起


#结果
# [0.60570571 0.66229184 0.37425061 0.08888889 0.86545455]
# [0.35429429 0.29770816 0.58574939 0.87111111 0.09454545]

(5)求解排序指标值

f = []
for s_p,s_n in zip(S_positive,S_negative):
    f.append(s_n/(s_p+s_n))    
#结果
#[0.3690565565565566, 0.31011266948766947, 0.6101556101556102, 0.9074074074074074, 0.09848484848484848]

由上述结果我们找到最大的就是第四个学校。
排名如下所示：

序号	逾期毕业率	研究生师生比例	科研经费（万元/年）	人均专著	排名
1	4.3%	5.5	5000	0.1	3
2	2.8%	4.5	6000	0.2	4
3	3.6%	10	10000	0.9	2
4	7.9%	7	6000	1.2	1
5	0.5%	8	1000	0.3	5

整体代码回顾一下：

import numpy as np
#输入数据
funds_list = np.array([5000,6000,10000,6000,1000])
booknum_list = np.array([0.1,0.2,0.9,1.2,0.3])
overdue_list = np.array([4.3,2.8,3.6,7.9,0.5])
TaSRate = np.array([5.5,4.5,10,7,8])
Combine_metrix = np.vstack((funds_list,booknum_list,overdue_list))  #数据垂直拼接,列合并

#规范化效益型数据
funds_list_mod = (funds_list - funds_list.min())/(funds_list.max()-funds_list.min())
booknum_list_mod =  (booknum_list-booknum_list.min())/(booknum_list.max()-booknum_list.min())

#规范成本型数据
overdue_list_mod = (overdue_list.max() - overdue_list)/(overdue_list.max()-overdue_list.min())

#规范化区间数据

#设置区间
interval = np.array([5,7])
notAllow = np.array([3,12])
#数据处理
TaSRate_mod = []
for t in TaSRate:
    if t<= interval[0] and t>=notAllow[0]:
        t = 1-(interval[0]-t)/(interval[0]-notAllow[0])
        TaSRate_mod.append(t)
    elif t<=interval[1] and t>=interval[0]:
        t = 1
        TaSRate_mod.append(t)
    elif t<=notAllow[1] and t>=interval[1]:
        t = 1 - (t-interval[1])/(notAllow[1]-interval[1]) 
        TaSRate_mod.append(t)
    else :
        t = 0
        TaSRate_mod.append(t)
TaSRate_mod = np.array(TaSRate_mod)
Combine_metrix = np.vstack((funds_list_mod,booknum_list_mod,overdue_list_mod,TaSRate_mod))

#结果Combine_metrix
# [[0.44444444 0.55555556 1.         0.55555556 0.        ]
#  [0.         0.09090909 0.72727273 1.         0.18181818]
#  [0.48648649 0.68918919 0.58108108 0.         1.        ]
#  [1.         0.75       0.4        1.         0.8       ]]


#权重设置
weight = np.array([0.2,0.3,0.4,0.1])
#C_metrix为最优解法矩阵
C_metrix = []
for w,col in zip(weight,Combine_metrix):
    C_metrix.append(w*col)
C_metrix = np.array(C_metrix)


#结果C_metrix
# [[0.08888889 0.11111111 0.2        0.11111111 0.        ] --资金
#  [0.         0.02727273 0.21818182 0.3        0.05454545] --出版
#  [0.19459459 0.27567568 0.23243243 0.         0.4       ] --逾期毕业
#  [0.1        0.075      0.04       0.1        0.08      ]]--师生比

#正理想解集
C_positive = []
#负理想解集
C_negative = []

#设置一个标识是效益型，成本型，还是区间型的矩阵,1,0,-1
classify = [1,1,0,-1]
for cas,C in zip(classify,C_metrix):
    if cas == 1:
        C_positive.append(C.max())
        C_negative.append(C.min())
    elif cas == 0:
        C_positive.append(C.min())
        C_negative.append(C.max())
    elif cas ==-1:
        C_positive.append(0.1)
        C_negative.append(C.min())

#结果
# C_position = [0.2, 0.3, 0.0, 0.1]
# C_negative = [0.0, 0.0, 0.4, 0.04]

#求解正向距离和负向距离
S_positive = []
S_negative = []


for C_n,C_p,C_m in zip(C_negative,C_positive,C_metrix):
    S_positive.append(np.sqrt((C_m-C_p)**2))
    S_negative.append(np.sqrt((C_m-C_n)**2))
S_negative = np.array(S_negative).sum(axis=0)
S_positive = np.array(S_positive).sum(axis=0)


#结果
# [0.60570571 0.66229184 0.37425061 0.08888889 0.86545455]
# [0.35429429 0.29770816 0.58574939 0.87111111 0.09454545]


f = []
for s_p,s_n in zip(S_positive,S_negative):
    f.append(s_n/(s_p+s_n))
print(f)
#结果
#[0.3690565565565566, 0.31011266948766947, 0.6101556101556102, 0.9074074074074074, 0.09848484848484848]