动手学数据分析 TASK5 数据建模与模型评估

前言

经过前面的两章的知识点的学习，我们除了可以对数据的本身进行处理，比如数据本身的增删查补，还可以做必要的清洗工作，该过程可以统称为数据的预处理。这一章我们要做的就是使用数据，那么分析的第一步就是建模，搭建一个预测模型或者其他模型；我们从这个模型的到结果之后，则需要对该模型及进行评估以判断结果是否可靠。

一、关键词概要

数据建模：
Sklearn、数据集划分、模型搭建、Logistic回归模型、随机森林模型

模型评估：
k折交叉验证、混淆矩阵、ROC曲线

二、内容复现

（一） 数据建模

1.数据载入及预设

载入相关库

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import Image

%matplotlib inline #设置静态输出图片

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
plt.rcParams['figure.figsize'] = (10, 6)  # 设置输出图片大小

读取数据

data = pd.read_csv('clear_data.csv')
train = pd.read_csv('train.csv')

>>>data.shape,train.shape  #查看数据行列属性
((891, 11), (891, 12))

data.head()

train.head()

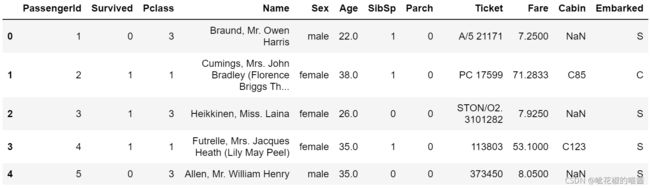
可以看到‘data’相比于‘train’进行了数据清洗，去掉Name和Ticket等字符型数据（对研究意义不大），Sex、Embarked（有多种选项）化为one-hot编码，PassengerId、Survived、Pclass、SibSp、Parch在之前已做数字编码分类处理，文本转为数字有利于提高程序运行速度

2.模型选择与sklearn算法

• 处理完前面的数据我们就得到建模数据，下一步是选择合适模型；
• 在进行模型选择之前我们需要先知道数据集最终是进行监督学习还是无监督学习（判断的直接标准依据这里的data数据集没有最终的被解释变量Survived，因而为无监督学习）；
• 模型的选择一方面是通过我们的任务来决定的；
• 除了根据我们任务来选择模型外，还可以根据数据样本量以及特征的稀疏性来决定；
• 刚开始我们总是先尝试使用一个基本的模型来作为其baseline，进而再训练其他模型做对比，最终选择泛化能力或性能比较好的模型。

这里我们使用机器学习常用库sklearn来完成模型搭建

(1)sklearn简介

Sklearn是什么？
Scikit-learn(sklearn)是机器学习中常用的第三方模块，对常用的机器学习方法进行了封装，包括回归(Regression)、降维(Dimensionality Reduction)、分类(Classfication)、聚类(Clustering)等方法。

官方网站：https://scikit-learn.org/stable/，我们可以登入在线下载该算法包及查询其官方文档与具体函数运用方法。
Sklearn具有以下特点：

• 简单高效的数据挖掘和数据分析工具
• 让每个人能够在复杂环境中重复使用
• 建立NumPy、Scipy、MatPlotLib之上

Sklearn的算法选择路径

由图中，可以看到库的算法主要有四类：分类，回归，聚类，降维。
流程图表示：
蓝色圆圈内是判断条件，绿色方框内是可以选择的算法。我们可以根据自己的数据特征和任务目标去找到一条合适路线，从而完成模型选择。

3.数据集划分

我们对数据集划分切割，为后续评估模型泛化能力做准备，这里使用留出法划分数据集：

• 将数据集分为自变量和因变量
• 按比例切割训练集和测试集(一般测试集的比例有30%、25%、20%、15%和10%)
• 使用分层抽样
• 设置随机种子以便结果能复现

【思考】为什么使用分层抽样，这样的好处有什么？
答：划分的时候要尽可能保证数据分布的一致性，即避免因数据划分过程引入额外的偏差而对最终结果产生影响，所以通常我们采用 分层采样 的方式来对数据进行采样。

sklearn中切割数据集的方法为train_test_split，我们要从data.csv和train.csv中提取train_test_split()所需的参数

X = data
y = train['Survived']

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    X, y, stratify = y,random_state=42)

>>>X_train.shape,X_test.shape #默认情况下训练集的比例约为25%
((668, 11), (223, 11))

X_train.head()  
#当随机种子random_state为整数，在此处多次运行可以验证返回的结果是一样的方便，复现结果；改为0或者没有，则会随机生成

4.模型搭建

(1)创建基于线性模型的分类模型（逻辑回归）

from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier

>>>train['Survived'].value_counts()
0    549
1    342
Name: Survived, dtype: int64

#fit(X,y,sample_weight = None)  其中sample_weight为样本权重，若两类结果数量相差悬殊需要调整一方的权重比例
>>>logr = LogisticRegression().fit(X_train,y_train)
>>>logr
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
          penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
          verbose=0, warm_start=False)
          
>>>logr.score(X_train,y_train) 
0.8068862275449101

#保留三位小数，输出逻辑回归对训练集和测试集的得分
>>>print('训练集得分：{:.3f}'.format(logr.score(X_train,y_train)))
>>>print('测试集得分：{:.3f}'.format(logr.score(X_test,y_test)))
训练集得分：0.807
测试集得分：0.771

下面对参数进行调整

#C为正则化系数的倒数，默认为1，越小越能限制模型的复杂度
>>>logr1 = LogisticRegression(C=0.01).fit(X_train,y_train) 
>>>print('训练集得分：{:.3f}'.format(logr.score(X_train,y_train)))
>>>print('测试集得分：{:.3f}'.format(logr.score(X_test,y_test)))
训练集得分：0.754
测试集得分：0.704

可以看到训练集和测试集的得分均有降低，说明此时模型过于简单欠拟合。

#C为正则化系数的倒数，默认为1，这里C设为1000查看效果
>>>logr2 = LogisticRegression(C=1000).fit(X_train,y_train) 
>>>print('训练集得分：{:.3f}'.format(logr.score(X_train,y_train)))
>>>print('测试集得分：{:.3f}'.format(logr.score(X_test,y_test)))
训练集得分：0.811
测试集得分：0.776

可以看到提高C后相比于上面训练集和测试集的得分均显著提高

(2)创建基于树的分类模型（决策树、随机森林）

• 决策树包含根节点、内部节点和叶节点。根节点包含样本的全集，内部节点对应特征的属性测试，叶节点代表决策的结果，在树的内部节点用某一个属性值进行判断，依次递推，直到这些判断结果到达叶节点。下图为一个简单的决策树：
  
• 随机森林由多颗决策树组成，不同决策树之间没有联系。当进行分类任务时，森林中的每颗决策树都分别对子样本进行判断和分类，每颗决策树都会得到各自的分类结果。
  
• 用多个决策树去拟合数据集的各个子样本时，使用平均值来提高预测的精度和防止过拟合。由于每颗决策树都有自己的“想法”和决策偏差，我们通过取平均值来尽量消除偏差和抵消过拟合。

ranf = RandomForestClassifier().fit(X_train,y_train) 
print('训练集得分：{:.3f}'.format(ranf.score(X_train,y_train)))
print('测试集得分：{:.3f}'.format(ranf.score(X_test,y_test)))
训练集得分：0.988
测试集得分：0.794

以下对随机森林模型进行调参

• 调整决策树的数量参数

#n_estimaters表示决策树的数量，默认为100.其数量多少影响模型的复杂度
>>>ranf1=RandomForestClassifier(n_estimators=1000).fit(X_train,y_train) 
>>>print('训练集得分：{:.3f}'.format(ranf1.score(X_train,y_train)))
>>>print('测试集得分：{:.3f}'.format(ranf1.score(X_test,y_test)))

训练集得分：1.000
测试集得分：0.789

• 调整最大深度参数

#max_depth为最大深度默认为无，这里设置为5
>>>ranf2 = RandomForestClassifier(max_depth=5).fit(X_train,y_train) 
>>>print('训练集得分：{:.3f}'.format(ranf2.score(X_train,y_train)))
>>>print('测试集得分：{:.3f}'.format(ranf2.score(X_test,y_test)))

训练集得分：0.856
测试集得分：0.771

可以看到训练集的得分显著下降

• 改变抽样放回方式

#bootstrap表示是否放回抽样，默认为True放回，这里设为不放回
>>>ranf3 = RandomForestClassifier(bootstrap=False).fit(X_train,y_train) 
>>>print('训练集得分：{:.3f}'.format(ranf3.score(X_train,y_train)))
>>>print('测试集得分：{:.3f}'.format(ranf3.score(X_test,y_test)))
训练集得分：1.000
测试集得分：0.762

【思考】为什么线性模型可以进行分类任务，背后是怎么的数学关系
答：给出函数f(x)=wTx+b；如果函数值小于0，我们就预测类别-1，如果函数值大于0，我们就预测类别+1。对于所有用于分类的线性模型，这个预测规则都是通用的。对于用于分类的线性模型，决策边界是输入的线性函数。线性分类器是利用直线、平面或超平面来分开两个类别的分类器。

【思考】对于多分类问题，线性模型是怎么进行分类的
答： 线性多分类的本质仍是两两分类(one-vs-all/one-vs-rest)。多分类的问题常常是使用差分策略，通过二分类学习来解决多分类问题，即将多分类问题拆解为多个二分类训练二分类学习器最后通过继承得到结果，最经典拆分策略有三种：“一对一”（OvO）、“一对其余”（OvR）和“多对多”（MvM）。

如下图：

• 右1是将三角形看做是一个分类，将其他所有分类看作是另一个分类，那么就将这个多元分类的模型变成了二元分类，利用这个二元分类预测出三角形的概率，即是y=1的概率。
• 右2是将长方形看做是一个分类，将其他所有分类看作是另一个分类，那么就将这个多元分类的模型变成了二元分类，利用这个二元分类预测出长方形的概率，即是y=2的概率。
• 右3是将叉号看做是一个分类，将其他所有分类看作是另一个分类，那么就将这个多元分类的模型变成了二元分类，利用这个二元分类预测出叉号的概率，即是y=3的概率。
• 分别将这些概率算出来之后，怎么知道我们的预测值是哪个呢？答案是选择这些概率中的最大值作为预测值。
  

5. 输出模型预测结果

• 输出模型预测分类标签

>>>pred = logr.predict(X_train)
>>>pred[:10]
array([1, 0, 0, 1, 1, 1, 0, 0, 1, 0], dtype=int64)

• 输出不同分类标签的预测概率

>>>logr.predict_proba(X_train)
array([[0.09256248, 0.90743752],
       [0.7013442 , 0.2986558 ],
       [0.8046259 , 0.1953741 ],
       ...,
       [0.69026636, 0.30973364],
       [0.68640254, 0.31359746],
       [0.90533008, 0.09466992]])

【思考】预测标签的概率对我们有什么帮助
答：可以依概率来判断最后输出的结果有多大程度可以信任，如上举例array第一个数为1的预测概率为0.907，大概率可以认为此对象为幸存乘客。

（二）模型评估

根据之前的模型的建模，我们知道如何运用sklearn这个库来完成建模，以及我们知道了的数据集的划分等等操作。接下来我们需要对模型进行评估，以了解模型的泛化能力和可靠性。

1.交叉验证

• 交叉验证（cross-validation）是一种评估泛化性能的统计学方法，它比单次划分训练集和测试集的方法更加稳定、全面。
• 在交叉验证中，数据被多次划分，并且需要训练多个模型。
• 最常用的交叉验证是 k 折交叉验证（k-fold cross-validation），其中 k 是由用户指定的数字，通常取 5 或 10。
  
  上图示意5折交叉验证，即数据分为五等份，其中四份作训练集一份作测试集，对每份数据依此处理。
• 用10折交叉验证来评估之前的逻辑回归模型

from sklearn.model_selection import cross_val_score
logr = LogisticRegression()

>>>score = cross_val_score(logr,X_train,y_train,cv=10)
>>>score
array([0.80882353, 0.72058824, 0.7761194 , 0.73134328, 0.91044776,
       0.76119403, 0.87878788, 0.78787879, 0.83333333, 0.77272727])

• 计算交叉验证精度的平均值

>>>score.mean()
0.7981243515045094

【思考】k折越多的情况下会带来什么样的影响？
答：数据分为k等份即为k折交叉验证，k越大越能提高模型的稳定性，但同时加重程序的计算负担

2.混淆矩阵

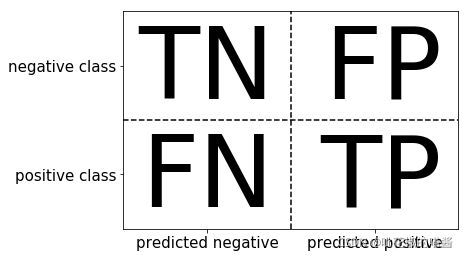
从图中可以得出，行表示实际值，列表示预测值预测结果可以分为如下四类：

• TN-True Negative 真的负类 负类预测为负类，即真阴性；
• FP-False Positive 假的负类 正类预测为负类，即假阴性；
• FN-False Negative 假的正类 负类预测为正类，即假阳性；
• TP-True Positive 真的正类 正类预测为正类，即真阳性
  
  相关指标
• 准确率 (Accuracy)=正确预测数/总样本
• 精确度（Precision）=真阳性/(真阳性+假阳性)（预测为阳性的样本）
• 召回率(Recall)=真阳性/(真阳性+假阴性)（实际为阳性的样本）
• f-分数(F-score)=(精确率和召回率的调和平均数)

以逻辑回归为例

• 混淆矩阵的方法在sklearn中的sklearn.metrics模块
• 混淆矩阵需要输入真实标签和预测标签
• 精确率、召回率以及f-分数可使用classification_report模块

#加载相关库
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report

#计算混淆矩阵
>>>logr = LogisticRegression().fit(X_train,y_train)
>>>y_pred = logr.predict(X_train)
>>>confusion_matrix(y_train,y_pred,labels=[0,1])
array([[357,  55],
       [ 74, 182]], dtype=int64)

>>>y_train.value_counts(), 375+55, 74+182
(0    412
 1    256
 Name: Survived, dtype: int64, 430, 256)

由上结果：0表示死亡，1表示幸存；行表示实际值，列表示预测值；输出的混淆矩阵表示逻辑回归模型对死亡乘客成功预测了357人，剩下55人预测错；幸存乘客成功预测了182人，剩下74人没有被预测到。

#计算精确率、召回率以及f-分数
>>>print(classification_report(y_train,y_pred))
             precision    recall  f1-score   support

          0       0.83      0.87      0.85       412
          1       0.77      0.71      0.74       256

avg / total       0.81      0.81      0.81       668

3.ROC曲线

【思考】什么是ROC曲线，ROC曲线的存在是为了解决什么问题？
答：在信号检测理论中，接收者操作特征曲线(receiver operating characteristic，或称ROC曲线)是一种坐标图式的分析工具，用于选择最佳的信号侦测模型，在同一模型中设定最佳阈值。

• 绘制ROC曲线

ROC曲线的横坐标是假正例率(FPR)，纵坐标是真正例率(TPR)，其中,
TPR= (TP+FN)/TP =正类的召回率
FPR= (TN+FP)/FP =1−负类召回率

from sklearn.metrics import roc_curve

#fpr即坐标轴横轴false postive function;
#tpr即坐标轴纵轴true positive function；
#thresholds为判断正负类的边界值
fpr,tpr,thresholds = roc_curve(y_test,logr.decision_function(X_test))
fpr,tpr,thresholds

plt.plot(fpr,tpr)
plt.xlabel('False Positive Function')
plt.ylabel('True Positive Function')

我们需要找到最接近于0的阈值

np.abs(thresholds)

np.argmin(np.abs(thresholds))
27

plt.plot(fpr,tpr)
plt.xlabel('False Positive Function')
plt.ylabel('True Positive Function')
close_zero = np.argmin(np.abs(thresholds))
plt.plot(fpr[close_zero],tpr[close_zero],'o')
plt.title('LR ROC')

我们还可以直接调用plot_roc_curve方法，同时，绘制不同调参情境下的ROC进行对比：

from sklearn.metrics import plot_roc_curve

logr = LogisticRegression().fit(X_train,y_train)
logr1 = LogisticRegression(C=1000).fit(X_train,y_train)
logr2 = LogisticRegression(class_weight = 'balanced').fit(X_train,y_train)

lr_display = plt_roc_curve(logr,X_test,y_test,name='LR',response_method = 'decision function')
plt_roc_curve(logr1,X_test,y_test,name='LR2',response_method = 'decision function',ax = lr_display.ax_)
plt_roc_curve(logr2,X_test,y_test,name='LR3',response_method = 'decision function',ax = lr_display.ax_)
这里的response_method 我们仍然用逻辑回归中的decision function方法，末尾的ax参数表示在第一张图的基础上进行叠加。

图中AUC即表示曲线与下面坐标轴围成的面积，由于ROC曲线下面所包围的面积越大越好，可以看出LR2模型的效果最好。

参考文章

• Python之Sklearn使用教程
• sklearn库的学习
• ROC曲线学习总结
• 关于混淆矩阵以及分类问题的概述
• sklearn画ROC曲线方法总结1（plot_roc_curve）
• Machine Learning第三讲[Logistic回归] --（二）Logistic回归模型
• Machine Learning第三讲[Logistic回归] --（三）多元分类