深度学习笔记---数值微分版 对MNIST数据集的二层神经网络的学习实现

# 1.神经网络的学习前提和步骤

前提

神经网络存在合适的权重和偏置。

步骤一（挑选mini-batch）

从训练数据中随机选出一部分数据，这部分数据称为mini-batch。
我们的目标是减少mini-batch这部分数据的损失函数的值。

步骤二（计算梯度）

为了减小mini-batch这部分数据的损失函数的值，需要求出有关各个权重参数的梯度。

步骤三（更新参数）

将权重参数沿梯度方向进行微小更新。

步骤四（重复）

重复步骤1,2,3

# 2.二层神经网络类的实现

上一篇博客已经实现了一层神经网络类，这里二层神经网络类的实现与其类似。

import sys,os
sys.path.append(os.pardir)
import numpy as np
from ch03.sigmoid import sigmoid
from ch03.softmax import softmax
from cross_entropy_error import cross_entropy_error
from numerical_gradient import numerical_gradient

# 二层神经网络类
class TwoLayerNet:
	
	def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):   # 构造函数__init__，第1个参数为该函数正在创建的对象，
								                          # 第2、3、4个参数依次表示输入层、隐藏层、输出层的神经元数
								                          # 第5个参数表示权重初始化水平（这里设置为0.01）
		# 初始化权重参数
		self.params = {}   # 成员变量params的初始化，params是一个字典型变量
		
		self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)  # 设置标识W1为第一层权重，randn函数返回一个input_size*hidden_size的二维数组，数据符合高斯分布
		self.params['b1'] = np.zeros(hidden_size)                                       # 设置标识b1为第一层偏置，zeros函数返回一个由hidden_size个0组成的一维数组
		
		self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
		self.params['b2'] = np.zeros(output_size)

	def predict(self, x):                                                             # 推理函数predict，第1个参数为正在调用该函数的对象，第2个参数为输入数据（输入层神经元）
		W1,W2 = self.params['W1'],self.params['W2']                                     # 设置局部变量W1，W2，b1，b2，用实例变量params分别为其赋值
		b1,b2 = self.params['b1'],self.params['b2']
		
		a1 = np.dot(x,W1) + b1                                                          # 计算加权和a1
		z1 = sigmoid(a1)                                                                # 通过激活函数sigmoid将a1转换为信号z1
		a2 = np.dot(z1,W2) + b2                                                         # 计算加权和a2
		y = softmax(a2)                                                                 # 通过输出层激活函数softmax将a2转换为输出信号y
		
		return y
	
	# x:输入数据，t:监督数据
	def loss(self, x, t):                                                             # 损失函数loss，第1个参数为正在调用该函数的对象，第2、3个参数分别为输入数据，和与输入数据对应的正确解标签
		y = self.predict(x)                                                             # 调用实例方法predict将输入数据x转换为推理结果y
		return cross_entropy_error(y,t)                                                 # 通过交叉熵误差函数，根据推理结果和正确解标签计算出损失函数值，并返回
		
	def accuracy(self, x, t):                                                         # 精度函数accuracy，参数同loss
		y = self.predict(x)                                                             # 调用实例方法predict将输入数据x转换为推理结果y
		y = np.argmax(y, axis=1)                                                        # 记录y每一行最大值的下标形成一个数组，即推理结果的简单表示
		t = np.argmax(t, axis=1)                                                        # 记录t每一行最大值的下标形成一个数组，即正确结果的简单表示
		
		accuracy = np.sum(y == t)/float(x.shape[0])                                     # y == t形成一个boolean型数组，True表示识别正确，sum(y == t)得到True的个数，即正确识别的图像数目。除以图像总数目得到识别精度。
		return accuracy
		
	def numerical_gradient(self,x,t):                                                 # 普通梯度函数numerical_gradient，参数同loss
		loss_W = lambda W: self.loss(x,t)                                               # 定义一个简单局部函数loss_W，W为其伪参数，该函数内容即调用实例函数loss，并返回其返回值
		
		grads  = {}                                                                     # 定义一个局部变量grads，grads为一个字典型变量，表示梯度数组，用于存放各参数的梯度
		grads['W1'] = numerical_gradient(loss_W, self.params['W1'])                     # 通过导入的梯度函数，计算W1的梯度，存放在grads['W1']
		grads['b1'] = numerical_gradient(loss_W, self.params['b1'])                     # 计算并存放b1
		grads['W2'] = numerical_gradient(loss_W, self.params['W2'])                     # 计算并存放W2
		grads['b2'] = numerical_gradient(loss_W, self.params['b2'])                     # 计算并存放b2
		
		return grads

# 2.对MNIST数据集的学习与评价

下面我们会利用上面实现的二层神经网络类，来具体实现对MNIST数据集的学习。

下面代码中的epoch是一个单位，设置为600次更新。对于每个epoch，我们会计算并记录一次训练数据的识别精度和测试数据的识别精度。在所有更新次数（设置为10000）完成后，会绘制出一张识别精度变化图。我们会根据这张图得出对此次学习的评价。

import sys,os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
import matplotlib.pyplot as plt


# 以二层神经网络类TwoLayerNet为对象，使用MNIST数据集进行学习

(x_train, t_train),(x_test, t_test) = load_mnist(normalize = True, one_hot_label = True) # 取出MNIST数据集

train_acc_list = []   # 定义一个列表变量，用于记录每个epoch，训练数据的精度
test_acc_list = []    # 定义一个列表变量，用于记录每个epoch，测试数据的精度



# 超参数
iters_num = 10000              # 定义变量iters_num用于表示更新次数（这里设置为10000）
train_size = x_train.shape[0]  # 定义变量train_size用于表示训练数据总数目（即60000）
batch_size = 100               # 定义变量batch_size用于表示每次使用的批数据的大小（这里设置为100）
learning_rate = 0.1            # 定义变量learning_rate用于表示学习率的大小（这里设置为0.1）

iter_per_epoch = max(train_size / batch_size, 1) # 这里定义每个epoch的大小，实际定义为600，以后每更新600次，计算一次训练数据和测试数据的识别精度
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10) # 创建一个二层神经网络类TwoLayerNet的对象network，这里定义的入口参数是用于设置权重参数的形状的。这里的784对应一张图像的784个像素，10对应数字0到9的10个类别，50是可更改的设定。

for i in range(iters_num):     # for循环i从0到9999（更新10000次）
	# 获取mini-batch
	batch_mask = np.random.choice(train_size, batch_size)  # 从0到59999随机选择100个值存至数组batch_mask
	x_batch = x_train[batch_mask]                          # 把数组batch_mask的值作为数组x_train的下标，取出对应元素形成数组x_batch
	t_batch = t_train[batch_mask]                          # 把数组batch_mask的值作为数组t_train的下标，取出对应元素形成数组t_batch
	
	# 计算梯度
	grad = network.numerical_gradient(x_batch, t_batch)    # 利用数值微分，计算出损失函数关于各个权重参数的梯度 
	
	# 更新参数
	for key in ('W1','b1','W2','b2'):                      # 将每个参数依次根据各自的梯度进行微小更新
		network.params[key] -= learning_rate * grad[key]
	
	print(i,"次更新已经完成")	
	
	if i % iter_per_epoch == 0:                            # 对于每个epoch
		train_acc = network.accuracy(x_train, t_train)     # 计算训练数据的识别精度
		test_acc = network.accuracy(x_test, t_test)        # 计算测试数据的识别精度
		train_acc_list.append(train_acc)                   # 将计算出的识别精度存放至各自的列表
		test_acc_list.append(test_acc)
	
# 绘制图形
x = np.arange(len(train_acc_list))                                       # 设置x为精度数组下标
plt.plot(x, train_acc_list, label='train acc')                           # 以训练数据精度数组的值为y,绘制标签为'train acc'的曲线
plt.plot(x, test_acc_list, label='test acc', linestyle='--')             # 以测试数据精度数组的值为y,用虚线绘制标签为'test acc'的曲线
plt.xlabel("epochs")                                                     # 设置x轴标签为"epochs"
plt.ylabel("accuracy")                                                   # 设置y轴标签为"accuracy"
plt.ylim(0, 1.0)                                                         # 设置y轴的范围为0到1
plt.legend(loc='lower right')                                            # 设置图例，控制其在图像右下角
plt.show()                                                               # 显示图像

上述数值微分版学习的实现，会使用很长很长的时间...

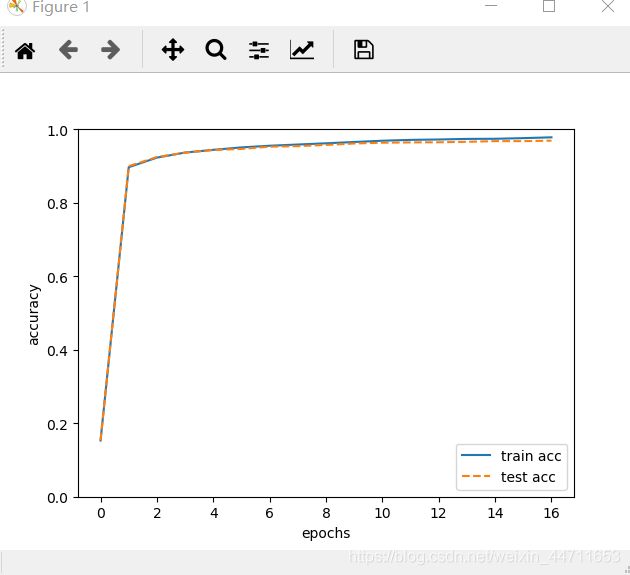
最后得到的识别精度变化图如下

从上图可知，训练数据和测试数据的识别精度变化曲线基本吻合，说明没有发生过拟合现象（过拟合是指仅能正确识别训练数据中的图像）。识别精度的逐步上升，说明此次学习是有效的。

最后还是要提一下，由于此次试验使用的是批数据（输入输出数据均变成二维的），所以之前的softmax函数在维度控制方面作了如下修改

def softmax(x):
    if x.ndim == 2:                                # 当输入的加权和是二维数据时
        x = x.T                                    # 转置是为了后面的广播功能能正确进行
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T                                 # 将结果转置回去，恢复正常形状

    x = x - np.max(x) # 溢出对策
    return np.exp(x) / np.sum(np.exp(x))

 

# 本博客参考了《深度学习入门——基于Python的理论与实现》（斋藤康毅著，陆宇杰译），特在此声明。