NOTE(三):Deep Learning
摘要:对弯月形数据进行分类,结构采用一层隐层三个神经元,并与一层隐层两个神经元和两层隐层两个神经元进行对比。
一、弯月形数据
二、结构
1. 1x3
2. 2x2
三、 1x3代码(python)
1.绘制弯月形数据
import numpy as np
import matplotlib.pyplot as plt
import math
pi=math.pi
x1=np.arange(0,pi,0.01)
x2=np.arange(pi,2*pi,0.01)
num1=np.size(x1)
noise1=np.random.uniform(-0.1,0.5,num1)
noise2=np.random.uniform(-0.5,0.1,num1)-0.5
y1=np.sin(x1)+noise1
y2=np.sin(x2)+noise2+1
plt.scatter(x1,y1)
plt.scatter(x1+pi/2,y2)
2. 设置子函数
# 子函数
# 设置激活函数
#def sigmoid(x):
#sigmoid=1/(1+np.exp(-1*x))
#return(sigmoid)
#print(sigmoid(0))
# https://www.cnblogs.com/zhhy236400/p/9873322.html
def sigmoid(inx):
if inx>=0: #对sigmoid函数的优化,避免了出现极大的数据溢出
sigmoid=1/(1+math.exp(-inx))
return(sigmoid)
else:
sigmoid=math.exp(inx)/(1+math.exp(inx))
return(sigmoid)
print(sigmoid(1))
def dsigmoid(x):
dsigmoid=sigmoid(x)*(1-sigmoid(x))
return(dsigmoid)
# 设置标签函数
def T(i):
if i<=num1:
T=0
else:
T=1
return(T)
print(T(70))
0.7310585786300049
0
3. 提取数据
X1=np.array(x1)
Y1=np.array(y1)
Y2=np.array(y2)
X=[[X1,Y1],[X1,Y2]]
X=np.hstack(X)
XT=X.T
print(np.shape(XT))
(630, 2)
(2, 1, 63)
4. 初始化
#初始化
N=10000
w=np.array([[-0.001,0.021],[0.003,-0.04],[0.005,-0.06]])# w:3x2
b=np.array([[0],[0],[0]])# b:3x1
v=np.array([[0.01],[-0.02],[0.03]])# v:3x1
c=0
sum_w=np.zeros((3,2))
sum_b=np.zeros((3,1))
sum_v=np.zeros((3,1))
sum_c=0
eta=0.01
fp=np.zeros((1,3))
p=np.matmul(w,X[...,1])
print(np.shape(X[...,1]))
print(X[...,1])
print(p)
print(np.transpose(p))
print(type(p))
print(b)
print(p+np.transpose(b))
print(np.transpose(p+np.transpose(b)))
(2,)
[0.01 0.11268667]
[ 0.00235642 -0.00447747 -0.0067112 ]
[ 0.00235642 -0.00447747 -0.0067112 ]
[[0]
[0]
[0]]
[[ 0.00235642 -0.00447747 -0.0067112 ]]
[[ 0.00235642]
[-0.00447747]
[-0.0067112 ]]
5. 训练权重和偏置
for i in range(N):
#由前往后算各层的值
for j in range(2*num1):
p=np.dot(w,X[...,j])+np.transpose(b)
p=np.transpose(p)
p1=p[0,0]
p2=p[1,0]
p3=p[2,0]
fp[0,0]=sigmoid(p1)
fp[0,1]=sigmoid(p2)
fp[0,2]=sigmoid(p3)
q=np.matmul(np.transpose(v),np.transpose(fp))+c# v:3x1,fp:1x3
y=sigmoid(q)
# 由后往前对权值进行更新
#第二层
delta_v=(T(j)-y)*fp.T
delta_c=(T(j)-y)
#第一层
dq_dp_11=np.dot(v[0,0],dsigmoid(p1))
dq_dp_22=np.dot(v[1,0],dsigmoid(p2))
dq_dp_33=np.dot(v[2,0],dsigmoid(p3))
dq_dp=np.array([[dq_dp_11],[dq_dp_22],[dq_dp_33]])
delta_b=delta_c*dq_dp
#print(np.shape(delta_b))
#print(np.shape(XT[j,...]))
delta_w=np.dot(delta_b, [XT[j,...]])
sum_w=sum_w+delta_w
sum_b=sum_b+delta_b
sum_v=sum_v+delta_v
sum_c=sum_c+delta_c
#print(p)
w=w+sum_w*eta
b=b+sum_b*eta
v=v+sum_v*eta
c=c+sum_c*eta
print(w)
print(b)
#print(v)
#print(c)
#print(DELTA_W)
[[ -107.16125727 11494.14494609]
[ 3866.8373999 -5901.08033082]
[ -191.79916915 -12225.33359158]]
[[ 391.80704726]
[2483.5225647 ]
[5882.97741719]]
Y=np.zeros((1,2*num1))
YY=np.zeros((1,2*num1))
Q=np.zeros((1,2*num1))
FP=np.zeros((2*num1,3))
6. 分类结果
# 分类结果
for j in range(2*num1):
p=np.matmul(w,X[...,j])+np.transpose(b)
p=np.transpose(p)
p1=p[0,0]
p2=p[1,0]
p3=p[2,0]
fp[0,0]=sigmoid(p1)
fp[0,1]=sigmoid(p2)
fp[0,2]=sigmoid(p3)
q=np.matmul(np.transpose(v),np.transpose(fp))+c# v:3x1,fp:1x3
y=sigmoid(q)
Y[0,j]=y
Q[0,j]=q
FP[j,...]=fp
#print(Q)
print(Y)
#print(FP)
[[0. 0.12832229 0.12832229 0.12832229 0.12832229 0.12832229
0.12832229 0.12832229 0. 0.12832229 0.12832229 0.12832229
0.12832229 0.12832229 0.12832229 0.12832229 0.12832229 0.12832229
0.12832229 0. 0. 0.12832229 0. 0.12832229
0. 0. 0. 0.12832229 0.12832229 0.12832229
0. 0.12832229 0. 0.12832229 0. 0.
0. 0.12832229 0. 0. 0.12832229 0.
0.12832229 0. 0. 0. 0. 0.12832229
0. 0.12832229 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0.12832229 0. 0. 0. 0. 0.
0.12832229 0.12832229 0.12832229 0. 0. 0.
0.12832229 0.12832229 0.12832229 0. 0.12832229 0.12832229
0. 0.12832229 0. 0. 0. 0.
0.12832229 0.12832229 0.12832229 0. 0. 0.12832229
0.12832229 0.12832229 0.12832229 0. 0. 0.
0.12832229 0.12832229 0.12832229 0.12832229 0.12832229 0.12832229
0.12832229 0.12832229 0.12832229 0.12832229 0.12832229 0.12832229
0.12832229 0.12832229 0.12832229 0.12832229 0.12832229 0.12832229
0.12832229 0.12832229 0.12832229 0.12832229 0.12832229 0.12832229
0.12832229 1. 0.12832229 1. 0.12832229 1.
0.12832229 0.12832229 1. 0.12832229 0.12832229 0.12832229
0.12832229 1. 1. 0.12832229 0.12832229 0.12832229
1. 0.12832229 1. 0.12832229 0.12832229 1.
1. 0.12832229 1. 1. 0.12832229 0.12832229
0.12832229 1. 1. 0.12832229 1. 1.
0.12832229 1. 1. 1. 0.12832229 1.
0.12832229 1. 0.12832229 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.
1. 0.12832229 1. 1. 0.12832229 1.
1. 1. 1. 1. 1. 1.
1. 0.12832229 1. 1. 0.12832229 0.12832229
1. 0.12832229 0.12832229 1. 1. 1.
0.12832229 0.12832229 0.12832229 0.12832229 0.12832229 1.
1. 0.12832229 1. 0.12832229 0.12832229 0.12832229
1. 1. 0.12832229 0.12832229 0.12832229 0.12832229
0.12832229 0.12832229 1. 1. 1. 0.12832229
0.12832229 0.12832229 0.12832229 0.12832229 0.12832229 0.12832229]]
m1=0
m2=0
for k in range(0,num1-1,1):
if Y[0,k]<0.5:
m1=m1+1
for l in range(0,num1-1,1):
if Y[0,l+num1]>=0.5:
m2=m2+1
prec=(m1+m2)/(2*num1)
print("准确率为:",prec)
print(m1)
print(m2)
准确率为: 0.8904761904761904
314
247
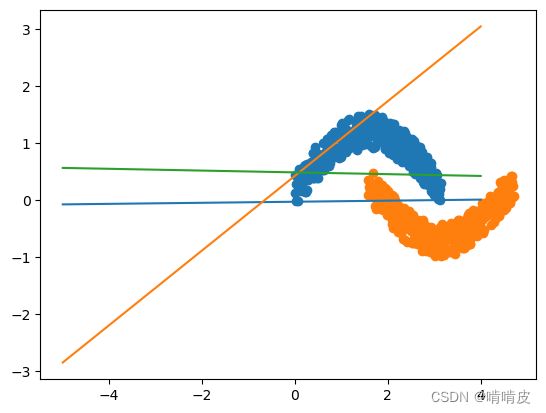
7.绘制结果
x=range(-5,5,1)
Y1=-1*w[0,0]/w[0,1]*x-b[0,0]/w[0,1]
Y2=-1*w[1,0]/w[1,1]*x-b[1,0]/w[1,1]
Y3=-1*w[2,0]/w[2,1]*x-b[2,0]/w[2,1]
plt.scatter(x1,y1)
plt.scatter(x1+pi/2,y2)
plt.plot(x,Y1,label='1')
plt.plot(x,Y2,label='2')
plt.plot(x,Y3,label='3')
plt.show()
四、 不同结构准确率对比(1x3 vs 1x2 vs 2x2)
1. 1x3:
2. 1x2:
3. 2x2
五、总结
1. 准确率
1x3≈2x2>1x2
2. 局限性
1.目前的权重和偏置的初始化都是根据经验设定固定值
2.2x2结构有几率存在梯度消失问题