17届智能车图像处理部分讲解

目录

须知

寻边线

寻拐点

补线

最后

---

须知

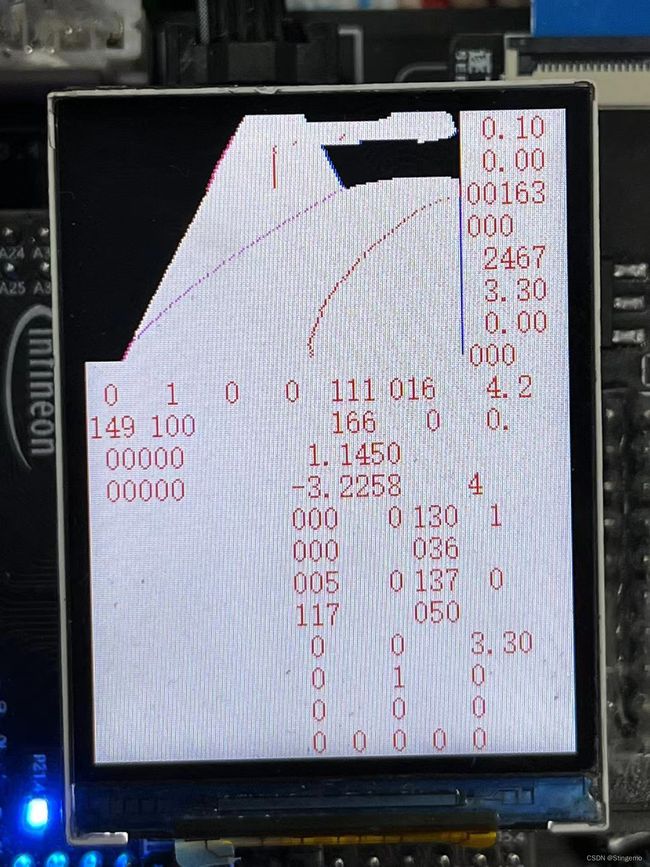
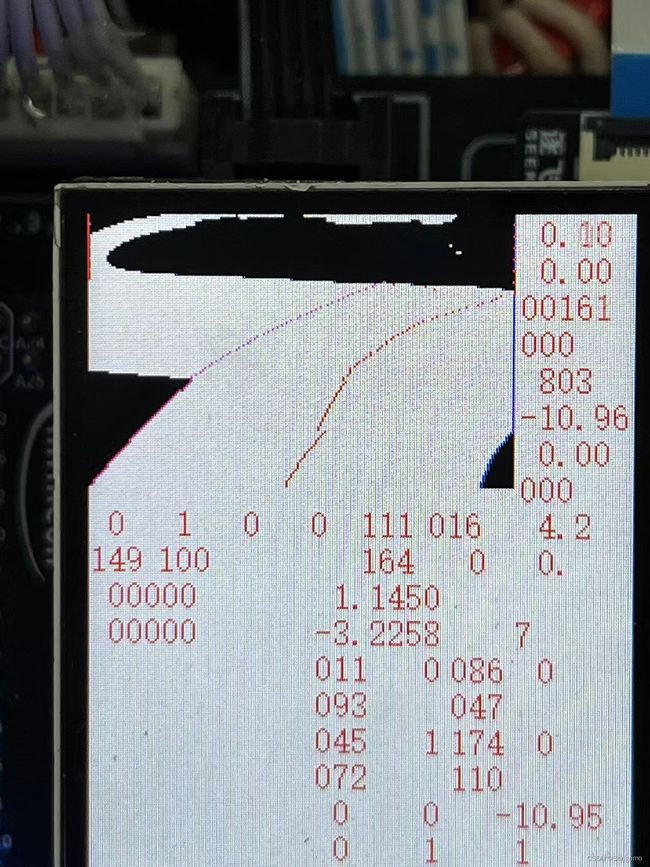
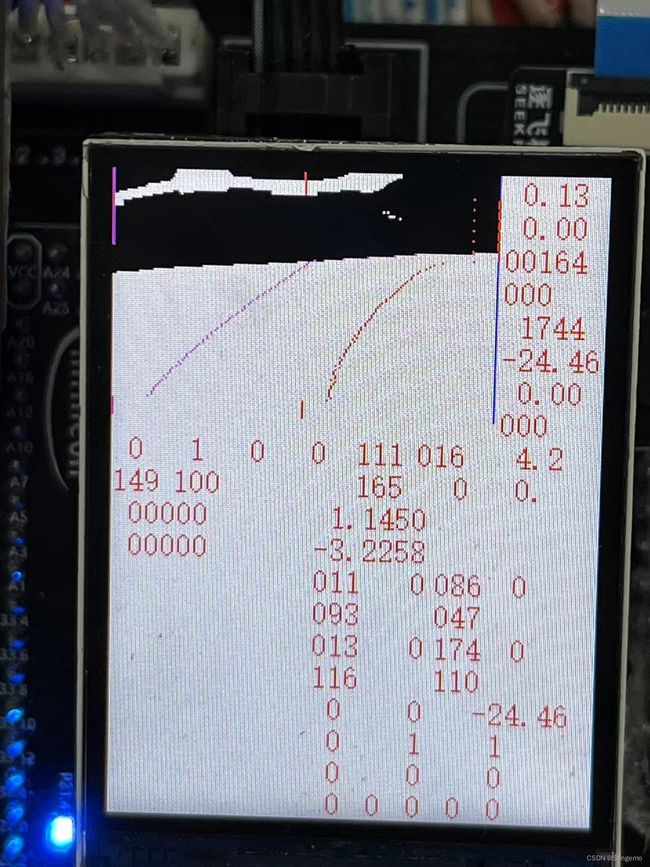
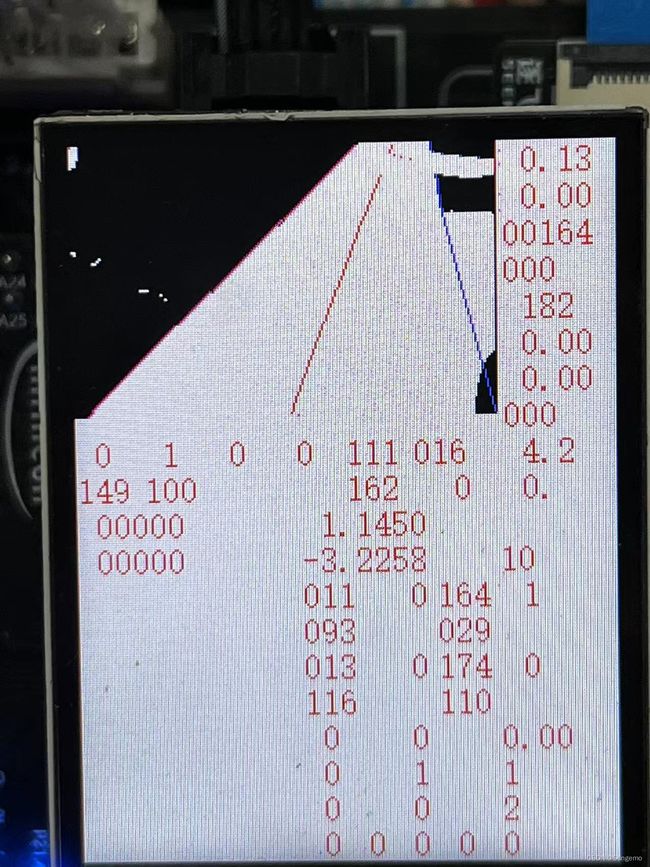
讲解代码使用的摄像头为总钻风摄像头，图像像素为188*120，图像进行了二值化，这里建议如果需要对光线有要求的同学使用灰度处理。没有使用过上位机，展示的图片都是直接拍摄2寸IPS的显示。

寻边线

当我们采集到一帧图像并做完二值化后，我们就开始寻边线，我使用了简单方便的左右扫线，因为在某些情况顶部图像会是黑的，所以使用从图像靠近车头的一端扫线。此时我做了些许处理，如果第一次扫线就从中间开始扫，以后会从上一次计算的中线开始扫，这也需要每次扫完一行就得计算一下中线。为了更加符合赛道变化，下一行的扫描起始点是上一行的中线，当然某些特殊情况也会出问题，比如遇到斑马线，所以又必须对斑马线做处理。左右扫线简单方便，但是执行起来需要遍历的数据量比较多。

//-------------------------------------------------------------------------------------------------------------------
//  @brief      左右巡边线
//  @param      BoundaryRight   右丢线行数
//  @param      BoundaryLeft    左丢线行数 
//  @param
//  @param
//  @return     void
//  @note       采用左右扫线的方法，从图像最低端开始，每行扫完会计算一次中线，下一行扫描从上一行中线开始
//-------------------------------------------------------------------------------------------------------------------
static uint8 star = 93;                             //寻线初始点
//需优化：有时其他赛道会干扰
//如果当左边线寻到有边界则使以后边线都处于边界
void Get_Line(void)
{
//    float k=0;  //斜率
//    float b=0;  //截距
    //uint8 left=0;
    //int kuan=0;
//    k=((float)xtwo - (float)xone)/((float)ytwo - (float)yone);
//    b=(float)yone - ((float)xone*k);
    BoundaryRight = 0;
    BoundaryLeft = 0;
    if(Middle_Black_Point[119] == 0 || Middle_Black_Point[119] == 187)  //判断起始点是否在图像中间
    {
        star = 93;
    }
    else
    {
        star = Middle_Black_Point[119];
    }
    for(uint8 y=119;y>=0;y--)
    {
        for(uint8 x=star;x<188;x++)
        {
            if(Emo_imag[y][x]==EmoBlack)  //黑黑黑即判断为边线
            {
                if(Emo_imag[y][x+1]==EmoBlack && Emo_imag[y][x+2]==EmoBlack)
                {
                    if(y < Endline )
                        Right_Black_Point[y] = 187;
                    else
                        Right_Black_Point[y]=x;
                    //left=star;
                    break;
                }
            }
            if(x==186)                      //有点问题，返校复查
            {
                Right_Black_Point[y]=187;
                //left=star;
                if(y > Endline && y < 108)
                    BoundaryRight++;
                break;
            }
        }
        for(uint8 x=star;x>=0;x--)
        {
            if(Emo_imag[y][x]==EmoBlack)
            {
                if(Emo_imag[y][x-1]==EmoBlack && Emo_imag[y][x-2]==EmoBlack)
                {
                    if(y < Endline)
                        Left_Black_Point[y] = 0;
                    else
                        Left_Black_Point[y]=x;
                    break;
                }
            }
            if(x==0)
            {
                Left_Black_Point[y]=0;
                if(y > Endline && y < 108)
                    BoundaryLeft++;
                break;
            }
        }
        if(Right_Black_Point[y]==187&&Left_Black_Point[y]==0)        //两边都没找到线
        {
            Middle_Black_Point[y]=Middle_Black_Point[y+1];
            //star=Middle_Black_Point[y];
            star = 93;
        }
        else if(Right_Black_Point[y]==187&&Left_Black_Point[y]!=0)    //左边找到线
        {
            Middle_Black_Point[y]=Left_Black_Point[y]+Straight[y];
            star=Middle_Black_Point[y];
//            if(CurvatureRight < -0.0045)
//            {
//                kuan = ((y-120)*(y-120)/(20)+93);
//                kuan = kuan > (187-Right_Black_Point[y]) ? (187-Right_Black_Point[y]) : kuan;
//                Middle_Black_Point[y]=Left_Black_Point[y]+kuan;
//            }
        }
        else if(Left_Black_Point[y]==0&&Right_Black_Point[y]!=187)    //右边找到线
        {
            Middle_Black_Point[y]=Right_Black_Point[y]-Straight[y];
            star=Middle_Black_Point[y];
//            if(CurvatureRight < -0.0045)
//            {
//                kuan = ((y-120)*(y-120)/(20)+93);
//                kuan = kuan > Right_Black_Point[y] ? Right_Black_Point[y] : kuan;
//                Middle_Black_Point[y]=Right_Black_Point[y]-kuan;
//            }
        }
        else             //两边都找到线
        {
            Middle_Black_Point[y]=(uint8)(((int)Right_Black_Point[y]+(int)Left_Black_Point[y])/2);
            star=Middle_Black_Point[y];
        }
//        Middle_Black_Point[y] = Middle_Black_Point[y] < 1 ? 1 : Middle_Black_Point[y];
//        Middle_Black_Point[y] = Middle_Black_Point[y] > 186 ? 186 : Middle_Black_Point[y];
        Middle_Black_Point[y] = Middle_Black_Point[y] < 1 ? 0 : Middle_Black_Point[y];
        Middle_Black_Point[y] = Middle_Black_Point[y] >186 ? 187 :Middle_Black_Point[y];
        if(y==0)
            break;
    }
    //star = Middle_Black_Point[119];
}

寻拐点

寻拐点呢我采用了类似于八邻域的原理，首先是下拐点，我们从底端向上寻找，因为拐点对应的一定是丢线的，所以向上一直寻找到丢线行，以丢线行再向下对一个个点进行判断。

以右下拐点为例，我们放大像素块，我们从红点像素块的左下开始以顺时针旋转，当扫描的点周边的八个像素块出现四个白色像素块时即满足拐点。但是需要注意，拐点是不会距离丢线行数太多的，为了防止拐点误判的出现，我们应限制以丢线行数进行扫描的次数。前边说过左右扫线会因为斑马线造成干扰，所以扫寻完下拐点后，上拐点选择从图像上端向下扫，同样是向下扫到丢线后向再向上寻点，当然，对于扫描点附近八个像素块的旋转就应该换个方向。

//-------------------------------------------------------------------------------------------------------------------
//  @brief      拐点寻找
//  @param      findlcount   拐点距离丢线的行数，用于判断大小圆环，和区分P字和圆环
//  @param
//  @param
//  @param
//  @return     void
//  @note       采用5邻域的原理寻找拐点，下拐点从图像低端往上扫，上拐点从图像上方向下扫，左右扫线会在斑马线出现问题，
//-------------------------------------------------------------------------------------------------------------------
void Identify(void)
{
    uint8 findr_x = 0;    //右点
    uint8 findr_y = 0;
    uint8 examr_x = 0;
    uint8 examr_y = 0;
    uint8 findl_x = 0;    //左点
    uint8 findl_y = 0;
    uint8 examl_x = 0;
    uint8 examl_y = 0;
    uint8 star = 0;
    uint8 end = 0;
    uint8 examcount = 0;
    //uint8 count;
    //uint8 examerror;
//    uint8 dircount;
    int directionrd[5][2] =  {{-1,1}, {-1,0}, {-1,-1}, {0,1}, {1,1}};  //顺时针下方向数组先x再y
    int directionld[5][2] =  {{1,1}, {1,0}, {1,-1}, {0,-1}, {-1,-1}};  //逆时针下方向数组
    int directionru[5][2] =  {{1,1}, {0,1}, {-1,1}, {-1,0}, {-1,-1}};  //逆时针上方向数组
    int directionlu[5][2] =  {{-1,1}, {0,1}, {1,1}, {1,0}, {1,-1}};  //逆时针上方向数组

    //每次采集后都对拐点标志位清零
    if(Right_Up_Point_finish_flag == 1)
        Right_Up_Point_finish_flag = 0;
    if(Left_Up_Point_finish_flag == 1)
        Left_Up_Point_finish_flag = 0;
    if(Right_Down_Point_finish_flag == 1)
        Right_Down_Point_finish_flag = 0;
    if(Left_Down_Point_finish_flag == 1)
        Left_Down_Point_finish_flag = 0;
    for(uint8 y = 105 ; y >= 30 ; y--)
    {
        if(Right_Down_Point_finish_flag == 0)
        {
            if(y > Endline && Right_Black_Point[y-1]==187 && Right_Black_Point[y-2]==187 && Emo_imag[y][Right_Black_Point[y]-6] == EmoWhite
               && y > Endline && Emo_imag[y-2][Right_Black_Point[y]] == EmoWhite && Emo_imag[y-5][Right_Black_Point[y]] == EmoWhite)    //右下拐点
            {
                star=y;
                for(uint8 y=star;y<=(star+18);y++)
                {
                    if(Right_Black_Point[y]<184 && Emo_abs(Right_Black_Point[y+1]-Right_Black_Point[y])<3
                    && Emo_abs(Right_Black_Point[y+2]-Right_Black_Point[y])<4)
                    {
                        findr_x=Right_Black_Point[y];
                        findr_y=y;
                        for(uint8 dircount = 0;dircount<5;dircount++)
                        {
                            examr_x=findr_x+directionrd[dircount][0];
                            examr_y=findr_y+directionrd[dircount][1];
                            if(Emo_imag[examr_y][examr_x]==255)
                            {
                                examcount++;
                            }
                        }
                        if(examcount >= 4)
                        {
                            examcount=0;
                            Right_Down_Point[0]=findr_x;
                            Right_Down_Point[1]=findr_y;
//                            if(Last_Right_Point[0] == 0)
//                            {
//                                Last_Right_Point[0] = Right_Down_Point[1];
//                            }
//                            if(Emo_Uint8_dec(Right_Down_Point[1],Last_Right_Point[0]) < -15)
//                            {
//                                Right_Down_Point_finish_flag = 0;
//                            }
//                            else
//                            {
                                Right_Down_Point_finish_flag = 1;
//                                Last_Right_Point[0] = Right_Down_Point[1];
//                            }
    //                        findrcount = (int)y-(int)star;
                            break;
                        }
                        else
                        {
                            Right_Down_Point_finish_flag = 0;
                            examcount=0;
                        }
                    }
                    if(y==100)
                    {
                        Right_Down_Point_finish_flag=0;
                    }
                }
            }
        }
        if(Left_Down_Point_finish_flag == 0)
        {
            if(y > Endline && Left_Black_Point[y-1]==0 && Left_Black_Point[y-2]==0 && Emo_imag[y][Left_Black_Point[y]+6] == EmoWhite
               && y > Endline && Emo_imag[y-2][Left_Black_Point[y]] == EmoWhite && Emo_imag[y-5][Left_Black_Point[y]] == EmoWhite)     //左下拐点
            {
                star=y;
                for(uint8 y=star;y<=(star+18);y++)
                {
                    if(Left_Black_Point[y]>4 && Emo_abs(Left_Black_Point[y+1]-Left_Black_Point[y])<3
                       && Emo_abs(Left_Black_Point[y+2]-Left_Black_Point[y])<4)
                    {
                        findl_x=Left_Black_Point[y];
                        findl_y=y;
                        for(uint8 dircount = 0;dircount<5;dircount++)
                        {
                            examl_x=findl_x+directionld[dircount][0];
                            examl_y=findl_y+directionld[dircount][1];
                            if(Emo_imag[examl_y][examl_x]==255)
                            {
                                examcount++;
                            }
                        }
                        if(examcount>=4 )
                        {
                            examcount=0;
                            Left_Down_Point[0]=findl_x;
                            Left_Down_Point[1]=findl_y;
//                            if(Last_Left_Point[0] == 0)
//                            {
//                                Last_Left_Point[0] = Left_Down_Point[1];
//                            }
//                            if(Emo_Uint8_dec(Left_Down_Point[1],Last_Left_Point[0]) < -15)
//                            {
//                                Left_Down_Point_finish_flag = 0;
//                            }
//                            else
//                            {
                                Left_Down_Point_finish_flag = 1;
//                                Last_Left_Point[0] = Left_Down_Point[1];
//                            }
    //                        findlcount = y-star;
                            break;
                        }
                        else
                        {
                            Left_Down_Point_finish_flag = 0;
                            examcount=0;
                        }
                    }
                    if(y==100)
                    {
                        Left_Down_Point_finish_flag=0;
                    }
                }
            }
        }
//        if(CrossLeft_Down_Point_finish_flag==1 && CrossRight_Down_Point_finish_flag==1)
//        {
//            break;
//        }
    }
    if(Left_Down_Point_finish_flag==1 && Right_Down_Point_finish_flag==1)
        end=Right_Down_Point[1];
    else if(Left_Down_Point_finish_flag==1)
        end=Left_Down_Point[1];
    else if(Right_Down_Point_finish_flag==1)
        end=Right_Down_Point[1];
    else
        end=94;
    for(uint8 y=20;y<=end;y++)
    {
        if(Right_Up_Point_finish_flag == 0)
        {
            if(y > Endline && Right_Black_Point[y+1]==187 && Right_Black_Point[y+2]==187 && Right_Black_Point[y+3]==187)   //右上拐点
            {
               star=y;
               for(uint8 y=star;y>=(star-22);y--)
               {
                   if(Right_Black_Point[y]<180 && Emo_abs(Right_Black_Point[y-1]-Right_Black_Point[y])<4
                   && Emo_abs(Right_Black_Point[y-2]-Right_Black_Point[y])<4 && Emo_imag[y][Right_Black_Point[y]-6] == EmoWhite
                   && Emo_imag[y-1][Right_Black_Point[y-1]-5] == EmoWhite && Emo_imag[y-2][Right_Black_Point[y]-5] == EmoWhite
                   && Emo_imag[y-3][Right_Black_Point[y]-5] == EmoWhite && Right_Black_Point[y] > Middle_Black_Point[y] && Emo_imag[y+3][Right_Black_Point[y]] == EmoWhite
                   && Emo_imag[y+5][Right_Black_Point[y]] == EmoWhite && Emo_imag[y+7][Right_Black_Point[y]] == EmoWhite)
                   {
                       findr_x=Right_Black_Point[y];
                       findr_y=y;
                       for(uint8 dircount = 0;dircount<5;dircount++)
                       {
                           examr_x=findr_x+directionru[dircount][0];
                           examr_y=findr_y+directionru[dircount][1];
                           if(Emo_imag[examr_y][examr_x]==255)
                           {
                               examcount++;
                           }
                       }
                       if(examcount>=4 && findr_y >Endline)
                       {
                           examcount=0;
                           Right_Up_Point[0]=findr_x;
                           Right_Up_Point[1]=findr_y;
                           if(Last_Right_Point[1] == 0)
                           {
                               Last_Right_Point[1] = Right_Up_Point[1];
                           }
                           if(Right_Up_Point[1] < 16)
                           {
                               Right_Up_Point[1] = Last_Right_Point[1];
                               Right_Up_Point_finish_flag = 0;
                           }
                           else
                           {
                               Right_Up_Point_finish_flag = 1;
                               Last_Right_Point[1] = Right_Up_Point[1];
                           }
                           findrcount=(int)star-(int)findr_y;
                           break;
                       }
                       else
                       {
                           Right_Up_Point_finish_flag = 0;
                           examcount=0;
                       }
                   }
                   if(y==16)
                   {
                       Right_Up_Point_finish_flag=0;
                       break;
                   }
                   if(y == 1)
                   {
                       break;
                   }
               }
            }
        }
        if(Left_Up_Point_finish_flag == 0)
        {
            if(y > Endline && Left_Black_Point[y+1]==0 && Left_Black_Point[y+2]==0 && Left_Black_Point[y+3]==0)     //左上拐点
            {
                star=y;
                for(uint8 y=star;y>=(star-22);y--)
                {
                    if(Left_Black_Point[y]>8 && Emo_abs(Left_Black_Point[y-1]-Left_Black_Point[y])<4
                   && Emo_abs(Left_Black_Point[y-2]-Left_Black_Point[y])<4 && Emo_imag[y][Left_Black_Point[y]+6] == EmoWhite
                   && Emo_imag[y-1][Left_Black_Point[y-1]+5] == EmoWhite && Emo_imag[y-2][Left_Black_Point[y]+5] == EmoWhite
                   && Emo_imag[y-3][Left_Black_Point[y]+5] == EmoWhite && Left_Black_Point[y] < Middle_Black_Point[y] && Emo_imag[y+3][Left_Black_Point[y]] == EmoWhite
                   && Emo_imag[y+5][Left_Black_Point[y]] == EmoWhite && Emo_imag[y+7][Left_Black_Point[y]] == EmoWhite)
                    {
                        findl_x=Left_Black_Point[y];
                        findl_y=y;
                        for(uint8 dircount = 0;dircount<5;dircount++)
                        {
                            examl_x=findl_x+directionlu[dircount][0];
                            examl_y=findl_y+directionlu[dircount][1];
                            if(Emo_imag[examl_y][examl_x]==255)
                            {
                                examcount++;
                            }
                        }
                        if(examcount>=4 && findl_y > Endline)
                        {
                            examcount=0;
                            Left_Up_Point[0]=findl_x;
                            Left_Up_Point[1]=findl_y;
                            if(Last_Left_Point[1] == 0)
                            {
                                Last_Left_Point[1] = Left_Up_Point[1];
                            }
                            if(Left_Up_Point[1] < 16)
                            {
                                Left_Up_Point[1] = Last_Left_Point[1];
                                Left_Up_Point_finish_flag = 0;
                            }
                            else
                            {
                                Left_Up_Point_finish_flag = 1;
                                Last_Left_Point[1] = Left_Up_Point[1];
                            }
                            findlcount=(int)star-(int)y;
                            break;
                        }
                        else
                        {
                            Left_Up_Point_finish_flag = 0;
                            examcount=0;
                        }
                    }
                    if(y==16)
                    {
                        Left_Up_Point_finish_flag=0;
                        break;
                    }
                    if(y == 1)
                    {
                        break;
                    }
                }
            }
        }
    }

}

圆环的类似拐点距离丢线行比较远，于是我选择放开上拐点的距离限制，转而记录下扫描的拐点距离丢线的行数，正好发现可以用来区分17届新加的元素P字 。

 当然因为如果距离圆环太远的话，圆环的特征是不太明显的，所以我会在识别到上下拐点时进入元素前摇的函数，在到达百分比区别P字和圆环前，将由此函数接管。

//元素前摇
//-------------------------------------------------------------------------------------------------------------------
//  @brief      元素前摇
//  @param
//  @param
//  @param
//  @param
//  @return     void
//  @note       在扫描到两个符合的上下两个拐点后，针对先形拐点进行判断是什么元素，判断包括圆环、十字、P字
//-------------------------------------------------------------------------------------------------------------------
void Windup(void)
{
    if(WindupL_flag == 1)
    {
        //Beepindex = Beepon;
        Link_Left_One_Point[0] = Left_Down_Point[0];
        Link_Left_One_Point[1] = Left_Down_Point[1];
        Link_Left_Two_Point[0] = Left_Up_Point[0];
        Link_Left_Two_Point[1] = Left_Up_Point[1];
        PaddingR = 0;
        PaddingL = 1;
        if(Right_Up_Point_finish_flag == 1 && Right_Down_Point_finish_flag == 1 && Left_Down_Point[1] > 42 && findlcount < 6 && Left_Up_Point[0] > 30)
        {
            Cross_flag = 1;
            WindupL_flag = 0;
            Beepindex = 0;
        }
        else if(Left_Up_Point_finish_flag == 1 && Left_Down_Point_finish_flag == 1 &&
                Right_Up_Point_finish_flag == 0 && Right_Down_Point_finish_flag == 0
                && Left_Down_Point[1] >= 75 && Left_Down_Point[1] <= 105 && findlcount < 4 && Left_Up_Point[0] > 30
                && (Left_Up_Point[0] - Left_Down_Point[0]) <= 42 && (Left_Down_Point[1] - Left_Up_Point[1]) >= 45
                && Right_Black_Point[Left_Up_Point[1]] < Right_Black_Point[(Left_Up_Point[1]+Left_Down_Point[1])/2]
                && Right_Black_Point[(Left_Up_Point[1]+Left_Down_Point[1])/2] <  Right_Black_Point[Left_Down_Point[1]]
                && Right_Black_Point[Left_Up_Point[1]] < Right_Black_Point[Emo_one_third(Left_Down_Point[1],Left_Up_Point[1])]
                && Right_Black_Point[Emo_one_third(Left_Down_Point[1],Left_Up_Point[1])] <  Right_Black_Point[Left_Down_Point[1]]
                && Right_Black_Point[Left_Up_Point[1]] < Right_Black_Point[Emo_two_third(Left_Down_Point[1],Left_Up_Point[1])]
                && Right_Black_Point[Emo_two_third(Left_Down_Point[1],Left_Up_Point[1])] <  Right_Black_Point[Left_Down_Point[1]]
                && Right_Black_Point[Left_Up_Point[1]] < Right_Black_Point[Left_Down_Point[1]])
        {
            SlalomLeft_flag = 1;
            Slalomcount = 1;
            WindupL_flag = 0;
        }
        else if(Left_Up_Point_finish_flag == 1 && Left_Down_Point_finish_flag == 1 &&
                Right_Up_Point_finish_flag == 0 && Right_Down_Point_finish_flag == 0
                && Left_Down_Point[1] >= 75 && findlcount >= 8 && Left_Up_Point[0] > 30 && (Left_Down_Point[1] - Left_Up_Point[1]) >= 45
                && (Left_Down_Point[1] - Left_Up_Point[1]) <= 78 && Emo_imag[Left_Up_Point[1]][Left_Up_Point[0] - 5] != EmoWhite
                && Right_Black_Point[Left_Up_Point[1]] < Right_Black_Point[(Left_Up_Point[1]+Left_Down_Point[1])/2]
                && Right_Black_Point[(Left_Up_Point[1]+Left_Down_Point[1])/2] <  Right_Black_Point[Left_Down_Point[1]]
                && Right_Black_Point[Left_Up_Point[1]] < Right_Black_Point[Emo_one_third(Left_Down_Point[1],Left_Up_Point[1])]
                && Right_Black_Point[Emo_one_third(Left_Down_Point[1],Left_Up_Point[1])] <  Right_Black_Point[Left_Down_Point[1]]
                && Right_Black_Point[Left_Up_Point[1]] < Right_Black_Point[Emo_two_third(Left_Down_Point[1],Left_Up_Point[1])]
                && Right_Black_Point[Emo_two_third(Left_Down_Point[1],Left_Up_Point[1])] <  Right_Black_Point[Left_Down_Point[1]]
                && Right_Black_Point[Left_Up_Point[1]] < Right_Black_Point[Left_Down_Point[1]])
        {
            if(findlcount >= 16)
            {
                CircleBig = 1;
            }
            CircleLeft_flag = 1;
            Circlecount = 1;
            WindupL_flag = 0;
        }
        else if(Left_Up_Point_finish_flag == 1 && Left_Down_Point_finish_flag == 1 && Right_Up_Point_finish_flag == 0 && Right_Down_Point_finish_flag == 0 && Left_Down_Point[1] <= 110
                && findlcount <= 17)
        {
            GarageL_Find();
            if(GarageL_Findfinish_flag == 1)
            {
                GarageL_Findfinish_flag = 0;
                GarageL_flag = 1;
                WindupL_flag = 0;
            }
        }
        else if(Left_Down_Point_finish_flag == 0)
        {
            WindupL_flag = 0;
            PaddingR = 0;
            PaddingL = 0;
            Beepindex = 0;
        }
    }
    else if(WindupR_flag == 1)
    {
        //Beepindex = Beepon;
        Link_Right_One_Point[0] = Right_Down_Point[0];
        Link_Right_One_Point[1] = Right_Down_Point[1];
        Link_Right_Two_Point[0] = Right_Up_Point[0];
        Link_Right_Two_Point[1] = Right_Up_Point[1];
        PaddingR = 1;
        PaddingL = 0;
        if(Left_Up_Point_finish_flag == 1 && Left_Down_Point_finish_flag == 1 && Right_Down_Point[1] > 42 && findrcount < 6 && Right_Up_Point[0] < 158)
        {
            Cross_flag = 1;
            WindupR_flag = 0;
            Beepindex = 0;
        }
        else if(Right_Up_Point_finish_flag == 1 && Right_Down_Point_finish_flag == 1 &&
                Left_Up_Point_finish_flag == 0 && Left_Down_Point_finish_flag == 0
            && Right_Down_Point[1] >= 75 && Right_Down_Point[1] <= 105 && findrcount < 4 && Right_Up_Point[0] < 158
            && (Right_Down_Point[0] - Right_Up_Point[0]) <= 42 && Right_Down_Point[1] - Right_Up_Point[1] >= 45
            && Right_Down_Point[1] - Right_Up_Point[1] <= 78 && Emo_imag[Right_Up_Point[1]][Right_Up_Point[0] + 5] != EmoWhite
            && Left_Black_Point[Right_Up_Point[1]] > Left_Black_Point[(Right_Up_Point[1]+Right_Down_Point[1])/2]
            && Left_Black_Point[(Right_Up_Point[1]+Right_Down_Point[1])/2] >  Left_Black_Point[Right_Down_Point[1]]
            && Left_Black_Point[Right_Up_Point[1]] > Left_Black_Point[Emo_one_third(Right_Down_Point[1],Right_Up_Point[1])]
            && Left_Black_Point[Emo_one_third(Right_Down_Point[1],Right_Up_Point[1])] >  Left_Black_Point[Right_Down_Point[1]]
            && Left_Black_Point[Right_Up_Point[1]] > Left_Black_Point[Emo_two_third(Right_Down_Point[1],Right_Up_Point[1])]
            && Left_Black_Point[Emo_two_third(Right_Down_Point[1],Right_Up_Point[1])] >  Left_Black_Point[Right_Down_Point[1]]
            && Left_Black_Point[Right_Up_Point[1]] > Left_Black_Point[Right_Down_Point[1]])
        {
            SlalomRight_flag = 1;
            Slalomcount = 1;
            WindupR_flag = 0;
        }
        else if(Right_Up_Point_finish_flag == 1 && Right_Down_Point_finish_flag == 1 &&
                Left_Up_Point_finish_flag == 0 && Left_Down_Point_finish_flag == 0
            && Right_Down_Point[1] >= 75 && findrcount >= 9 && Right_Up_Point[0] < 158 && Right_Down_Point[1] - Right_Up_Point[1] >= 45
            && Left_Black_Point[Right_Up_Point[1]] > Left_Black_Point[(Right_Up_Point[1]+Right_Down_Point[1])/2]
            && Left_Black_Point[(Right_Up_Point[1]+Right_Down_Point[1])/2] >  Left_Black_Point[Right_Down_Point[1]]
            && Left_Black_Point[Right_Up_Point[1]] > Left_Black_Point[Emo_one_third(Right_Down_Point[1],Right_Up_Point[1])]
            && Left_Black_Point[Emo_one_third(Right_Down_Point[1],Right_Up_Point[1])] >  Left_Black_Point[Right_Down_Point[1]]
            && Left_Black_Point[Right_Up_Point[1]] > Left_Black_Point[Emo_two_third(Right_Down_Point[1],Right_Up_Point[1])]
            && Left_Black_Point[Emo_two_third(Right_Down_Point[1],Right_Up_Point[1])] >  Left_Black_Point[Right_Down_Point[1]]
            && Left_Black_Point[Right_Up_Point[1]] > Left_Black_Point[Right_Down_Point[1]])
        {
            if(findrcount >= 16)
            {
                CircleBig = 1;
            }
            CircleRight_flag = 1;
            Circlecount = 1;
            WindupR_flag = 0;
        }
        else if(Right_Up_Point_finish_flag == 1 && Right_Down_Point_finish_flag == 1 &&
                Left_Up_Point_finish_flag == 0 && Left_Down_Point_finish_flag == 0 && Right_Down_Point[1] <= 110 && findrcount <= 17)
        {
            GarageR_Find();
            if(GarageR_Findfinish_flag == 1)
            {
                GarageR_Findfinish_flag = 0;
                GarageR_flag = 1;
                WindupR_flag = 0;
            }
        }
        else if(Right_Down_Point_finish_flag == 0)
        {
            WindupR_flag = 0;
            PaddingR = 0;
            PaddingL = 0;
            Beepindex = 0;
        }
    }
}

因为上下拐点之间是有丢线的，所以我们需要做补线处理。

补线

对于十字或者刚开始的P字和圆环，我们只要补直线就好。

/*******************补线**********************/
//先找到要补充的两条线，通过两点计算斜率得到两点组成的一次方程，得到剩余x的位置，将线换做左右边线
//-------------------------------------------------------------------------------------------------------------------
//  @brief      直线补线函数
//  @param      xone  第一个补线点x坐标
//  @param      yone  第一个补线点y坐标
//  @param      xtwo  第二个补线点x坐标
//  @param      ytwo  第二个补线点y坐标
//  @return     void
//  @note  Left_Black_Point[y]为我的左边线数组 Right_Black_Point[y]为我的右边线数组
//-------------------------------------------------------------------------------------------------------------------
void Padding_LineR(uint8 xone,uint8 yone,uint8 xtwo,uint8 ytwo)
{
    float k=0;  //斜率
    float b=0;  //截距
    //uint8 xstar=0;
    //uint8 xend=0;
    uint8 ystar=0;
    uint8 yend=0;

    k=((float)ytwo - (float)yone)/((float)xtwo - (float)xone);
    //k=((float)xtwo - (float)xone)/((float)ytwo - (float)yone);
    b=(float)yone - ((float)xone*k);

    if(yone>ytwo)
    {
        ystar=ytwo;
        yend=yone;
    }
    else
    {
        ystar=yone;
        yend=ytwo;
    }
    for(uint8 y=ystar;y<=yend;y++)
    {
        Right_Black_Point[y]=(uint8)(((float)y-b)/k);  //两点之间补线
    }
}

而对于入环和出环这类的控制，我们希望车子运行能够更加顺滑一些，于是我们选择补曲线。当然还需注意开始和结束补线的时机。

//补曲线，利用弯道进行补
//Cx曲线上点x，Cy曲线上点y
//-------------------------------------------------------------------------------------------------------------------
//  @brief      曲线补线函数
//  @param      Ux  上补线点x坐标
//  @param      Uy  上补线点y坐标
//  @param      Dx  下补线点x坐标
//  @param      Dx  下补线点y坐标
//  @return     void
//  @note       利用拉个朗日插值法，上下两个点由图像决定，中间点为固定点，如果补线效果不好，需要重新校准中间点
//  Left_Black_Point[y]为我的左边线数组 Right_Black_Point[y]为我的右边线数组
//-------------------------------------------------------------------------------------------------------------------
void Padding_CurveL(uint8 Ux,uint8 Uy,uint8 Dx,uint8 Dy)
{
    int x0 = 0,x1 = 0,x2 = 0;
    int y0 = 0,y1 = 0,y2 = 0;


    //0.0096   -2.1047  138.5182
    //0.0103   -2.2049  141.8985
    //x=x0(y-y1)(y-y2)/(y0-y1)(y0-y2)+x1(y-y0)(y-y2)/(y1-y0)(y1-y2)+x2(y-y0)(y-y1)/(y2-y0)(y2-y1)
    x0 = (int)Dx;
    x1 = (int)(Dx + (float)3*(Ux-Dx)/5);
    x2 = (int)Ux;
    y0 = (int)Dy;
    y1 = (int)(Dy - (float)2*(Dy-Uy)/3);
    y2 = (int)Uy;
    if(Ux == 0 && Ux == 0 && Dx == 0 && Dy == 0)
    {

    }
    else
    {
        if(Dy > 110)
        {
            Dy = 110;
        }
        //Re = Left_Black_Point[Dy];
//        Left_Black_Point[Dy] = (uint8)(a*(float)(Dy*Dy)+b*(float)Dy+c);
        //error = (int)Re - (int)Left_Black_Point[Dy];
        for(uint8 y = Uy ;y <= Dy;y++)
        {
//            Re = y - Uy + 25;
//            Left_Black_Point[y]=(uint8)(a*(float)(Re*Re)+b*(float)Re+c);
            Left_Black_Point[y]=(uint8)((x0*(y-y1)*(y-y2))/((y0-y1)*(y0-y2)))+((x1*(y-y0)*(y-y2))/((y1-y0)*(y1-y2)))+((x2*(y-y0)*(y-y1))/((y2-y0)*(y2-y1)));
        }
    }

}

void Padding_CurveR(uint8 Ux,uint8 Uy,uint8 Dx,uint8 Dy)
{
    int x0 = 0,x1 = 0,x2 = 0;
    int y0 = 0,y1 = 0,y2 = 0;
    //0.0096   -2.1047  138.5182
    //0.0103   -2.2049  141.8985
    //x=x0(y-y1)(y-y2)/(y0-y1)(y0-y2)+x1(y-y0)(y-y2)/(y1-y0)(y1-y2)+x2(y-y0)(y-y1)/(y2-y0)(y2-y1)
    x0 = (int)Dx;
    x1 = (int)(Dx - (float)3*(Dx-Ux)/5);
    x2 = (int)Ux;
    y0 = (int)Dy;
    y1 = (int)(Dy - (float)2*(Dy-Uy)/3);
    y2 = (int)Uy;
    if(Ux == 0 && Ux == 0 && Dx == 0 && Dy == 0)
    {

    }
    else
    {
        if(Dy > 110)
        {
            Dy = 110;
        }
        for(uint8 y = Uy ;y <= Dy;y++)
        {
            Right_Black_Point[y]=(uint8)((x0*(y-y1)*(y-y2))/((y0-y1)*(y0-y2)))+((x1*(y-y0)*(y-y2))/((y1-y0)*(y1-y2)))+((x2*(y-y0)*(y-y1))/((y2-y0)*(y2-y1)));
        }
    }

}

 

 补线的点的确定就需要同学自己去定了，也可以参考我的源码上边的点。为了不让元素的代码很乱，所以我选择在需要补线的地方选定补线的点，并打开补线标志，这样当独列出一个函数用来补线，就不会造成元素的代码里边充斥着补线的代码。不然更改补线方式后，需要对每个补线的程序进行更改。

//-------------------------------------------------------------------------------------------------------------------
//  @brief      补线函数
//  @param      PaddingR  右补线标志  0：不补线 1：要补线
//  @param      PaddingL  左补线标志
//  @param      Padding_CurveR  右曲线补线标志 0：补直线 1：补曲线
//  @param      Padding_CurveL  左曲线补线标志
//  @return     void
//  @note       补线的方式都通过此函数进行，外部只需要做到决定补线点的位置，和是否左右补线
//  Left_Black_Point[y]为我的左边线数组 Right_Black_Point[y]为我的右边线数组
//-------------------------------------------------------------------------------------------------------------------
void Padding_Line(void)
{
    if(PaddingL == 1 && PaddingR == 1 && Paddingcurve == 0)
    {
        Padding_LineR(Link_Right_One_Point[0],Link_Right_One_Point[1],Link_Right_Two_Point[0],Link_Right_Two_Point[1]);
        Padding_LineL(Link_Left_One_Point[0],Link_Left_One_Point[1],Link_Left_Two_Point[0],Link_Left_Two_Point[1]);
    }
    else if(PaddingL == 1 && PaddingR == 0 && Paddingcurve == 0)
    {
        Padding_LineL(Link_Left_One_Point[0],Link_Left_One_Point[1],Link_Left_Two_Point[0],Link_Left_Two_Point[1]);
        Padding_LineR(0,0,0,0);
    }
    else if(PaddingL == 0 && PaddingR == 1 && Paddingcurve == 0)
    {
        Padding_LineR(Link_Right_One_Point[0],Link_Right_One_Point[1],Link_Right_Two_Point[0],Link_Right_Two_Point[1]);
        Padding_LineL(0,0,0,0);
    }
    else if(PaddingL == 0 && PaddingR == 1 && Paddingcurve == 1)
    {
        Padding_CurveR(Link_Right_One_Point[0],Link_Right_One_Point[1],Link_Right_Two_Point[0],Link_Right_Two_Point[1]);
        Padding_CurveL(0,0,0,0);
    }
    else if(PaddingL == 1 && PaddingR == 0 && Paddingcurve == 1)
    {
        Padding_CurveL(Link_Left_One_Point[0],Link_Left_One_Point[1],Link_Left_Two_Point[0],Link_Left_Two_Point[1]);
        Padding_CurveR(0,0,0,0);
    }
    else
    {
        Padding_LineL(0,0,0,0);
        Padding_LineR(0,0,0,0);
    }
}

 最后

如果有对本文章有建议或者看法的话，可以评论或者私信我，希望可以和各位多多交流。本文章中的代码已经开源，开源地址：GitHub - StingeMoZGD/17th-SmartCar: 17届智能车竞赛，无线充电组