低信噪比信号相干积累matlab,一种基于下采样-串行FFT的高动态低信噪比信号粗捕获方法与流程...
本发明属于信号检测与估计技术领域,涉及一种能够在较大多普勒频偏和低信噪比环境下完成突发信号的检测方法。具体为一种基于下采样和fft结合的低复杂度信号检测算法。
背景技术:
突发通信是数字通信中的重要应用场景,在移动通信、应急通信以及卫星通信等领域都有着广泛的应用。而这些领域的很多应用环境通常又都具有高动态、低信噪比的特点,因此完成高动态、低信噪比环境下的信号检测是确保突发通信能够正常应用的前提。在高动态、低信噪比环境下进行突发通信,既要估计信号的到达时间,也要估计信号的频率,因此需要对信号进行时频二维搜索。理论上,对信号进行时频二维搜索的最大似然检测(ml)方法是在滑动地计算接收信号的周期图,即每滑动一个信号码片就通过快速傅里叶变换(fft)搜索其功率谱的最大值点,并与门限值进行比较和判决。这种方法的抗噪声和抗频偏性能都是最佳的,但是由于其计算复杂度过高,给实际实现带来了极大的困难,故而通常不会被采用。目前而言,在实际实现中较为常见的时频二维搜索算法是基于部分匹配滤波(pmf)的系列算法,例如pmf非相干叠加、pmf差分相干叠加以及pmf-fft算法。前两种算法仅能检测到信号的存在性,并不能估计其频率,而pmf-fft算法既能够完成信号的检测也能够完成频率的估计,因此在实际实现中最为常用。该算法的基本思想是,在滑动地检测到达信号时,首先对信号进行分段,并对每一段信号进行段内求和(或称段内相干积分),此时信号的点数将明显下降,此时再通过fft计算信号的功率谱并搜索其最大值点进行门限判决。尽管pmf-fft算法并非最优,但其明显地降低了计算复杂度,同时还能保证较好的抗噪声和抗频偏性能,实现了性能和算法复杂度上比较好的折衷,是一种优秀的时频二维搜索算法。
pmf-fft的缺陷在于,算法的抗频偏性能与分段的数目密切相关:如果想要较大的频率检测范围,则需要将每一段的数据量减少,或者分段的段数增大;但如果想要降低计算量,就需要分段的数目尽可能小,不论如何,此算法的频率检测范围由于分段的影响相比于直接进行周期图检测都要小得多。除此之外,算法的抗噪声性能与信号的频偏具有相关性,信号的多普勒频偏越大,pmf-fft得到的频谱最大值点幅度将越小,也就是说峰值信噪比(psnr)越低,显然这将使得检测性能变差。与pmf有关的其它算法都有类似的缺点,因此此处不再赘述。
技术实现要素:
本发明针对背景技术的缺陷,提出了一种基于直接差分相干积累的直扩信号捕获方法,用以完成大频偏下直扩信号的同步粗捕获。
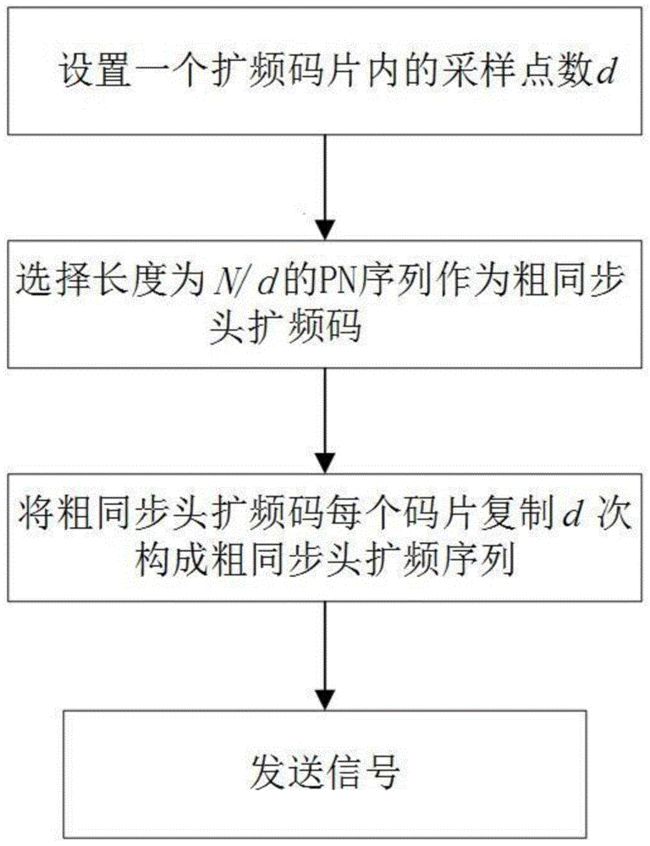
首先定义本发明需要的同步头序列帧格式。设所需的同步头长度为n,下采样率为d,在后面的算法描述中将指出,每接收到一个码片时,仅对n/d点序列进行处理。那么选取长度为n/d的pn序列c=[c(0),c(1),...,c(n/d-1)]t,将c的每个元素都复制扩展d倍,由此得到所需的同步头s,即:
本发明提出一种逐时刻进行小点数fft,并联合多个连续时刻的fft结果检测信号和估计信号频率的算法。具体而言,本发明算法将信号的检测和频率的估计分成两个阶段进行,仅当检测到信号时才会启动频率的估计。在信号检测阶段,滑动地接收信号序列,并始终存储长度等于n所使用同步头长度的序列r,每个采样时刻滑动接收一个码片,使用特定的下采样率d对序列进行下采样,并对得到的n/d点序列进行fft,设当前时刻为n,得到的fft序列为yn,则将当前时刻得到的yn与之前n-d+1个时刻得到的fft序列平方求和(非相干叠加)得到zn,即:
检测步骤的最后,找到序列zn的最大值及峰值的位置p,将同预先设定的门限t进行比较,当多个时刻的超过门限时,说明检测到信号,此时继续计算直到低于门限值的时候,取出从输出同步时刻ns以及峰值位置p,启动频率估计模块,否则继续搜索。在频率估计阶段,根据信号检测得到的同步时刻ns得到序列:
yf=[yn-d+1(p),yn-d+2(p),...,yn(p)]t
针对峰值位置p得到相位补偿序列dp=[1,ej2πp·1/n,...,ej2πp·(d-1)/n]t。计算yf经过相位补偿后的序列y′f,即
y′f(i)=yf(i)dp(i),i-0,1,...,d-1
得到y′f的fft结果y′f,找到序列y′f的最大值位置q后,即可按照以下公式估计信号频率:
其中fs为接收机的采样频率。一般设fs为码片周期的倒数。
本发明详细的实施方案为一种基于下采样-串行fft的高动态低信噪比信号粗捕获方法,该方法包括以下步骤:
步骤1、接收机以采样率fs采样以接收离散信号序列,设当前时刻为n,则始终保持一个由当前得到的采样点r(n)以及之前n-n+1个时刻的采样点组成的序列r,即使r类似于一个长度为n的队列,每收到一个采样点就将其压入r最前端,并且将其最末端的采样点删除,转入步骤2;
步骤2、以下采样率d对r进行抽取,得到长度为n/d的序列,对此序列进行fft得到yn,转入步骤3;
步骤3、如果n>d-1,将当前时刻得到的yn与之前n-d+1个时刻得到的fft序列平方求和得到zn,即:
其中yi(j)表示yn中的第j个元素,zn(j)表示zn中的第j个元素,转入步骤4;如果n<d-1,则返回步骤2;
步骤4、设置合适的门限t以及常数c,找到序列zn中元素的最大值将其与门限t进行比较,转入步骤5;
步骤5、如果当前时刻以及之前连续c-1个时刻的zn峰值均大于t,则说明检测到信号,记下第一次检测到信号的时刻na;继续执行步骤1~4进行检测,直到出现zn小于门限值时停止,记下停止时刻为nb,转入步骤6;
步骤6、根据na和nb生成峰值序列找到序列中的最大值,假设最大值在序列中的位置为nc,则可以计算出精确的同步位置为:
ns=na+nc-c+1
至此,捕获环节完成,转入步骤7进行频率估计;
步骤7、根据信号检测得到的同步时刻ns找到中元素的最大值位置p;生成序列:
以及相应的相位补偿向量dp=[1,ej2πp·1/n,...,ej2πp·(d-1)/n]t,对yf进行相位补偿得到y′f:
y′f(i)=yf(i)dp(i),i-0,1,...,d-1
计算y′f的fft序列y′f,找到序列y′f的最大值位置q后,按照以下公式估计信号频率:
本发明的主要特点在于:第一、通过特别设计的粗同步头,使得对整段长度为n的序列进行fft的运算可以均摊到不同时刻进行,由此,每次进行的fft点数大为减少,相比于直接进行周期图计算的方法,单位时间内的计算量得到了显著降低,而与pmf-fft相比,计算复杂度并无明显提升;第二、与门限进行比较的变量是多个时刻序列相同位置非相干叠加的结果,这就消除了相位的影响,使得峰值不会受到频偏的影响,即psnr不会随着频偏而产生明显的变化,这就扩展了频率搜索的范围;第三、尽管以下采样率d对信号进行下采将造成频谱的混叠,但步骤7解决了这个问题,使得频率搜索扩大到与直接计算周期图一样的范围大小。综上,在相同参数设置下(下采样率d等于pmf的长度,序列的总长度相同)本发明同pmf-fft一样,在每个时刻仅需计算点数为n/d的fft,因此计算复杂度与pmf-fft大致相同,但本发明的频率搜索范围却明显大于pmf-fft算法。值得注意的是,因为需要存下多个时刻的fft数据,因此本发明所需的存储空间将比pmf-fft要大。除此之外,由于与门限进行对比的峰值变量是非相干叠加的结果,因此在频偏较低的情况下本发明的psnr会低于pmf-fft算法,也就是说频偏较小时,pmf-fft的抗噪声性能将强于本发明。
附图说明
图1为本发明在发端的同步头构造流程图。
图2为本发明在收端的处理流程图。
图3为本发明方法与背景技术中pmf-fft算法在不同信噪比,频偏等于零条件下的捕获概率性能对比图。
图4为背景技术中pmf-fft算法在信噪比-18db,不同频偏条件下的捕获概率性能图。
图5为本发明方法在信噪比-18db,不同频偏条件下的捕获概率性能图。
具体实施方式
下面结合附图和实施例,详述本发明的技术方案。但不应将此理解为本发明上述主体的范围仅限于以下实施例,凡基于本发明内容所实现的技术均属于本发明的范围。
图1所示是本发明的一个具体实施例的发端的必要参数初始化的流程图。
包括以下步骤:
步骤1、设置同步头的长度为n=8192,下采样率为d=64。
步骤2、选择长度为64的m序列作为pn码c。
步骤3、将c中每个码片的码片周期由1扩展到d,生成同步头s。
图2所示是本发明基于图1的具体实施例的收端处理系统框图。
包括以下步骤:
步骤1、设当前时刻为n,则当前存储的由当前得到的采样点r(n)以及之前n-n+1个时刻的采样点组成的序列r为:
r=[r(n-8191),r(n-8190),...,r(n)]t
转入步骤2。
步骤2、以下采样率d对r进行抽取,得到序列:
rd=[r(n-8128),r(n-8064),...,r(n)]t
对rd进行fft,得到yn,转入步骤3。
步骤3、如果n>63,将当前时刻得到的yn与之前n-63个时刻得到的fft序列非相干叠加得到zn,即:
转入步骤4;如果n<63,则返回步骤2。
步骤4、设置门限t=4nn0=32768n0以及常数c=4,其中n0为噪声方差。找到序列zn的最大值将其与门限t进行比较,转入步骤5。
步骤5、如果当前时刻以及之前连续3个时刻的zn峰值均大于t,则说明检测到信号,记下第一次检测到信号的时刻na。继续执行步骤1~4进行检测,直到出现zn小于门限值时停止,记下停止时刻为nb,转入步骤6。
步骤6、根据na和nb生成峰值序列找到序列中的最大值,假设最大值在序列中的位置为nc,则可以计算出精确的同步位置为:
ns=na+nc-3
转入步骤7。
步骤7、根据信号检测得到的同步时刻ns找到的最大值位置p。生成序列:
以及相应的相位补偿向量dp=[1,ej2πp·1/8192,...,ej2πp·63/8192]t,对yf进行相位补偿得到y′f:
y′f(i)=yf(i)dp(i),i-0,1,...,63
计算y′f的fft序列y′f。找到序列y′f的最大值位置q后,即可按照以下公式估计信号频率:
由此完成信号频率估计环节,算法结束。
利用matlab仿真软件对背景技术中的pmf-fft算法和本发明实施例的串行fft信号检测估计算法在信噪比为snr=-30:1:-15,频偏fd=0的环境下进行仿真对比分析,仿真结果图3所示。图3展示了本发明与pmf-fft算法的捕获性能差异。由图可知,本发明由于使用了非相干叠加得到的变量与门限进行比较的缘故,在低频偏下的psnr不如pmf-fft算法,导致捕获性能差了大约5db,这是消除相位影响所带来的代价。除此之外,在图4中还展示了信噪比snr=-21db,频偏fd=0:10:150(频点)下pmf-fft的捕获性能,在图5中展示了在snr=-21db,频偏fd=0:10:150(频点)下本发明的捕获性能。通过图4和图5进行对比可以发现pmf-fft的捕获性能随着频偏的增大而不断降低,而本发明的捕获性能却能够始终维持在接近或者等于100%的捕获概率。因此,在计算复杂度相差不大的情况下,本发明的抗噪性能略差于pmf-fft,而频率搜索范围远大于后者。