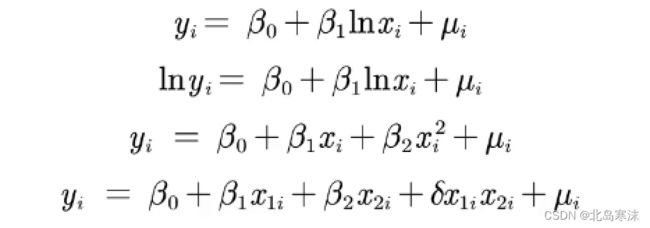数学建模学习笔记(9)多元线性回归分析(非常详细)
多元线性回归分析
-
- 1.回归分析的地位、任务和分类
- 2.数据的分类
- 3.对线性的理解、系数的解释和内生性
- 4.取对数预处理、虚拟变量和交互效应
- 5.使用Stata进行多元线性回归分析
- 6.异方差
- 7.多重共线性
- 8.逐步回归法
1.回归分析的地位、任务和分类
回归分析的地位:数据分析中最基础也是最重要的分析工作,绝大多数的数据分析问题都可以使用回归的思想来解决。
回归分析的任务:通过研究自变量和因变量的相关关系,尝试用自变量来解释因变量的形成机制,从而达到通过自变量去预测因变量的目的。具体如下:
- 判断哪些自变量和因变量是真的相关,而哪些自变量与因变量不相关。
- 判断与因变量相关的自变量的相关关系是正相关还是负相关。
- 对于不同的权重,称为回归系数,用于判断不同自变量对因变量的相对重要性。
备注:
①相关性和因果性的关系:相关性容易和因果性弄混淆。在绝大多数情况下,我们都没有能力去探究严格的因果关系,所以只能退而求其次研究相关关系。
②解释变量与被解释变量:自变量也称为解释变量;因变量也称为被解释变量。
③统一量纲的处理:根据回归系数比较不同自变量的相对重要性时首先需要统一量纲,进行标准化回归。
常见的回归分析类型:线性回归、0-1回归、定序回归、计数回归和生存回归。这些类型的划分依据是因变量的类型。
| 回归类型 | 因变量类型 | 求解模型 |
|---|---|---|
| 线性回归 | 连续数值型变量 | 普通最小二乘法(OLS)、广义最小二乘法(GLS) |
| 0-1回归 | 二值变量 | 逻辑斯蒂回归 |
| 定序回归 | 定序变量 | Probit回归 |
| 计数回归 | 计数变量 | 泊松回归 |
| 生存回归 | 定序变量 | Cox等比例风险回归 |
备注:生存变量是指经过截断后的寿命数据。
回归分析的数据要求:样本数要不少于自变量个数才能进行回归分析。
2.数据的分类
- 横截面数据:在某一个时间点收集的不同对象的数据。
- 时间序列数据:对同一对象在不同时间连续观察所取得的数据。
- 面板数据:将横截面数据和时间序列数据综合起来获得的一种数据资源结构。
建模比赛中常考的数据类型:建模比赛中最常用到的是横截面数据和时间序列数据;面板数据更加复杂,属于计量经济学中的模型内容。
不同数据类型的求解模型:横截面数据往往可以使用回归模型进行建模;时间序列数据往往需要我们进行预测,可选的模型较多
3.对线性的理解、系数的解释和内生性
一元回归模型和多元回归模型:只有一个自变量的回归模型称为一元回归模型,有多个自变量的回归模型称为多元回归模型。
回归模型与拟合模型的区别:
- 扰动项:线性回归模型中增加了一个扰动项,扰动项需要满足一定的条件。
- 残差:预测值和实际值之间的差值称为残差,线性回归模型想要得到残差平方和最小的模型。
对线性的理解:只要能够通过一定的转换将自变量和因变量转换成线性关系都可以认为是线性模型。因此下图中的四个表达式都可以认为是线性模型。
数据转换使用的软件:数据转换在数据预处理步骤完成,使用Excel、Matlab或Stata都可以对数据进行预处理。
回归系数的解释:
- 截距项可忽略:截距项的数值本身意义不大。
- 控制变量法:对于回归系数的解释注意需要控制变量。
内生性的相关概念:
- 内生性和外生性的定义:如果模型的扰动项与所有的自变量均不相关,则称该模型具有外生性;如果存在相关,则称存在内生性。
- 内生性带来的问题:内生性会导致回归系数估计不准确:不满足无偏性(期望值和真实值相等)和一致性(样本足够大时估计值依概率收敛于真实值)。
- 内生性的本质:模型扰动项中包含了所有与因变量相关,但是未添加到回归模型中的变量;如果这些变量和已经添加到模型中的自变量相关就会存在内生性。
控制模型内生性的方法:严格外生性的条件非常苛刻,因为解释变量一般非常多,因此实际使用时需要弱化条件,将解释变量分为核心解释变量和控制变量。
- 核心解释变量:最需要进行研究的变量,因此我们最希望能够得到其回归系数的一致性估计;
- 控制变量:本身不太需要研究,之所以将其放入模型中,主要是为了控制住那些对被解释变量有影响的遗漏因素。
在实际应用中,只需要保证核心解释变量与扰动项不相关即可。
4.取对数预处理、虚拟变量和交互效应
何时需要对变量取对数预处理:取对数意味着被解释变量对解释变量的弹性,也就是百分比的变化而不是数值的变化。取对数没有固定的规则,但是有一些经验法则。
- 与市场价值相关的变量可以取对数。
- 以年份进行度量变量通常不取对数。
- 用于表示比例的变量可以取对数也可以不取对数。
- 只有变量取值为非负数才能进行取对数,如果包含0则可以取对数ln(y+1)。
取对数的作用:
- 减弱数据的异方差性;
- 如果变量本身不符合正态分布,取对数后可能渐近服从正态分布,有利于进行假设检验;
- 使得模型更加具有经济学意义。
四类模型回归系数的解释:
- 一元线性回归模型(y=a+bx+u):x每增加一个单位,y平均变化b个单位;
- 双对数模型(lny=a+blnx+u):x每增加1%,y平均变化b%;
- 半对数模型(y=a+blnx):x每增加1%,y平均变化b/100个单位;
- 半对数模型(lny=a+bx):x每增加1%,y平均变化(100b)%。
虚拟变量:
- 何时引入:如果自变量中存在定性(类别)变量,就需要引入虚拟变量的概念。
- 解释与显著性:虚拟变量的解释仍然是类别之间的比较,同时还要关注显著性。
- 变量个数:为了避免完全多重共线性的影响,引入虚拟变量的个数一般是分类数-1。
自变量的交互效应:自变量的乘积作为一个新的自变量,表示因变量受到一个自变量和另一个自变量的共同影响。
5.使用Stata进行多元线性回归分析
Stata是进行多元线性回归分析最好用的软件之一。
Stata导入数据:文件→导入→Excel表格→确定。
Stata清空数据:使用clear命令。
Stata保存代码:新建一个do-file编辑器→在编辑器中输入代码→保存do文件。
Stata数据的描述性统计:
- 定量数据的描述性统计语法:
summarize 变量名1 变量名2....
定量数据的描述性统计结果: 定量数据的描述性统计结果中包含每一个变量对应的样本数、均值、标准差、最大值和最小值。
- 定性数据的描述性统计语法:
tabulate 变量名,gen(虚拟变量名)
定性数据的描述性统计:每次只能对一个定性变量进行描述性统计并生成指定名称的虚拟变量。描述性统计的结果是各个类别的频数和频率。
备注:
①频数饼状图的绘制:在得到某个定性数据的频数后,最好使用Excel绘制一张频数统计饼状图,这样使得得到的结果更加直观。
②总体描述性结果表格:在对所有变量都进行描述性统计后,最好绘制一张结果汇总分析表格,表格的样式可以如下图所示:
Stata进行回归分析:
- 回归分析语法:
regress 因变量 自变量1,自变量2... - 回归分析的求解算法:默认使用普通最小二乘估计法。
- 结果表格:需要关注的是表格中的拟合优度、调整后的拟合优度、联合显著性检验结果的P值、回归系数值、回归系数显著性的P值。
回归结果分析:
拟合优度的分析:
- 预测型回归才需要更关注拟合优度:回归可以分为用于因变量预测的预测型回归和用于分析因变量形成机制的解释型回归。预测型回归才会更加看重拟合优度;解释性回归更加关注模型整体的显著性以及自变量的统计显著性和经济意义显著性。
- 更关注调整后拟合优度:我们引入的自变量越多,拟合优度会变大。但是我们倾向于使用调整后的拟合优度,如果新引入的自变量对SSE的减小程度特别小,那么调整后的拟合优度反而会减小。
- 拟合优度较低的原因:数据中存在异常值或者数据本身分布不均匀都会使得拟合优度较低。
- 拟合优度较低的解决方法:如果拟合优度过低,可以尝试对数据取对数或者平方后再进行回归分析。
模型联合显著性:只有当对应的P值小于0.05才能认为该回归模型是显著的,才能够使用该模型。
回归系数表:回归系数表中记录了各个自变量对应的回归系数及它们对应的显著性检验P值,只有检验P值小于0.05的自变量才是显著的,需要进行分析。
Stata回归分析结果表格的docx保存:
首先需要再Stata中使用下列的命令安装第三方插件:ssc install reg2docx
在回归regress语句的下一条语句使用,首先保存模型结果:est store 模型名
最后将模型结果导出到一个文本文档中(docx):reg2docx 模型名 using docx文件名名,replace
标准化回归:
- 作用:通过对原始自变量数据进行标准化剔除各个自变量量纲的影响,用于评价不同自变量对因变量的相对重要程度。
- 比较方法:在系数显著的情况下,标准化系数的绝对值越大,表示对因变量的影响越大。
- 对系数显著性的影响:标准化回归不影响回归系数的显著性。
- Stata进行标准化回归语法:
regress 因变量 自变量1,自变量2... ,beta,标准化回归结果中会给出标准化回归系数, - 标准化回归模型没有常数项。
6.异方差
球型扰动项:之前讨论的多元线性回归模型中,我们都假设扰动项属于球型扰动项,也就是需要满足“同方差”和“无自相关”两个条件。但是实际问题中的扰动项不满足“同方差”性质,所以存在异方差问题;不满足“无自相关”性质,所以存在自相关问题。
- 横截面数据容易出现异方差问题;
- 时间序列数据容易出现自相关问题。
异方差带来的危害:
- 如果存在异方差,普通最小二乘法估计出来的回归系数仍然满足无偏性和一致性,但是由于构造的统计量失效因此无法使用假设检验,所以普通最小二乘法估计量不再是最优线性无偏估计量。
- 体现在回归结果上,就是回归系数表中很多回归系数都不显著。修复异方差问题后,回归系数表中将出现更多显著的回归系数。
异方差的检验:
1.残差图检验法:可以用Stata自带的残差图函数来直观检验异方差,但是可能不够准确。使用残差图检验之前需要首先进行回归分析。
残差图异方差检验语法:
rvfplot:作出残差和拟合值关系的散点图。如果拟合值较小时残差波动小,拟合值变大时残差波动也变大则可以判定存在异方差现象。rvpplot x:作出残差和自变量x关系的散点图。如果自变量很小时残差波动很大,自变量变大时残差波动减小,则说明存在异方差现象。
补充:
…
1.图像绘制完成的保存语法:graph export 保存文件名,replace
保存的文件和当前的Stata文件在同一个文件夹中。
其中的replace表示如果存在同名的图像,则进行替换。
…
2.绘制概率密度函数图的语法:kdensity 变量名
作用:用于判断某一个变量的值的分布情况。
…
3.获取某变量分布情况的统计表格:summarize 变量名,d
作用:可以求出在不同的百分数处对应的元素。
2.BP检验法:
- 检验语法:
estat hettest,rhs iid - 与怀特检验的关系:BP检验可以视为怀特检验的特例,一般使用怀特检验。
- 结果评判:只有检验P值大于等于0.05才认为不存在异方差。
3.怀特检验:
- 检验语法:
estat imtest,white - 结果评判:只有检验P值大于等于0.05才认为不存在异方差。
异方差问题的解决方法:
- 使用普通最小二乘法(OLS)+稳健标准误。
这是最简单也是目前最通用的方法,同时也是推荐在大多数情况下使用的方法。
Stata语法:regress 因变量 自变量1,自变量2... ,robust
- 使用广义最小二乘法(GLS)。
不推荐这种方法,因为由于我们不知道扰动项真实的协方差矩阵,因此只能通过样本数据来估计,这样得到的结果不稳健,存在偶然性。
7.多重共线性
多重共线性的概念:自变量之间存在较为严重的线性相关性。
完全多重共线性的相关概念:
- 完全多重共线性会导致回归系数无法计算出来,Stata可以自动识别并删除多余的解释变量来避免完全多重共线性的影响。
- 完全多重共线性在现实数据中很少出现。
多重共线性带来的问题:
- 回归系数估计不准确:多重共线性非常严重时,会导致回归系数估计不准确。
- 一般症状:回归模型的拟合优度很大,整体模型检验显著性也很高,但是单个回归系数的检验却不显著,或者系数估计值不合理甚至符号与理论预期相反。
多重共线性的检验:可以通过计算方差膨胀因子进行多重共线性检验。
- 每个自变量的VIF:对于每一个自变量都可以计算方差膨胀因子。VIF越大,说明该自变量与其他自变量的相关性越大。
- 整体模型的VIF:将模型中所有自变量的最大方差膨胀因子记作模型的方差膨胀因子VIF。一个经验规则是,如果模型的VIF>10,则认为该回归方程存在严重的多重共线性。
- Stata计算每个自变量的VIF语法:
estat vif(在回归分析后使用)
多重共线性的处理:
- 不关心回归系数的值可以不管多重共线性:在方程整体显著的情况下,如果不关心具体的回归系数,只关心方程对被解释变量的预测能力,则可以不用管多重共线性。这是因为,多重共线性的主要后果是对单个变量的贡献估计不准,但是所有变量的整体效应仍然可以较为准确地估计。
- 所关心变量的显著性不受影响则可以不管多重共线性:如果关心具体的回归系数,但是多重共线性并不影响所关心变量的显著性,那么也可以不必理会。因为消除多重共线性影响后这些回归系数只会更加显著。
- 多重共线性影响所关心变量的显著性:如果多重共线性影响到所关心变量的显著性,则需要增大样本容量,剔除导致严重多重共线性的变量(不要随意剔除,因为可能影响内生性)。
8.逐步回归法
逐步回归法的概述:逐步回归可以用于解决多重共线性问题。逐步回归可以分为向前逐步回归和向后逐步回归两种具体算法。
向前逐步回归法:
- 具体步骤:将自变量逐个引入模型,每引入一个自变量后都进行检验,只有该自变量显著时才加入模型中。
- 存在的问题:随着以后其他自变量的引入,原来显著的自变量也可能变得不显著了,但是并没有将其从回归模型中剔除掉。
- Stata语法:
stepwise regress y x1,x2... ,pe(显著性水平)
向后逐步回归法:
-
具体步骤:先把所有自变量放入模型,之后尝试将其中一个自变量从模型中剔除,看整个模型解释因变量的变异是否有显著变化,最后把最没用解释力的那个自变量剔除,直到没有自变量符合剔除的条件。
-
存在的问题:一开始把所有变量都引入回归方程,这样计算量非常大。不过,这个缺点随着计算机能力的提升已经不太影响了。因此更加推荐使用这种方法进行逐步回归。
-
Stata语法:
stepwise regress y,x1,x2... ,pr(显著性水平)
注意事项:
①避免完全多重共线性:Stata进行逐步回归时要求各个自变量之间不能存在完全多重共线性,这一点与使用Stata直接进行回归不同。
②显著性值会影响筛选的变量个数:显著性水平越高,筛选出的变量越多;显著性水平越低,筛选出的变量越少。
③向前逐步回归和向后逐步回归的结果可能不同。
④慎重使用逐步回归法。因为剔除了自变量后可能会产生新的如内生性问题。(数模比赛中也可以不考虑内生性)
⑤最好的变量筛选方法:如果可能,最好把每一种情况都尝试一次,如果不考虑效率的话这是最好的筛选方法。