#第25篇分享：一个用户签到位置数据挖掘实例（python语言：sklearn KNN）（1）

#sklearn-KNN算法，KNN算法一个不建模的算法，什么意思呢，就是不会提前生成模型，只要有数据输入后才会计算距离D，根据距离即可进行预测；朴素贝叶斯也是不建模算法，但是是用概率进行预测：

目的：预测用户签到位置；
工具：语言python；数据分析：pandas，matplotlib，numpy三剑客；数据预测：sklearn；
操作流程：查找并分析数据，sklearn KNN机器学习算法进行房价预测。

1.数据收集：kaggle上面的数据不太好下载，所以我把我找到的数据放在我的资源里面了，有需要可以自行下载：
数据位置：不需要积分，自行下载

2.KNN算法简介：（因为是遍历性质的计算，所以算法相对耗时；几千几万小数据用一用，看看效果，有时候效果还是很可观的）

a.算法概念:
K近邻是基于实例的分类(instance-based learning) ：比如在现实中，预测一个员工住的位置，就可以根据其他员工一些特征，及住宿位置（标签）：比如交通工具，出行时间，路过标志性建筑等等，通过计算预测员工与已知员工的欧氏距离d，预测员工大致位置。KNN没有明显的训练学习过程，不同K值的选择都会对KNN算法的结果造成重大影响。

K值的取值会影响预测的效果： 简单来说就是K太小，就是查找的范围变小了，也就是找到的样本变少，如果模型存在异常点，并且异常点距离预测值比较近，那么有可能我们预测结果就是错误的；
K值太大，我们查找范围变大，也就是查找样本增多，如果样本不均衡，内圈数据少，外圈数据多且分属于不同的类，那么我们的预测值就会跟外圈一致，出现错误预测；
对于K值的选取，我们可以用学习曲线进行观察，然后选出最合适的K值，但是KNN运算量很大，还是要根据实际情况进行操作。

b…算法思路（欧式距离d），当然还有其他距离，可以看下面的链接：
一个样本与数据集中的K个样本最相似，也就是距离d最接近， 如果这K个样本中的大多数属于某一个类别， 则该样本也属于这个类别；当然KNN也是可以做回归拟合的，但是机器学习算法很多，一般不会使用:KNN

c.优缺点：
优点： 理论成熟，思想简单；可用于线性及非线性分类；训练时间复杂度为O(n)；对数据没有假设，准确度高，对outlier（离群值）不敏感；
缺点：计算量大；样本不平衡问题（即有些类别的样本数量很多，而其它样本的数量很少）；需要大量的内存；

d.代码实例1（一个分类实例）：
预测用户签到的位置，这是一个之前的机器学习竞赛题目，网上资源也是很多：

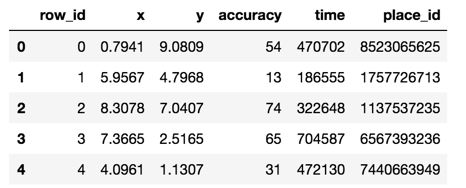
数据结构展示：

文件说明 train.csv, test.csv
  row id：签入事件的id
  x y：坐标
  accuracy: 准确度，定位精度
  time: 时间戳
  place_id: 签到的位置，这也是你需要预测的内容

下面代码注释已经写的很清楚了，我们不要着急看结果，一步一步的分析代码，学会思路才是不错的选择：

# coding=gb2312                    #加入编码格式
#=====K近邻算法==============根号（a1-a2）^2+(b1-b2)^2
'''
相似的样本特征都是相近的：就是找到距离最近的
K近邻算法要进行标准化。
'''
from sklearn.neighbors import KNeighborsClassifier    #KNN分类算法
import pandas as pd
from sklearn.model_selection import train_test_split  #分割测试集训练集
from sklearn.preprocessing import StandardScaler   #数据标准化
import matplotlib.pyplot as plt

'''
K-近邻预测用户签到位置：
'''
#1.读取数据：
data = pd.read_csv("./facebook-v-predicting-check-ins/train.csv")

#2.处理数据：
#缩小数据，查询数据信息：
data = data.query("x>1.0&x<1.25&y>2.5&y<2.75")

#处理时间数据：
time_value = pd.to_datetime(data["time"],unit="s")

#把日期转换为字典形式：
time_value = pd.DatetimeIndex(time_value)

#3.构造一些特征
data["day"] = time_value.day
data["hour"] = time_value.hour
data["weekday"] = time_value.weekday
data.drop(["time"],axis=1)

#把签到数量少于n个目标的位置删除：
place_count = data.groupby("place_id").count()
tf = place_count[place_count.row_id>3].reset_index()
data = data[data["place_id"].isin(tf.place_id)]

# print(data)
#取出数据当中的特征值和目标值
y = data["place_id"]
x = data.drop(["place_id"],axis=1)

#进行数据的分割训练集和测试集
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25)
#4.特征工程：标准化
std = StandardScaler()
#对测试集和训练集的特征值进行标准化：
x_train = std.fit_transform(x_train)
x_test = std.transform(x_test)

#5.模型训练：
score_1 = []
for i in range(1,30,5):
    knn = KNeighborsClassifier(n_neighbors=i)
    #fit,predict,score
    knn.fit(x_train,y_train)
    #6.结果预测：
    # y_predict = knn.predict(x_test)
    # print("预测目标的签到位置",y_predict)
    #得出准确率：
    # print("预测准确率：",knn.score(x_test,y_test))
    score_ = knn.score(x_test,y_test)
    score_1.append(score_)

#可视化寻找最佳K值：
import matplotlib
#设置中文字体能够显示：
font = {"family":"MicroSoft YaHei","weight":"bold","size":8}
matplotlib.rc("font",**font)

#绘制曲线：
plt.figure(figsize=(16, 10), dpi=144)
plt.plot(range(1,30,5), score_1, c='k', label='score_1', lw=4)  # 画出拟合曲线
plt.xticks(range(1,30,5))
plt.xlabel("K值")
plt.ylabel("模型评分：score_1")
plt.title("KNN-score_1")
plt.show()

我们看一下可视化的图片，准确率简直低的不行了，而且通过调节K值没有很大的改善，而可调参数只有K，标准化也做了，如果想提高分数，建议更换模型吧：

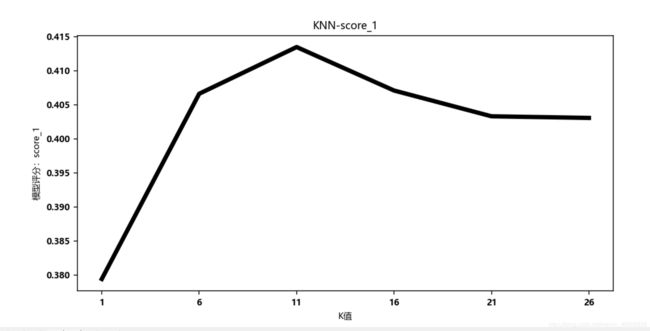
代码实例2（一个回归实例）：源码位置
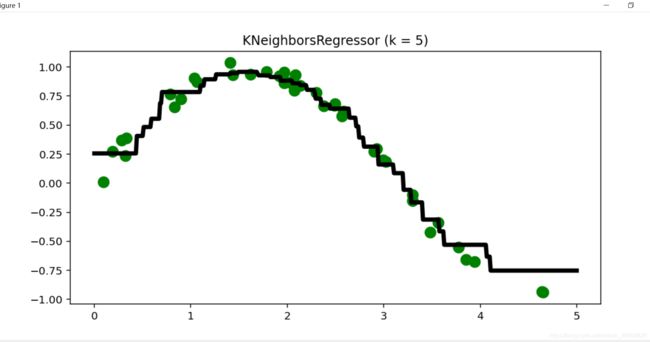
拟合一条sin曲线：

# coding=gb2312                    #加入编码格式
import matplotlib.pyplot as plt
import numpy as np

# 生成训练样本
n_dots = 40
#通过本函数可以返回一个或一组服从“0~1”均匀分布的随机样本值。随机样本取值范围是[0,1)，不包括1。 
X = 5 * np.random.rand(n_dots, 1)
#返回一个连续的扁平数组。
y = np.sin(X).ravel()

# 添加一些噪声到该数据中
y += 0.2 * np.random.rand(n_dots) - 0.1

#使用KNN算法进行回归拟合
from sklearn.neighbors import KNeighborsRegressor
#选取最近的5个样本决定这个事物属于哪类
k = 5
knn = KNeighborsRegressor(k)
#使用X作为训练数据并将y作为目标值来拟合模型
knn.fit(X, y);

# 生成足够密集的点并进行预测
#生成了一个一维500个数字的数组[:,np.newaxis]将数组转成500行1列的矩阵
T = np.linspace(0, 5, 500)[:, np.newaxis]
y_pred = knn.predict(T)
knn.score(X, y)

# 画出拟合曲线
#画图之前首先设置figure对象，此函数相当于设置一块自定义大小的画布，
# 使得后面的图形输出在这块规定了大小的画布上，其中参数figsize设置画布大小 dpi每英寸点数
plt.figure(figsize=(16, 10), dpi=144)
plt.scatter(X, y, c='g', label='data', s=100)         # 画出训练样本
plt.plot(T, y_pred, c='k', label='prediction', lw=4)  # 画出拟合曲线
plt.axis('tight')
plt.title("KNeighborsRegressor (k = %i)" % k)
plt.show()

有些事情还是不能想当然，我之前接触的时候真是没想到KNN还能做回归，一次偶然的机会突然看见了，感觉真的是非常的神奇，于是就写在这里了；之后我们还会遇见很多的算法，我也是从零了解到了很多，也是很感谢网上的视频资源，讲的真的是非常的好，现在这个时代，真的是只要你想学，资源遍地都是，我们在享受别人的成果的时候，也能思考着如何贡献自己的力量那就是极好的了，良性发展，共同进步。
持续更细，，，，，，