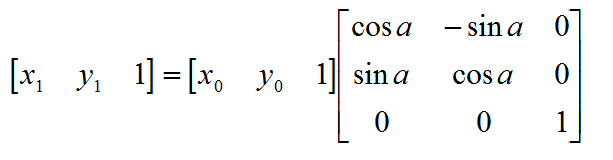python数字图像处理笔记10 图像旋转
图像旋转
def rotate(img, angle):
H, W, C = img.shape
anglePi = angle * math.pi / 180.0
cosA = math.cos(anglePi)
sinA = math.sin(anglePi)
out = np.zeros((H, W, C), dtype=np.uint8) # 必须是8 不然显示不出图像
for y in range(H):
for x in range(W):
x0 = int(x * cosA + y * sinA)
y0 = int(y * cosA - x * sinA)
if 0 < x0 < W and 0 < y0 < H: # 计算结果是这一范围内的x0,y0才是原始图像的坐标。
out[y0, x0] = img[y, x]
return out

旋转后的图像有很多“蜂窝煤”。主要是点转换后要取整。导致原图中有些点映射到同一个点,而生成的图中有些点在原图中没有点映射到它。所以出现了很多“蜂窝煤”。
以图像的中心进行旋转
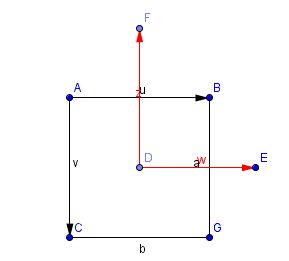
在矩阵中的坐标系通常是AB和AC方向的,而数学坐标系坐标系是DE和DF方向的。
令图像表示为M×N的矩阵,对于点A而言,两坐标系中的坐标分别是(0,0)和(-N/2,M/2)
矩阵中点(x’,y’)转换为笛卡尔坐标系(x,y)的转换关系为:

逆变换为
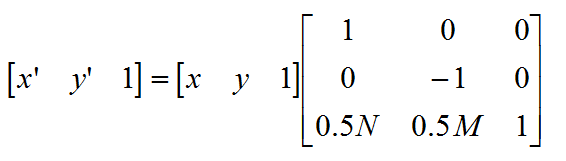
最后结果
1.首先将图像坐标系转换为数学坐标系。
2.使用旋转公式对坐标进行旋转。
3.将旋转后的数学坐标系转换为图像坐标系。
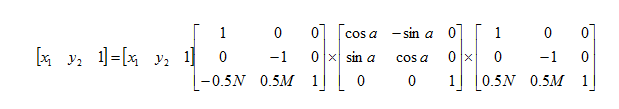
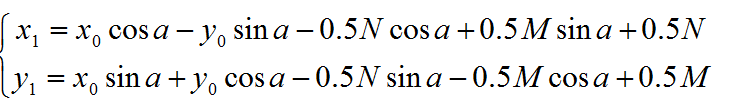
def rotate(img, angle):
H, W, C = img.shape
anglePi = angle * math.pi / 180.0
cosA = math.cos(anglePi)
sinA = math.sin(anglePi)
out = np.zeros((H, W, C), dtype=np.uint8) # 必须是8 不然显示不出图像
for y in range(H):
for x in range(W):
x0 = int(cosA * x - sinA * y - 0.5 * W * cosA + 0.5 * H * sinA + 0.5 * W)
y0 = int(sinA * x + cosA * y - 0.5 * W * sinA - 0.5 * H * cosA + 0.5 * H)
if 0 < x0 < W and 0 < y0 < H: # 计算结果是这一范围内的x0,y0才是原始图像的坐标。
out[y0, x0] = img[y, x]
return out
完整显示图片
图片旋转后图片可能变大

N’和M’对应于新图的宽和高
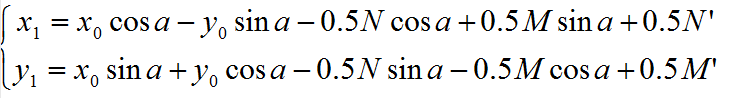
新图像的宽和高计算公式

def rotate(img, angle):
H, W, C = img.shape
anglePi = angle * math.pi / 180.0
cosA = math.cos(anglePi)
sinA = math.sin(anglePi)
# 三角函数计算出来的结果会有小数,所以做了向上取整的操作。
# size = (W + 1, H + 1)
new_height = math.ceil(H * cosA + W * sinA)
new_width = math.ceil(W * cosA + H * sinA)
out = np.zeros((new_height+1, new_width+1, C), dtype=np.uint8) # 必须是8 不然显示不出图像
for y in range(H):
for x in range(W):
x0 = int(cosA * x - sinA * y - 0.5 * W * cosA + 0.5 * H * sinA + 0.5 * new_width)
y0 = int(sinA * x + cosA * y - 0.5 * W * sinA - 0.5 * H * cosA + 0.5 * new_height)
# if 0 < x0 <= new_width and 0 < y0 <= new_height: # 计算结果是这一范围内的x0,y0才是原始图像的坐标。
out[y0, x0] = img[y, x]
return out
解决蜂窝煤
采用向后映射法,也可采用后向映射+双线性插值法
图像旋转的过程:1.将图像坐标转换为数学坐标。2.使用图像旋转的逆公式。3.将数学坐标转换为图像坐标。
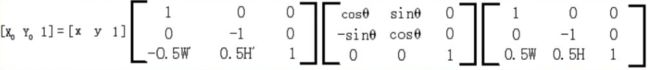
def rotate(img, angle):
H, W, C = img.shape
anglePi = angle * math.pi / 180.0
cosA = math.cos(anglePi)
sinA = math.sin(anglePi)
new_height = math.ceil(H * np.cos(anglePi) + W * np.sin(anglePi))
new_width = math.ceil(W * np.cos(anglePi) + H * np.sin(anglePi))
out = np.zeros((new_height+1, new_width+1, C), dtype=np.uint8) # 必须是8 不然显示不出图像
dx_back = 0.5 * W - 0.5 * new_width * cosA - 0.5 * new_height * sinA
dy_back = 0.5 * H + 0.5 * new_width * sinA - 0.5 * new_height * cosA
for y in range(new_height):
for x in range(new_width):
x0 =int( x * cosA + y * sinA + dx_back)
y0 = int(y * cosA - x * sinA + dy_back)
if 0 < x0 < W and 0 < y0 < H: # 计算结果是这一范围内的x0,y0才是原始图像的坐标。
out[y, x] = img[y0, x0] #。
return out

参考链接 https://www.cnblogs.com/xianglan/archive/2010/12/26/1917247.html
参考链接:https://www.cnblogs.com/liwill/p/13875745.html