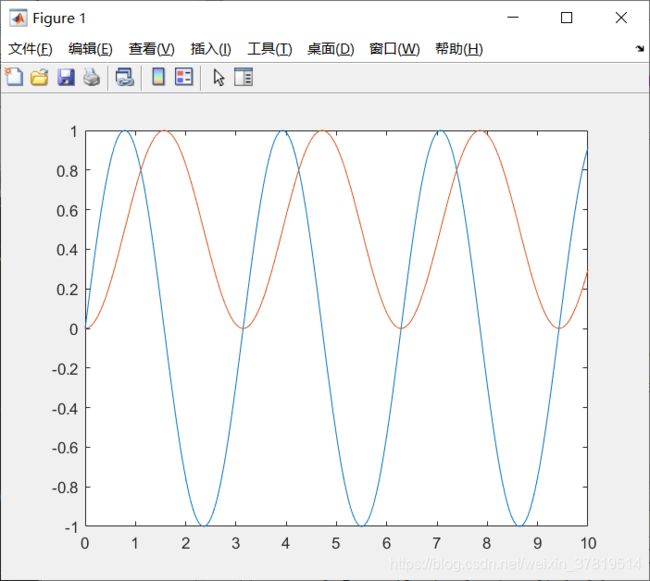
用一个简单的例子说明如何使用S函数进行Simulink建模
MATLAB中如何编写S-函数
- 前言
-
- 认识S函数模板
- 一个实际的栗子
- 仿真结果分析
-
- 参考资料
前言
在使用Simulink中搭建复杂的控制系统的时候,由于被控对象或者控制器较为复杂,仅仅使用Simulink中提供的常用模板无法实现简洁高效,这个时候就可以尝试编写S-Function函数,并将其封装为一个模块来使用。理论上,采用这种方法可以搭建出任何复杂的系统。本文将通过一个实例,来说明如何编写S函数,并用其搭建一个简单的Simulink模型。
认识S函数模板
S函数的编写可以在MATLAB提供的模板基础上直接完成。在MATLAB界面下的命令行窗口输入edit sfuntmpl,就能打开官方提供的S函数模板。使用时,只需要把这个.m文件另存为你需要的模块名称.m即可。
function [sys,x0,str,ts,simStateCompliance] = sfuntmpl(t,x,u,flag)
这个就是官方给出的文件开头第一行,说明了这个函数的输入及输出情况,官方代码中对此也有功能描述,再次不再赘述。我主要总结两点,一是sys是一个函数的返回值,在不同的函数(如:初始化、状态更新、输出函数中)中有不同的值,这个可理解为它不是一个变量,而是不同函数内部的返回值,但是使用了同一个关键字;二是x表示状态变量,u表示输入变量,他们是不一样的。学过现代控制理论的就可以知道,状态变量和输入变量是不一样的。也就是Dx/dt = AX+BU;Y = CX+DU,对于所有的函数关系都可以使用状态方程来描述,就是这个道理。
一个实际的栗子
假设有一个系统,如下所示
dx/dt = u;
y = x;
其中,u为输入,x为状态变量,y为输出。计算系统在零初始条件下,正弦信号sin(2t)输入下的输出。
这个问题比较简单,单纯手算也能很快计算出来,再次只是示意如何使用S-函数。
根据上面的描述,在同一个文件夹下面,建立一个.slx文件,这是simulink的模型文件;再将上面S-函数模板另存为一个自己的模板文件(注意函数名应该与.m文件名一致),修改这个模板文件,代码如下:
function [sys,x0,str,ts,simStateCompliance] = move(t,x,u,flag)
% sys:是一个通用的返回参数,它所返回值的意义取决于flag的值,sys输出根据flag的不同而不同
% x0:是初始的状态值(没有状态时是一个空矩阵[]),这个返回参数只在flag值为0时才有效,其他时候都会被忽略。
switch flag,
case 0,
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u); %flag=1表示此时要计算连续状态的微分
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case 4,
% flag=4表示此时要计算下一次采样的时间,只在离散采样系统中有用(即mdlInit ializeSizes中的ts设置ts(1)不为0)
% 连续系统中只需在mdlGetTimeOfNextVarHit函数中写上sys=[];这个函数主要用于变步长的设置
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 1;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1; % at least one sample time is needed
sys = simsizes(sizes);
x0 = [0]; % 状态变量初值为0
str = []; % 保留变量,赋值为[]
ts = [0 0];
simStateCompliance = 'UnknownSimState';
function sys=mdlDerivatives(t,x,u)
sys = u;
function sys=mdlUpdate(t,x,u)
sys=[];
function sys=mdlOutputs(t,x,u)
sys=x;
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 0.01; % Example, set the next hit to be one second later.
sys = t + sampleTime;
function sys=mdlTerminate(t,x,u)
sys = [];
下面在Simulink界面下对S-函数封装为一个模块即可。
要注意的是,添加后需要双击这个s-function模块,输入名称即可。这里输入的名称必须要和你的函数名称保持一致,目的是为了让这个模块找到对应的代码去执行。

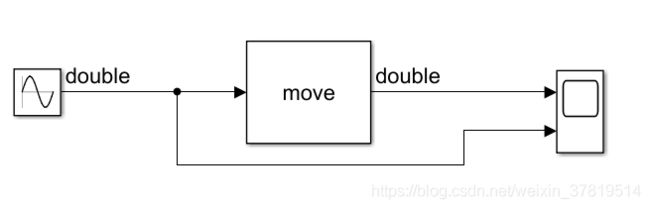
添加一个正弦模块和示波器,注意仿真时间为固定步长,间隔0.01s.正弦信号为sin(2t),观察输出信号。
搭建出来的模型如下:
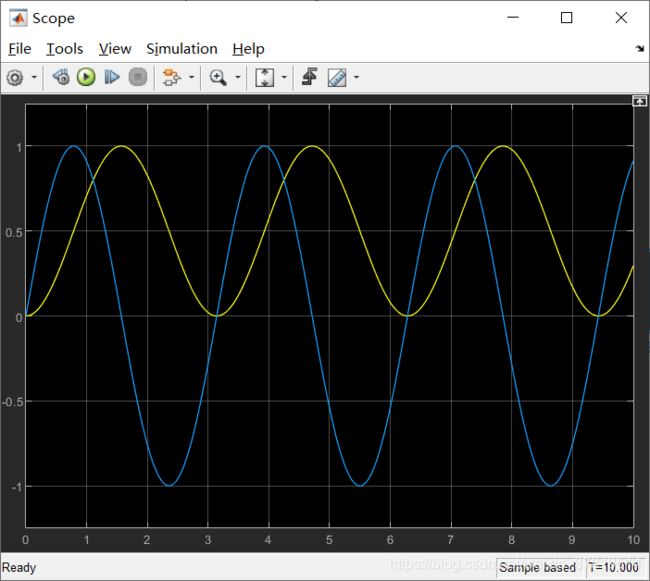
仿真运行的结果如下:
仿真结果分析
代码中描述这个系统的关键部位是这样写的:
function sys=mdlDerivatives(t,x,u)
sys = u;
…
…
function sys=mdlOutputs(t,x,u)
sys=x;
其中,mdlDerivatives(t,x,u)函数是计算状态变量的微分,也就是状态方程dx/dt = u;mdlOutputs(t,x,u)描述了输入、状态变量与输出之间的关系,也就是输出方程y = x。
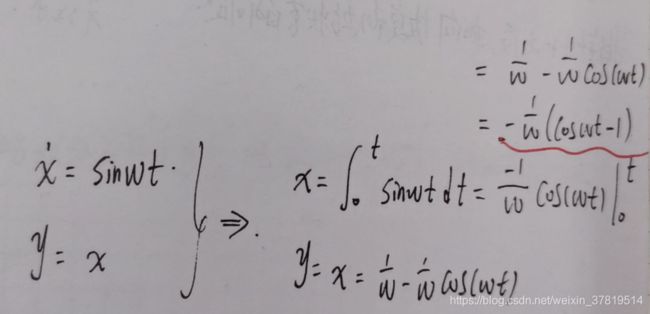
自己推导的公式,在matlab的输入面板下验证,代码如下,也可以验证得到相同的效果。
t = 0:0.01:10;u0 = sin(2t);
y = 0.5-0.5cos(2*t);plot(t,u0);hold on;plot(t,y);
参考资料
【1】:http://blog.sina.com.cn/s/blog_4b013fb10100nbdm.html
【2】:https://blog.csdn.net/u014183377/article/details/88757069?utm_medium=distribute.pc_relevant.none-task-blog-baidujs_title-0&spm=1001.2101.3001.4242
【3】:https://blog.csdn.net/Nirvana_Tai/article/details/105439610