实验1 线性回归 实操项目2——影厅观影人数预测(多变量线性回归)
实验内容:影厅观影人数预测
实验要求:
1.读取给定文件中数据集文件。(数据集路径:data/data72160/1_film.csv)
2.绘制影厅观影人数(filmnum)与影厅面积(filmsize)的散点图。
3.绘制影厅人数数据集的散点图矩阵。
4.选取特征变量与相应变量,并进行数据划分。
5.进行线性回归模型训练。
6.根据求出的参数对测试集进行预测。
7.绘制测试集相应变量实际值与预测值的比较。
8.对预测结果进行评价。
import numpy as np
import pandas as pd
from sklearn import datasets
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
from sklearn import metrics
from sklearn.metrics import r2_score
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
df = pd.read_csv('data/data72160/1_film.csv')
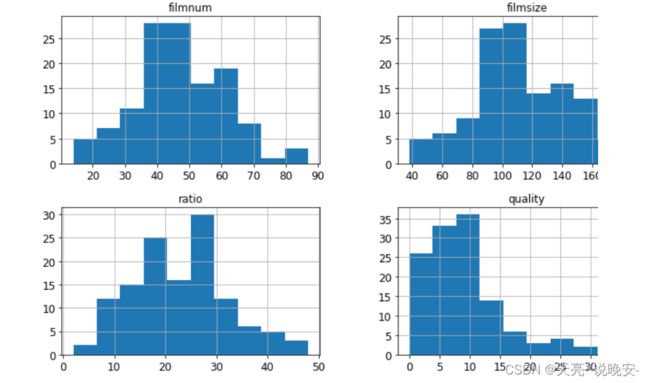
df.hist(xlabelsize=12,ylabelsize=12,figsize=(12,7))
plt.show()
"""
kind:图形类型
subplots=True:需要绘制多个子图
layout=(2,2):绘制子图数量2*2
sharex=False:子图不共享X轴
fontsize=8:字体大小
"""
df.plot(kind="density",subplots=True,layout=(2,2),sharex=False,fontsize=8,figsize=(12,7))
plt.show()
df.plot(kind='box',subplots=True,layout=(2,2),sharex=False,sharey=False,fontsize=8,figsize=(12,7))
plt.show()
names = ['filmnum','filmsize','ratio','quality']
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(correlations,vmin=0.3,vmax=1)
fig.colorbar(cax)
ticks = np.arange(0,4,1)
ax.set_xticks(ticks)
ax.set_yticks(ticks)
ax.set_xticklabels(names)
ax.set_yticklabels(names)
plt.show()
X = df.iloc[:,1:4]
y = df.filmnum
X = np.array(X.values)
y = np.array(y.values)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.25,random_state=1)
clf = LinearRegression()
clf.fit(X_train, y_train)
target = df.filmnum
df.columns
plt.figure(figsize=( 2*6, 5*5))
for i, col in enumerate(df.columns):
train_X = df.loc[:, col].values.reshape(-1, 1)
train_Y = target
linearmodel = LinearRegression()
reg = linearmodel.fit(train_X, train_Y)
score = reg.score(train_X, train_Y)
k = linearmodel.coef_
b = linearmodel.intercept_
x = np.linspace(train_X.min(), train_X.max(), 100)
y = k * x + b
plt.plot(x, y, c='red')
axes.set_title(col + ' Coefficient of determination:' + str(score))
plt.show()
"""
df:数据来源
figsize=(8,8):图形尺寸
c='b':散点图点的颜色
"""
pd.plotting.scatter_matrix(df,figsize=(8,8),c='b')
plt.show()
"""
:,1:4:代表选取数据集2-4列
"""
X = df.iloc[:,1:4]
y = df.filmnum
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.25,random_state=1)
print(X_train.shape,X_test.shape,y_train.shape,y_test.shape)
lr = LinearRegression()
lr.fit(X_train,y_train)
print('a={}\nb={}'.format(lr.coef_,lr.intercept_))
y_hat = lr.predict(X_test)
print(y_hat)
t = np.arange(len(X_test))
plt.plot(t,y_test,'r',linewidth=2,label='y_test')
plt.plot(t,y_hat,'g',linewidth=2,label='y_hat')
plt.legend()
plt.show()
print('R2_1={}'.format(lr.score(X_test,y_test)))
print('R2_2={}'.format(r2_score(y_test,y_hat)))
print('MAE={}'.format(metrics.mean_absolute_error(y_test,y_hat)))
print('MSE={}'.format(metrics.mean_squared_error(y_test,y_hat)))
print('RMSE={}'.format(np.sqrt(metrics.mean_squared_error(y_test,y_hat))))





(94, 3) (32, 3) (94,) (32,)
a=[ 0.37048549 -0.03831678 0.23046921]
b=4.353106493779009
[20.20848598 74.31231952 66.97828797 50.61650336 50.53930128 44.72762082
57.00320531 35.55222669 58.49953514 19.43063402 27.90136964 40.25616051
40.81879843 40.01387623 24.56900454 51.36815239 38.97648053 39.25651308
65.4877603 60.82558336 54.29943364 40.45641818 29.69241868 49.29096985
44.60028689 48.05074366 35.23588166 72.29071323 53.79760562 51.94308584
46.42621262 73.37680499]

R2_1=0.8279404383777595
R2_2=0.8279404383777595
MAE=4.63125112009528
MSE=46.638222814565964
RMSE=6.829218316510753






