datawhale 10月学习——树模型与集成学习：集成模式

前情回顾

1. 决策树
2. CART树的实现

结论速递

本章节从误差的来源入手，结合数学公式推导，了解了集成模型的目的，随后学习了集成学习的几种方法，分别是基础的bagging和boosting，还有stacking和blending，并对stacking进行了代码实现。
对思考题的解答融入在了笔记中。

1 集成的目的

1.1 误差的来源

我们所训练的模型，是在有限数据上训练得到的模型，这个模型必然与真实的产生数据的模型有出入。此时使用这个模型去预测新的数据，我们希望模型在新数据下的预测损失可以较小。（这里的预测损失可以指分类问题的错判率或回归问题的均方误差等各类评价指标）

从数学推导的角度，误差的来源可以解释如下

对于实际问题中的数据，我们可以认为它总是由某一个分布$p$生成得到的，我们不妨设训练集合上有限的$n$个样本满足
$${\text{X}}_1,{\text{X}}_2,...,{\text{X}}_n\sim p(\text{X})$$
而这些样本对应的标签是通过真实模型$f$和噪声${ϵ}_1,{ϵ}_2,...,{ϵ}_n$得到的，即
$$y_i=f({\text{X}}_i)+{ϵ}_i,i\in \{1,2,...,n\}$$
其中，假设噪声均值为$0$且方差为${\sigma }^2$。此时，我们得到了一个完整的训练集$D=\{({\text{X}}_1,y_1),({\text{X}}_2,y_2),...,({\text{X}}_n,y_n)\}$。对于新来的样本$\tilde{\text{X}}\sim p(\text{X})$，我们需要对其标签$y=f({\text{X}}_i)+{ϵ}_i$进行预测，假设当前处理的是回归问题，应学习一个模型$\hat{f}$使得平方损失$(y-\hat{f}(\tilde{\text{X}}){)}^2$尽可能地小。

需要注意的是$\hat{f}$不仅是$\tilde{\text{X}}$的函数，它是从训练集上得到的，训练集是从总体分布随机生成的有限分布，记为${\hat{f}}_D(\tilde{\text{X}})$。故我们想要一个稳定的函数，本质上优化的是$L={\mathbb{E}}_D(y-{\hat{f}}_D(\tilde{\text{X}}){)}^2$

为了进一步研究$L$，我们把模型（基于不同数据集对新样本特征）的平均预测值信息${\mathbb{E}}_D[{\hat{f}}_D(\tilde{\text{X}})]$添加到$L$中，此时存在如下分解【思考题】
$$\begin{array}{rl}L(\hat{f})& ={\mathbb{E}}_D(y-{\hat{f}}_D{)}^2\\ & ={\mathbb{E}}_D(f+ϵ-{\hat{f}}_D+{\mathbb{E}}_D[{\hat{f}}_D]-{\mathbb{E}}_D[{\hat{f}}_D]{)}^2\\ & ={\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D])+({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D)+ϵ{]}^2\\ & ={\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D]{)}^2]+{\mathbb{E}}_D[({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D{)}^2]+{\mathbb{E}}_D[{ϵ}^2]+2{\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D])({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D)]+2{\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D])ϵ]+2{\mathbb{E}}_D[({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D)ϵ]\\ & ={\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D]{)}^2]+{\mathbb{E}}_D[({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D{)}^2]+{\mathbb{E}}_D[{ϵ}^2]\\ & =[f-{\mathbb{E}}_D[{\hat{f}}_D]{]}^2+{\mathbb{E}}_D[({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D{)}^2]+{\sigma }^2\end{array}$$
其中$ϵ$和$({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D)$，$(f-{\mathbb{E}}_D[{\hat{f}}_D])$均相互独立，且${\mathbb{E}}_D[ϵ]=0$，故${\mathbb{E}}_D[({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D)ϵ]=0$，${\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D])ϵ]=0$。同样，${\mathbb{E}}_D[({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D)]=0$，故${\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D])({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D)]=0$

预测数据产生的平均损失来自于三项。其中，第一项为数据真实值与模型平均预测值的偏差，偏差越小则代表模型的学习能力越强，能够较好地拟合数据，第二项为模型预测值的方差（我们要记住$\hat{f}$应视作随机变量$D$的函数，故$\hat{f}$是随机变量），方差越小则代表模型的抗干扰能力越强，不易因为数据的扰动而对预测结果造成大幅抖动，第三项为数据中的原始噪声，它是不可能通过优化模型来降解的。这种分解为我们设计模型提供了指导，即可以通过减小模型的偏差来降低测试数据的损失，也可以通过减少模型的预测方差来降低损失。

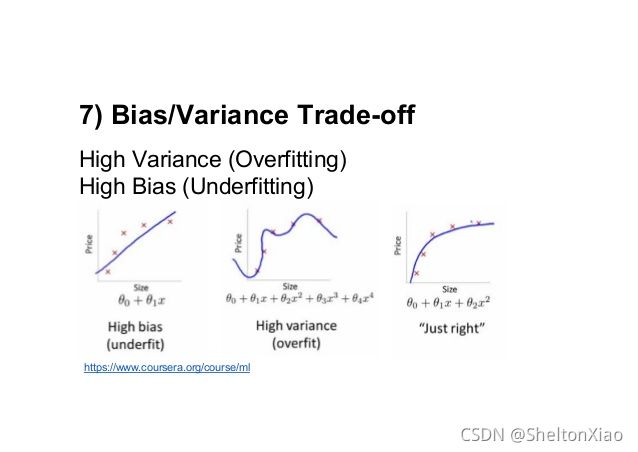
1.2 方差和偏差

可以用下面的靶子图形象地表明方差和偏差的含义。

对于一个具体的学习问题，

过于简单的学习器虽然抗干扰能力强，但由于不能充分拟合数据却会造成大的偏差，从而导致总的期望损失较高；
过于复杂的学习器虽然其拟合能力很强，但由于学习了多余的局部信息，因此抗干扰能力较弱造成较大的方差，从而导致总的期望损失较高。

【思考题】有人说Bias-Variance Tradeoff就是指“一个模型要么具有大的偏差，要么具有大的方差”，你认为这种说法对吗？你能否对“偏差-方差权衡”现象做出更准确的表述？
这种说法是不对的。二者可以取得折中，因为我们需要的是一个总体误差小的模型，单独期许偏差小，或者方差小都是不实际的。所谓偏差-方差权衡，就是我们要找到一个总体误差小的模型，为了使总体误差较小，这个模型既不能过于复杂（方差太大），也不能过于简单（误差太大）。下图可以很好地说明。但可以发现的是，即使是traderoff，也无法实现方差和误差都很小。

1.3 集成的意义

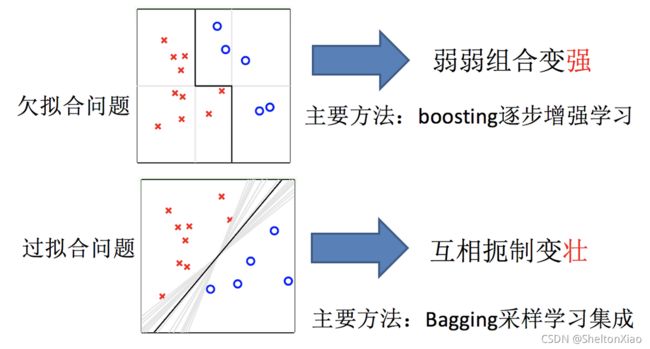
对单个学习器的偏差和方差的降解存在难度，那能否使用多个学习器进行结果的集成以进一步减小损失呢？

更明确地说，我们希望利用多个低偏差的学习器进行集成来降低模型的方差，或者利用多个低方差学习器进行集成来降低模型的偏差。

2 bagging和boosting

2.1 bagging

基本思路是利用多个低偏差的学习器进行集成来降低模型的方差。

bagging是一种并行集成方法，其全称是bootstrap aggregating，即基于bootstrap抽样的聚合算法。

自助采样法（Bootstap sampling），即对于m个样本的原始训练集，我们每次先随机采集一个样本放入采样集，接着把该样本放回，也就是说下次采样时该样本仍有可能被采集到，这样采集m次，最终可以得到m个样本的采样集，由于是随机采样，这样每次的采样集是和原始训练集不同的，和其他采样集也是不同的。
就是有放回的抽样。
Bootstrap是一类非参Monte Carlo方法，其实质是对观测信息进行再抽样，进而对总体的分布特性进行统计推断。首先，Bootstrap通过重抽样，避免了Cross-Validation造成的样本减少问题，其次，Bootstrap也可以创造数据的随机性。Bootstrap是一种有放回的重复抽样方法，抽样策略就是简单的随机抽样。

假设我们处理的是回归任务，并且每个基学习器输出值$y^{(i)}$的方差为${\sigma }^2$，基学习器两两之间的相关系数为$\rho$，则可以计算集成模型输出的方差为

$$\begin{array}{rl}Var(\hat{y})& =Var(\frac{{\sum }_{i=1}^M{y}^{(i)}}{M})\\ & =\frac{1}{M^2}[\sum _{i=1}^{M}Var(y^{(i)})+\sum _{i\ne j}Cov(y^{(i)},y^{(j)})]\\ & =\frac{1}{M^2}[M{\sigma }^2+M(M-1)\rho {\sigma }^2]\\ & =\rho {\sigma }^2+(1-\rho )\frac{{\sigma }^2}{M}\end{array}$$

当基模型之间的相关系数为1时方差不变，这相当于模型之间的输出完全一致，必然不可能带来方差的降低。bootstrap的放回抽样特性保证了模型两两之间很可能有一些样本不会同时包含，这使模型的相关系数得以降低，而集成的方差随着模型相关性的降低而减小，如果想要进一步减少模型之间的相关性，那么就需要对基学习器进行进一步的设计。

【思考题】假设总体有$100$个样本，每轮利用bootstrap抽样从总体中得到$10$个样本（即可能重复），请求出所有样本都被至少抽出过一次的期望轮数。（通过本文介绍的方法，我们还能得到轮数方差的bound）

2.2 Boosting

基本思路是利用多个低方差学习器进行集成来降低模型的偏差。

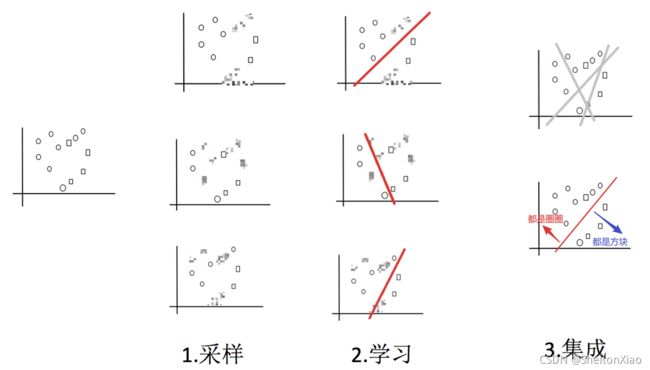
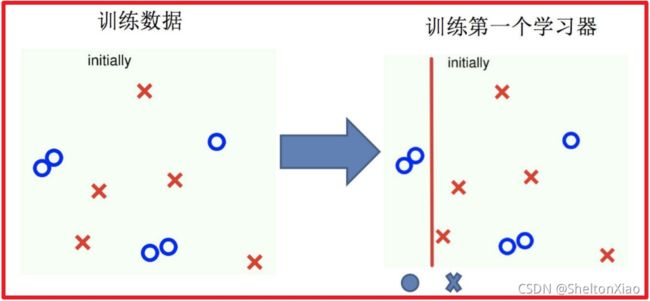
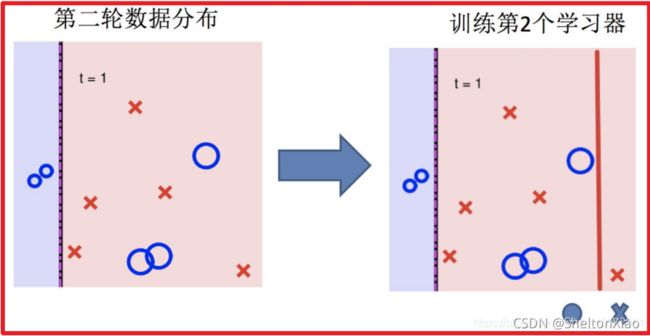
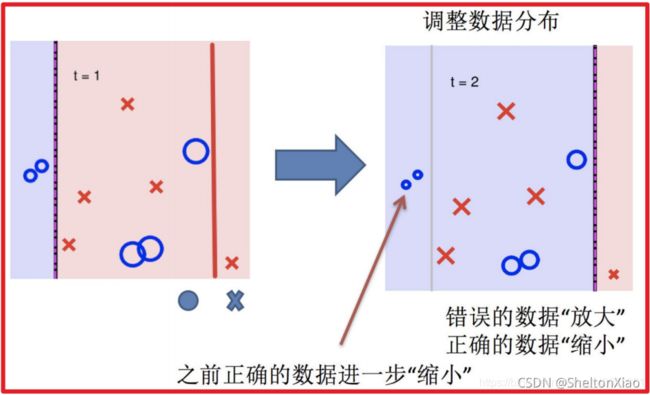
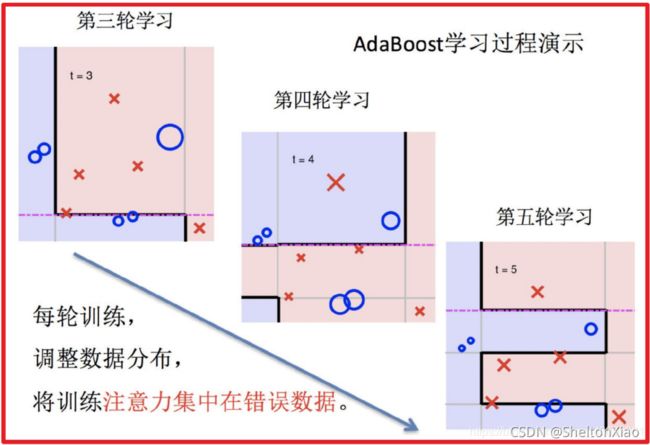
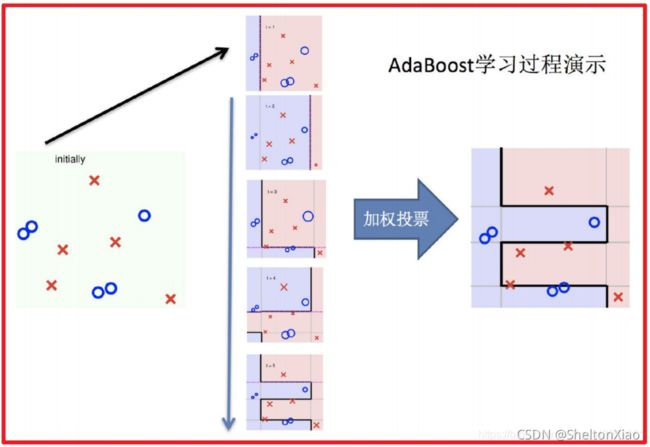
Boosting的过程可以如下图表示（来源于博客）。

3 stacking与blending

3.1 stacking

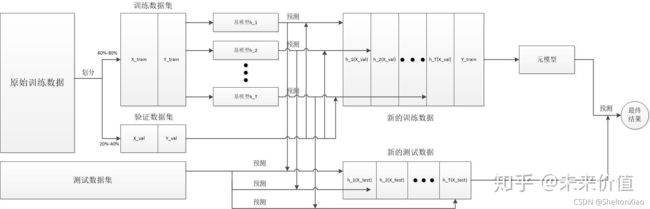
stacking本质上也属于并行集成方法，但其并不通过抽样来构造数据集进行基模型训练，而是采用K折交叉验证。

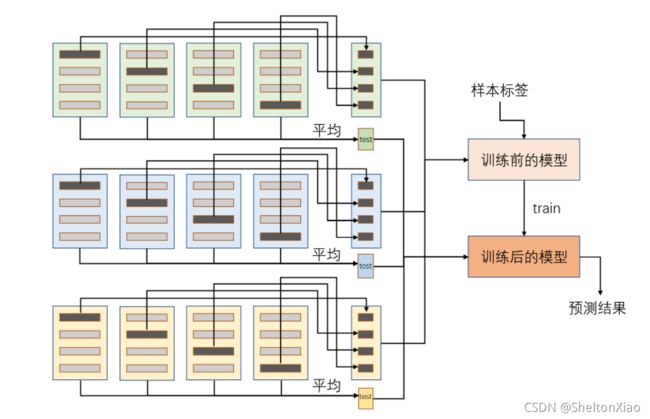
整个stacking的流程如下图所示，我们在3种基学习器使用4折交叉验证，因此图中的左侧部分需要12次训练，右侧的浅红色和深红色表示的是同一个最终模型，使用不同颜色是为了主要区分训练前和训练后的状态。这里需要注意的是，整个集成模型一共包含了25次预测过程，即每个基模型对各折数据的预测、每个基模型对测试集数据的预测以及最终模型的1次预测。

【思考题】对于stacking和blending集成而言，若m个基模型使用k折交叉验证，此时分别需要进行几次训练和几次预测？
需要进行$m\times k$次训练，$m\times 2k+1$次预测。

下图来自集成学习–Bagging、Boosting、Stacking、Blending。

3.2 blending

blending集成与stacking过程类似，它的优势是模型的训练次数更少，但其缺陷在于不能使用全部的训练数据，相较于使用交叉验证的stacking稳健性较差。

就是不用交叉验证的stacking，其他流程和stacking一致。

下图来自集成学习–Bagging、Boosting、Stacking、Blending。

3.3 stacking的代码实现

先导入常用库。

from sklearn.model_selection import KFold
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
from sklearn.svm import LinearSVR
from sklearn.datasets import make_regression

import numpy as np
import pandas as pd

基回归器和最终回归器初始化。

m1 = KNeighborsRegressor()
m2 = DecisionTreeRegressor()
m3 = LinearRegression()

final_model = LinearSVR()

总共初始化了3个基回归器。

models = [m1,m2,m3]

k = 4
m = len(models)

训练和测试数据生成。

X, y = make_regression(n_samples = 1000, n_features = 8, n_informative = 4, random_state = 33)
test_X, _ = make_regression(n_samples = 500, n_features = 8, n_informative = 4, random_state = 33)

主要过程如下，对每一个基回归器，都进行k折交叉验证训练，并预测对应的结果，作为最终回归器的训练集；同时对测试数据进行预测，取平均作为最终回归器的测试集。

final_train = pd.DataFrame(np.zeros((X.shape[0],m)))
final_test = pd.DataFrame(np.zeros((test_X.shape[0],m)))

kf = KFold(n_splits=k)
for model_id in range(m):
  model = models[model_id]
  for train_index, test_index in kf.split(X):
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]
    model.fit(X_train, y_train)
    final_train.iloc[test_index, model_id] = model.predict(X_test)
    final_test.iloc[:, model_id] += model.predict(test_X)
  final_test.iloc[:,model_id] /= m

final_model.fit(final_train,y)
res = final_model.predict(final_test)

4 知识回顾

1. 什么是偏差和方差分解？偏差是谁的偏差？此处的方差又是指什么？
   偏差和方差分解公式如下：
   $$\begin{array}{rl}L(\hat{f})& ={\mathbb{E}}_D(y-{\hat{f}}_D{)}^2\\ & ={\mathbb{E}}_D(f+ϵ-{\hat{f}}_D+{\mathbb{E}}_D[{\hat{f}}_D]-{\mathbb{E}}_D[{\hat{f}}_D]{)}^2\\ & ={\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D])+({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D)+ϵ{]}^2\\ & ={\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D]{)}^2]+{\mathbb{E}}_D[({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D{)}^2]+{\mathbb{E}}_D[{ϵ}^2]+2{\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D])({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D)]+2{\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D])ϵ]+2{\mathbb{E}}_D[({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D)ϵ]\\ & ={\mathbb{E}}_D[(f-{\mathbb{E}}_D[{\hat{f}}_D]{)}^2]+{\mathbb{E}}_D[({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D{)}^2]+{\mathbb{E}}_D[{ϵ}^2]\\ & =[f-{\mathbb{E}}_D[{\hat{f}}_D]{]}^2+{\mathbb{E}}_D[({\mathbb{E}}_D[{\hat{f}}_D]-{\hat{f}}_D{)}^2]+{\sigma }^2\end{array}$$
   其中偏差是指真实值与模型平均预测结果的差距，偏差越小，模型预测能力越强；方差是指模型预测值的方差，方差越小，模型预测越稳定。
2. 相较于使用单个模型，bagging和boosting方法有何优势？
   bagging利用多个低偏差的学习器进行集成来降低模型的方差，boosting利用多个低方差学习器进行集成来降低模型的偏差。
3. 请叙述stacking的集成流程，并指出blending方法和它的区别。
   第一步：使用训练数据，训练T个不同的模型，得到T个基模型。
   第二步：使用T个基模型，分别对训练数据k折交叉验证，与原始训练数据的标签一起组成新的训练数据。
   第三步：使用T个基模型，分别对测试数据进行预测，生成新的测试数据。
   第四步：使用新的训练数据，训练一个元模型。
   第五步：使用元模型对测试数据进行预测，得到最终结果。
   blending方法在第二步对训练数据直接进行训练和预测，没有进行k折交叉验证。

参考阅读

1. 一文读懂集成学习
2. 集成学习–Bagging、Boosting、Stacking、Blending
3. 【史诗级干货长文】集成学习算法
4. 为什么说bagging是减少variance，而boosting是减少bias?