ON LARGE-BATCH TRAINING FOR DEEP LEARNING: GENERALIZATION GAP AND SHARP MINIMA
关于深度学习的大批训练:generalization gap &sharp
ABSTRACT
随机梯度下降(SGD)方法及其变体是许多深度学习任务的选择算法。这些方法在小批量的情况下运行,其中一小部分训练数据,比如32-512个数据点,被采样来计算梯度的近似值。在实践中已经观察到,当使用较大的批处理时,模型的质量会下降,这可以通过模型的泛化能力来衡量。**我们研究了在大批量情况下泛化下降的原因,并给出了支持大批量方法趋向于收敛于训练和测试函数的急剧极小值这一观点的数值证据,**众所周知,急剧极小值导致较差的泛化。相比之下,小批量方法始终收敛于平面最小化器,我们的实验支持一个普遍的观点,即这是由于梯度估计中的固有噪声造成的。我们讨论了几种策略,试图帮助大批量方法消除这种泛化差距。
- INTRODUCTION
深度学习已经成为大规模机器学习的基石之一。深度学习模型被用于在包括计算机视觉、自然语言处理和强化学习在内的各种任务上取得最先进的结果;参见(Bengio et al., 2016)及其参考文献。这些网络的训练问题是非凸优化问题之一。数学上,这可以表示为
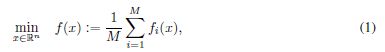
其中fi为数据点i2f1的损失函数;2;;Mg表示模型预测与数据的偏差,x为待优化权重向量。优化这一功能的过程也称为网络训练。随机梯度下降(SGD) (Bottou, 1998;Sutskever et al., 2013)及其变体通常用于训练深度网络。这些方法通过迭代地采取形式的步骤来最小化目标函数f:
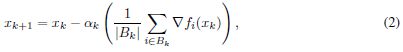
Bk 属于1;2;;M为从数据集中采样的批次,k为迭代k时的步长,这些方法可以解释为使用有噪声梯度的梯度下降,通常称为带有批次大小jBkj的小批次梯度。SGD和它的变种被用在一个小批量的制度,其中jBkj 远小于M和典型的jBkj 属于32;64;;512。这些配置在实践中已成功地应用于大量应用中;参见e.g. (Simonyan & Zisserman, 2014;Graves等,2013;Mnih等,2013)。这些方法的许多理论性质是已知的。这些保证包括:(a)强凸函数的收敛性和非凸函数的不动点收敛性(Bottou et al., 2016), (b)鞍点避免(Ge et al., 2015);Lee等(2016)和©输入数据的鲁棒性(Hardt等,2015)。然而,**随机梯度方法有一个主要的缺点:由于迭代的顺序性和批量小,并行化的途径有限。**同时,也有一些努力将SGD与深度学习并行化(Dean et al., 2012;Das等,2016;Zhang et al., 2015),获得的速度和可伸缩性往往受到小批量大小的限制。**提高并行性的一个自然途径是增加批处理大小jBkj。这增加了每次迭代的计算量,可以有效地分布。然而,实践者发现这导致泛化性能的损失;参见例(LeCun et al., 2012)。换句话说,与小批方法相比,使用大批方法训练的模型在测试数据集上的性能往往更差。在我们的实验中,我们发现即使对于较小的网络,泛化的下降(也称为泛化间隙)也高达5%。本文给出的数值计算结果说明了大批量方法的这一缺陷。我们观察到泛化间隙与大批量方法得到的极小化器的显著锐度相关。这激发了修复泛化问题的努力,因为在不牺牲泛化性能的情况下使用大量的训练算法将能够扩展到比目前可能的更多的节点。这可能会大大减少训练时间;**我们在附录C中提供了一个理想化的性能模型来支持这种说法。。。。论文组织如下。。。。在本节的其余部分中,我们定义了本文使用的符号,并在第2节中介绍了我们的主要发现及其支持的数字证据。在第3节中,我们探讨了小批量方法的性能,在第4节中,我们简要讨论了我们的结果与最近的理论工作之间的关系。最后,我们提出了一些开放的问题,涉及泛化差距、急剧极小值和使大规模培训可行的可能修改。在附录E中,我们提出了一些解决大批量培训问题的尝试。 - NOTATION
我们使用符号fi来表示损失函数和第i个数据点对应的预测函数的组成。权重向量用x表示,下标k表示迭代。我们使用术语小批量(SB)方法来表示SGD,或其变体之一,如ADAM (Kingma &(Ba, 2015)和ADAGRAD (Duchi et al., 2011),条件是梯度近似是基于一个小的小批量。在我们的设置中,批量Bk是随机采样的,每次迭代都保持其大小不变。我们使用术语big -batch (LB)方法来表示任何使用大型微型批处理的训练算法。在我们的实验中,ADAM被用来探索小批量或大批量方法的行为。 - DRAWBACKS OF LARGE-BATCH METHODS
- OUR MAIN OBSERVATION
如第1节所述,从业者在使用大批量方法训练深度学习模型时发现了泛化的差距。有趣的是,尽管大批方法通常产生与小批方法类似的训练函数值,但这是不存在的。造成这种现象的原因可能有以下几点:**(1)LB方法对模型过拟合;LB方法被吸引到鞍点;(三)LB方法缺乏SB方法的探索性,容易在最接近初始点的极小点上放大;(iv) SB和LB方法收敛于具有不同泛化性质的定性不同的极小化器。**本文提供的数据支持后两个猜想。本文的主要观察结果如下
缺乏泛化能力是由于大批量方法往往收敛到训练函数的急剧极小值。这些极小化器的特征是r2f(x)中有大量的正特征值,且泛化效果较差。相比之下,小批量方法收敛于具有大量小特征值r2f(x)的平面极小化方法。我们观察到,深度神经网络的损失函数景观是这样的,大的批量方法被吸引到具有敏锐极小值的区域,而不像小批量方法,无法逃脱这些极小值方法的吸引
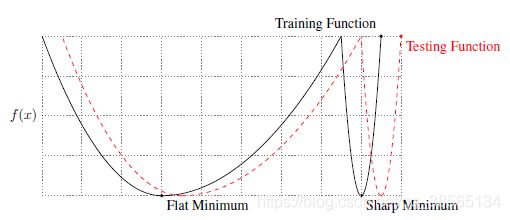
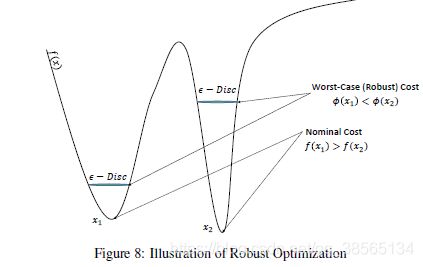
在统计学和机器学习文献中,已经讨论过锐化和平面最小化器的概念。(Hochreiter & Schmidhuber, 1997)(非正式地)将平面极小化器x定义为函数在相对较大的x邻域内变化缓慢的函数。平面最小值可以用较低的精度来描述,而尖锐最小值则需要较高的精度。训练函数在极大极小值处的敏感性对训练模型对新数据的泛化能力有负面影响;请参见图1中的假想说明。这可以通过最小描述长度(MDL)理论来解释,该理论指出,统计模型需要更少的比特来描述(即,具有较低的复杂度)泛化较好(Rissanen, 1983)。由于平面极小化器的指定精度比尖锐极小化器的指定精度低,因此它们往往具有更好的泛化性能。通过贝叶斯学习观(MacKay, 1992)和自由吉布斯能量的视角,给出了其他解释;参见Chaudhari等人。
- NUMERICAL EXPERIMENTS
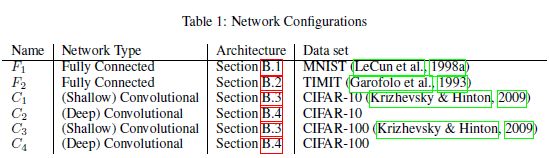
在本节中,我们提供数值结果来支持上述观察。为此,我们利用了(Goodfellow et al., 2014b)所使用的可视化技术和提出的启发式锐度度量(式(4))。在实验中考虑了6种多类分类网络结构;如表1所示。有关数据集和网络配置的详细信息分别载于附录A和附录B。由于这类问题的普遍存在,我们使用平均交叉熵损失作为目标函数f。选择这些网络是为了举例说明在实践中使用的流行配置,如AlexNet (Krizhevsky et al., 2012)和VGGNet (Simonyan & Zisserman, 2014)。在其他网络上以及使用其他初始化策略、激活函数和数据集上的结果显示了类似的行为。****
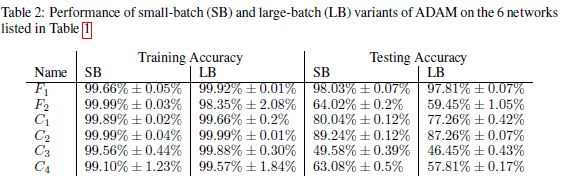
对于所有的实验,我们使用10%的训练数据作为批量大实验的批量大小,使用256个数据点作为小批量实验的批量大小。我们对这两种机制都使用了ADAM优化器。使用其他优化器进行大批量实验,包括ADAGRAD (Duchi et al., 2011)、SGD (Sutskever et al., 2013)和adaQN (Keskar & .)Berahas(2016)也得出了类似的结果。所有的实验都是从不同的(均匀分布随机)起点进行了5次,我们报告了测量量的平均值和标准偏差。我们设置的基准性能如表2所示。由此可以看出,在所有的网络中,两种方法都具有较高的训练精度,但泛化性能存在显著差异。这些网络在没有任何预算或限制的情况下得到训练,直到损失功能停止改善为止。
我们强调,泛化差距不是由于统计中常见的过度拟合或过度训练造成的。这种现象以测试精度曲线的形式表现出来,在一定的迭代峰值,然后由于训练数据的模型学习特性而衰减。这不是我们在实验中观察到的;F2和C1网络的训练测试曲线如图2所示,这两个网络代表了其余网络。因此,旨在防止模型过度拟合的早期停止启发式将无助于减少泛化差距。网络的训练精度和测试精度的差异是由于网络的具体选择(如AlexNet、VGGNet等),而不是本研究的重点。相反,我们的目标是在给定的网络模型上研究SB和LB两种机制测试性能差异的根源。

- PARAMETRIC PLOTS
我们首先给出了函数的参数一维图,如(Goodfellow et al., 2014b)所述。让x ?砂x ?分别用小批量和大批量运行ADAM得到的解决方案。在训练和测试数据集上,我们沿着包含两个点的线段绘制损失函数。具体来说,2[?1;函数f(x?’ + x(1?)? s)也将在中间点的分类精度;参见图31所示。在本实验中,我们从5个用于生成表2数据的试验中随机选择了一对SB和LB最小化器。从图中可以看出,在一维流形中,LB极小值明显地比SB极小值尖锐。图3中的图只探索了函数的一个线性切片,但是在附录D中的图7中,我们绘制了f(sin(2)x?’ + cos(2)x?s)沿两个极小值点之间的曲线路径监视函数。在这里,最小值的相对锐度也很明显。

- SHARPNESS OF MINIMA
到目前为止,我们已经松散地使用术语sharp minimizer,但是我们注意到这个概念已经在文献中得到了关注(Hochreiter &Schmidhuber, 1997)。**最小化器的锐度可以由r2f(x)特征值的大小来表征,**但是考虑到这种计算在深度学习应用中的高昂成本,我们采用了一种敏感性度量,尽管不完美,但在计算上是可行的,即使对于大型网络也是如此。它是基于研究一个解的一个小邻域,并计算函数f在该邻域内可以达到的最大值。我们使用该值来测量给定局部极小值下训练函数的灵敏度。现在,由于最大化过程是不精确的,为了避免被仅在Rn的一个很小的子空间中得到一个很大的f的情况所误导,我们在整个空间Rn中以及在随机流形中执行最大化。为此,我们引入了一个np矩阵A,它的列是随机生成的。这里p决定了流形的维数,在我们的实验中选择p = 100。具体地说,设C为解的一个方框,在这个方框上执行f的最大值,设2 Rnp为上面定义的矩阵。为了保证问题维数和稀疏性的锐度不变,我们将约束集C定义为
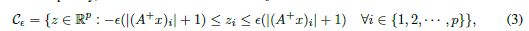
式中,A+表示A的伪倒数,从而控制框的大小。现在我们可以定义锐度(或灵敏度)的度量。
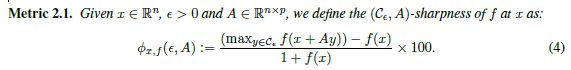
除非另有规定,否则我们使用此度量用于纸张其余部分的锐度;如果没有指定A,则假设为单位矩阵,In。(我们顺便注意到,在凸优化文献中,术语sharp minimum有一个不同的定义(Ferris, 1988),但是这个概念对我们的目的没有用处。)在表3和表4中,我们给出了各种问题最小化器的锐度指标(4)的值。表3探索了整个空间(即, A = In),而表4使用随机抽样的n 100维矩阵A。5 10 4).在所有的实验中,我们都不精确地利用L-BFGS-B的10次迭代求解式(4)中的最大化问题(Byrd et al., 1995)。这个迭代次数的限制是由于评估真正目标f的巨大成本所必需的。两个表都显示了SB和LB制度下我们的度量值之间的1-2个数量级的差异。这些结果进一步证明了大批量方法得到的解定义了训练函数敏感性较大的点。在序言部分,我们描述了试图解决LB方法泛化问题的方法。这些方法包括数据扩充、保守训练和对抗性训练。我们的初步发现表明,这些方法有助于减少泛化差距,但仍然导致相对尖锐的最小化,因此,不能完全解决问题。注意,度规2.1与r2f(x)的频谱密切相关。假设A足够小,当A = In时,值(4)与r2f(x)的最大特征值有关,当A随机采样时,它近似于r2f(x)投影到A的列空间上的Ritz值。
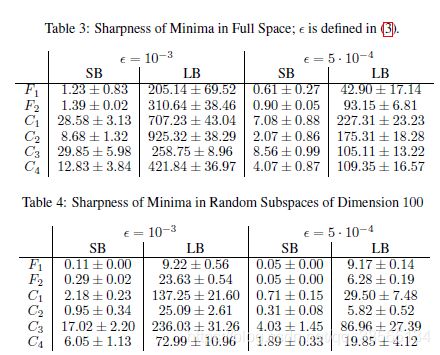
我们在总结本节时注意到,在我们的实验中确定的急剧极小值不像圆锥,即,函数不会沿着所有(甚至大多数)方向快速增长。通过对LB溶液邻域内的损失函数进行采样,我们发现损失函数只沿着一个很小的维子空间(例如整个空间的5%)急剧上升;在大多数其他方向上,函数是相对平坦的。 - SUCCESS OF SMALL-BATCH METHODS
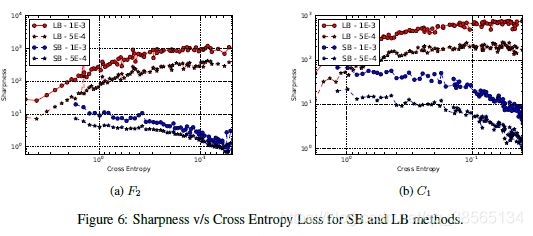
经常有报道说,当增加一个问题的批处理大小时,存在一个阈值,超过这个阈值,模型的质量就会下降。图4中可以观察到F2和C1网络的这种行为。在这两个实验中,都有一个批量大小(F2为15000个,C1为500个),之后测试精度会有很大的下降。还请注意,锐度值的向上漂移在此阈值附近显著减小。表1中的其他网络也存在类似的阈值。现在让我们考虑一下SB方法的行为,它在步长计算中使用有噪声的梯度。从上一节报告的结果可以看出,梯度中的噪声将迭代器推离了急剧极小化器的吸引池,并鼓励移动到更平坦的极小化器,在那里噪声不会导致从该池中退出。当批次大小大于上述阈值时,随机梯度中的噪声不足以引起初始盆地的喷射,从而收敛到更锋利的最小值。要更详细地探讨这个问题,请考虑下面的实验。我们使用批处理大小为256的ADAM对网络进行100个纪元的训练,并在每个纪元之后在内存中保留迭代。使用这100个迭代作为起点,我们使用LB方法对网络进行100个周期的训练,并接收100个负载(或暖启动)的大批解决方案。我们在图5中绘制的实验图支持这一观点:我们观察到kx的比值?年代?x0k2和kx吗?“?x0k2 3 - 10的范围。为了进一步说明SB法和LB法得到的解在定性上的差异,我们在图6中绘制了F2和C1网络的一次随机试验中,我们对损失函数(交叉熵)的锐度测量(4)。对于较大的损失函数值,即在初始点附近,SB法和LB法的锐度值相似。随着损失函数的减小,LB方法对应迭代的锐度迅速增加,而SB方法的锐度在初始阶段保持相对不变,然后逐渐减小,这表明探索阶段之后收敛到平坦极小值。这些大批量解决方案的测试精度和锐度,随着小批量迭代测试精度的提高而提高。注意,当预热开始时只有几个初始阶段,LB方法不会产生泛化改进。同时迭代的锐度也很高。另一方面,经过一定的预热时间后,大批量迭代的精度提高,锐度下降。显然,当SB方法结束了探索阶段并发现了一个平面最小化器时,就会发生这种情况;然后LB法可以收敛到它,使测试精度很好。据推测,LB方法倾向于被接近起始点x0的最小值所吸引,而SB方法则远离并定位较远的最小值。我们的数值实验支持这一观点:我们观察到kx的比值?年代?x0k2和kx吗?“?x0k2 3 - 10的范围。为了进一步说明SB法和LB法得到的解在定性上的差异,我们在图6中绘制了F2和C1网络的一次随机试验中,我们对损失函数(交叉熵)的锐度测量(4)。对于较大的损失函数值,即在初始点附近,SB法和LB法的锐度值相似。随着损失函数的减小,LB方法对应迭代的锐度迅速增加,而SB方法的锐度在初始阶段保持相对不变,然后逐渐减小,这表明探索阶段之后收敛到平坦极小值。


- DISCUSSION AND CONCLUSION
在本文中,我们提供了一些数值实验来支持这样一种观点,即收敛到尖锐的极小值点会导致用于深度学习的大批量方法泛化不良。为此,我们为各种深度学习架构提供了一维参数图和扰动(锐度)度量。在附录E中,我们描述了我们试图纠正这个问题,包括数据扩充、保守训练和鲁棒优化。我们的初步调查表明,这些策略并没有纠正问题;它们改进了大批量方法的泛化,但仍然导致相对尖锐的极小值。另一个可能的补救措施包括使用动态抽样,随着迭代的进展,批处理大小逐渐增加(Byrd et al., 2012;弗里德兰德,施密特,2012)。通过我们的热启动实验(见图5)可以看出这种方法的潜在可行性,其中使用大批量方法即热启动小批量方法可以获得较高的测试精度。近年来,许多学者描述了深神经网络损失面有趣的理论性质;参见e.g. (Choromanska et al., 2015;Soudry,卡,2016;Lee等,2016)。他们的工作表明,在一定的规律性假设下,深度学习模型的损失函数充满了许多局部极小值,其中许多极小值对应于一个相似的损失函数值。我们的结果与这些观察结果一致,因为在我们的实验中,锐化和平化的最小值都有非常相似的损失函数值。然而,我们不知道上述理论模型是否提供了关于损耗面锐极小化器存在和密度的信息。我们的研究结果提出了一些问题:(a)能否证明大规模(LB)方法通常收敛于深度学习训练函数的急剧最小化?(本文仅提供了一些数值证据);(b)这两种极小值的相对密度是多少?©是否可以设计适合于LB方法性质的各种任务的神经网络结构?(d)能否以使LB方法能够成功的方式初始化网络?(e)是否可能通过算法或管制手段,使LB方法避开尖锐的极小值方法 - REFERENCES
- A DETAILS ABOUT DATA SETS
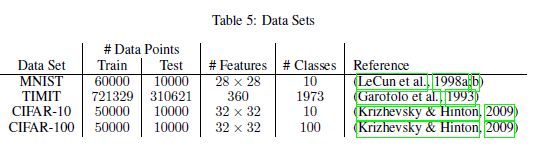
我们在表5中总结了实验中使用的数据集。TIMIT是一个语音识别数据集,使用Kaldi (Povey et al., 2011)进行预处理,使用全连接网络进行训练。其余的数据集无需任何预处理即可使用。
- B ARCHITECTURE OF NETWORKS
- B.1 NETWORK F1
对于这个网络,我们使用一个784维的输入层,然后是5个批处理规范化(Ioffe &
Szegedy, 2015)每层有512个神经元被ReLU激活。输出层由10个具有softmax激活的神经元组成。 - B.2 NETWORK F2
F2的网络结构类似于F1。我们使用一个360维的输入层,然后是由512个神经元组成的7个批量归一化层,其中ReLU被激活。输出层由1973个具有softmax激活的神经元组成。 - B.3 NETWORKS C1 AND C3
C1网络是流行的AlexNet配置的修改版本(Krizhevsky et al., 2012)。为简便起见,表示滤波器的n个卷积层的堆栈和步长为d的b c内核大小为n[a];b;c;d]。C1配置使用2组[64;5;5;2] MaxPool(3),其次是2个致密层尺寸(384;192)最后,输出层的大小为10。我们对所有层和ReLU激活都使用batchnormalization。我们还使用了两个致密层0:5保留概率的Dropout (Srivastava et al., 2014)。配置C3与C1相同,只是它使用100个softmax输出,而不是10个。 - B.4 NETWORKS C2 AND C4
C2网络是流行的VGG配置(Simonyan &Zisserman, 2014)。C3网络采用的配置为:2[64;3;3;1);2 (128;3;3;1);3 (256;3;3;1);3 (512;3;3;1);3 (512;3;3;1]每个堆栈之后的MaxPool(2)。这个堆栈后面是一个512维的密集层,最后是一个10维的输出层。各层的活化和性质如B.3所示。与C3和C1一样,配置C4与C2相同,只是它使用100个softmax输出,而不是10个。 - C PERFORMANCE MODEL
正如在第1节中提到的,在没有泛化间隙的情况下在大批处理情况下运行的训练算法将能够扩展到比目前可能的更多的节点。这样的算法也可以通过更快的收敛速度来提高训练时间。我们提出了一个理想化的性能模型来展示我们的目标。为了使LB方法能够与SB方法竞争,LB方法必须(i)收敛到能够很好地推广的最小值,并且(ii)在合理次数的迭代中完成它,我们在这里进行了分析。令Is和I '分别为SB方法和LB方法达到可比较测试精度点所需的迭代次数。设B和B '为对应的批次大小,P为用于培训的处理器数量。设P < B ',设fs§为SB方法的并行效率。为简便起见,我们假设LB方法的并行效率f ’ §为1:0。换句话说,我们假设LB方法是完全可伸缩的,因为使用了大量的批处理大小。为了使LB比SB快,我们必须这样做
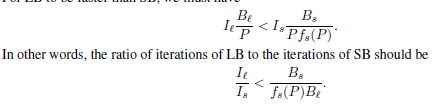
例如,如果fs§ = 0:2和Bs=B ’ = 0:1, LB方法必须收敛于SB方法的至多一半迭代次数,才能看到性能优势。我们请读者参考(Das et al., 2016)以获得更详细的模型,并评论批大小对性能的影响。 - CURVILINEAR PARAMETRIC PLOTS

- ATTEMPTS TO IMPROVE LB METHODS
在这一节中,我们讨论了一些策略,旨在解决大规模方法泛化不良的问题。在第2节中,我们使用10%作为大批实验的批大小百分比,使用256作为小批方法的批大小百分比。对于所有实验,我们都使用ADAM作为优化器,而不考虑批大小。 - E.1 DATA AUGMENTATION
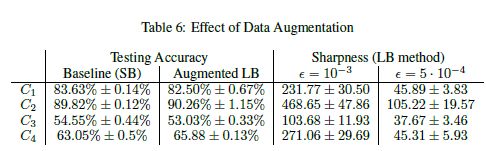
考虑到大批量方法似乎更倾向于使用锋利的最小化器,我们可以问是否可以修改损失函数的几何结构,使其对大批量方法更友好。损失函数既取决于目标函数的几何形状,也取决于训练集的大小和性质。我们考虑的一种方法是数据增强;参见e.g. (Krizhevsky et al., 2012;Simonyan,Zisserman, 2014)。这种技术的应用是特定于领域的,但通常涉及通过对训练数据进行受控修改来扩充数据集。例如,在图像识别的情况下,可以通过平移、旋转、剪切和翻转训练数据来扩充训练集。该技术实现了网络的正规化,并被用于提高多个数据集的测试精度。在我们的实验中,我们使用积极的数据增强训练了4个基于图像的(卷积)网络,结果如表6所示。对于增强,我们使用水平反射,随机旋转多达10倍和随机平移高达0:2倍的图像大小。从表中很明显,尽管LB方法达到准确度某人方法与训练数据增强(也),最小值的清晰度仍然存在,表明敏感图像包含在训练和测试集。在本节中,我们排除参数为某人情节和锐度值法由于空间限制和2.2节中给出的相似的。

- E.2 CONSERVATIVE TRAINING
在(Li et al., 2014)中,作者认为通过以下近似子问题得到迭代,可以提高大批量设置下SGD的收敛速度。
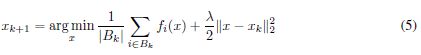
这种策略的动机是,在大批方法的上下文中,在转移到下一个批方法之前更好地利用该批方法。利用梯度下降法、坐标下降法或L-BFGS法等3 ~ 5次迭代法求解最小值问题。(Li et al., 2014)报告指出,这不仅提高了SGD的收敛速度,还提高了凸机器学习问题的经验性能。利用批处理的基本思想并不是针对凸问题的,我们可以将同样的框架应用于深度学习,但是没有理论保证。事实上,(Zhang et al., 2015)和(Mobahi, 2016)中也提出了类似的算法用于深度学习。前者强调小批量SGD的并行性和异步性,后者强调训练的扩散性-连续性机制。使用保守训练方法的结果如图7所示。在所有的实验中,我们使用ADAM的3次迭代来解决问题(5),并将正则化参数设置为10 3。同样,大批量方法的检测精度有统计学上的显著提高,但并没有解决敏感性问题。 - E.3 ROBUST TRAINING
避免急剧极小值的一种自然方法是通过鲁棒优化技术。这些方法试图优化最坏情况下的成本,而不是名义(或真实)成本。在数学上,给定>,这些技术可以解决问题
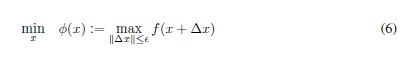
几何上,经典(名义)优化试图找到一个山谷的最低点,而鲁棒优化试图降低一个-盘沿损失表面。我们希望有兴趣的读者参考(Bertsimas et al., 2010)和其中的参考文献,以回顾非凸鲁棒优化。然而,这种技术的直接应用在我们的上下文中是不可行的,因为每次迭代都非常昂贵,因为它涉及到求解大规模二阶二次二次曲线程序(SOCP)
在深度学习环境中,有两种相互依赖的鲁棒性形式:对数据的鲁棒性和对解决方案的鲁棒性。前者利用了函数f本质上是一个统计模型这一事实,而后者将f视为一个黑盒函数。在(Shaham et al., 2015)中,作者证明了解决方案的鲁棒性(相对于数据)与对抗性训练之间的等价性(Goodfellow et al., 2014a)。考虑到数据增强策略的部分成功,质疑对抗性训练的有效性是很自然的。如(Goodfellow et al., 2014a)所述,对抗训练也旨在人为地增加训练集,但与随机数据增强不同的是,它使用模型s敏感性构建新的例子。尽管其直观的吸引力,在我们的实验中,我们发现这种策略并没有提高泛化。同样,我们也没有观察到(Zheng et al., 2016)提出的稳定性训练对泛化的好处。在这两种情况下,测试精度、锐度值和参数图都与第2节中讨论的未修改(基线)情况相似。对抗性训练(或任何其他形式的健壮训练)是否能提高大规模训练的生存能力还有待观察。