关联规则之 Apriori 算法实现
一、数据预览
Apriori 算法是电商数据挖掘中的经典算法,用于发现商品之间的关联规则,例如买了 A 和 B 的情况下是否还会买 C,通过计算商品组合之间的支持度和置信度来实现。首先我们来看一张订单表,包含订单编号,和商品列表。如订单一表示同时购买了 A, B, E 三个商品。可用下方代码生成此表。
| tradeId | goodsLst |
|---|---|
| id001 | A,B,E |
| id002 | A,B,C,E |
| id003 | A,B,C |
| id004 | B,D |
| id005 | B,C |
| id006 | A,B,D |
| id007 | B,C,D |
| id008 | A,C |
| id009 | B,C |
| id0010 | A,C |
data_goods = pd.DataFrame({'tradeId': [f'id00{i}' for i in range(1,11)],
'goodsLst': ['A,B,E', 'A,B,C,E', 'A,B,C', 'B,D', 'B,C', 'A,B,D', 'B,C,D', 'A,C', 'B,C', 'A,C']})
以前述的 A+B=>C 为例,这条规则的支持度 = 同时包含 A, B, C 的订单数 / 订单总数,即 2 / 10 = 0.2 。其置信度 = 同时包含 A, B, C 的订单数 / 同时包含 A, B 的订单数,即 2 / 4 = 0.5。支持度体现了商品(组)的受欢迎程度,置信度体现了商品(组)对另一商品(组)的影响力。在挖掘关联规则时,需指定最小支持度和最小置信度,毕竟不收欢迎的商品,即使它们之间相辅相成,把它们摆在一起也不会有很多人买。
二、频繁项集
为了批量计算所有组合之间的关系,我们需要构建频繁项集,以下为百度百科对频繁项集的定义。
项集:最基本的模式是项集,它是指若干个项的集合。频繁模式是指数据集中频繁出现的项集、序列或子结构。频繁项集是指支持度大于等于最小支持度(min_sup)的集合。
先将原始数据转为集合形式,便于进行运算。
data_goods['goodsSet'] = data_goods['goodsLst'].apply(lambda x: set(x.replace(',', '')))
data_goods

将所有订单的中的商品整合成一个列表,用于对每个商品进行计数,即可生成频繁 1 项集,如商品 A 出现在 6 个订单中。
all_goods = sum(data_goods['goodsLst'].str.split(','), [])
itemset_1 = Counter(list(all_goods)).items()
itemset_1
dict_items([(‘A’, 6), (‘B’, 8), (‘E’, 2), (‘C’, 7), (‘D’, 3)])
计算关联规则需要生成频繁 k 项集(k≤最大组合个数),编写一个 get_item_set() 以便使用。默认最小支持度计数为 2 ,即某商品组至少要出现 2 次。利用 comb() 生成 k 个商品构成的组合,再判断这些组合集是否出现在订单集中。下图为生成的频繁 2 项集,如第一行即表示商品 A+B 出现在 4 个订单中。
def count_grp(s, the_col): # 计算目标集合在集合列中是子集的数量
return the_col.apply(lambda x: 1 if s.issubset(x) else 0).sum()
def get_item_set(uni_lst, the_col, k, min_support=2): # 生成 k 项集
grp_goods = [i for i in comb(uni_lst, k)]
df_itemset = pd.DataFrame({'grp': [set(i) for i in grp_goods]})
df_itemset['count'] = df_itemset['grp'].apply(
lambda x: count_grp(x, the_col))
return df_itemset[df_itemset['count'] >= min_support]
uni_goods = [i[0] for i in itemset_1]
itemset_2 = get_item_set(uni_goods, data_goods['goodsSet'], k=2)
itemset_2
再写一个 get_all_item_set() 用于生成候选总集,我们选择生成至频繁 4 项集(但 4 个商品构成的组合没有在订单中出现 2 次,被过滤)。
def get_all_item_set(uni, the_col, n, min_support=2): # 生成候选总集
all = []
for i in range(1, n+1):
all.append(get_item_set(uni, the_col, k=i, min_support=min_support))
return pd.concat(all)
all_itemset = get_all_item_set(uni_goods, data_goods['goodsSet'], n=4)
all_itemset
三、置信度
前置准备做好了,接下来就可以根据前述公式计算商品(组)间的置信度了。 我们以 A+E=>B 做测试,可见买了商品 A 和 E 时极有可能会买商品 B。
def get_confidence(term, aim, itemsets): # 计算置信度
result = term.union(aim)
support_term = itemsets[itemsets['grp'] == term]['count'].values
support_result = itemsets[itemsets['grp'] == result]['count'].values
support_term = support_term[0] if support_term else 0
support_result = support_result[0] if support_result.size > 0 else 0
confidence = support_result/support_term if support_term > 0 else 0
return f'{term}=>{aim}', confidence
get_confidence({'A', 'E'}, {'B'}, all_itemset)
(“{‘A’, ‘E’}=>{‘B’}”, 1.0)
四、关联规则
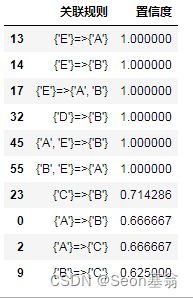
最后计算一下所有的关联规则,传入之前生成的候选总集 all_itemset,默认最小置信度为 0.6。由此,我们得到了所有存在较强关联的商品(组)。
def apriori(itemsets, gro_col='grp', min_confidence=0.6): # 计算所有关联规则并筛选
all_tuple = [i for i in perm(itemsets[gro_col], 2)] # 生成条件=>目标组
all_tuple = [(term, aim) for term, aim in all_tuple if aim.isdisjoint(term)] # 条件和目标无交集
grp_c_lst = []
for term, aim in all_tuple:
grp, c = get_confidence(term, aim, itemsets)) # 逐个计算置信度
grp_c_lst.append((grp, c))
df = pd.DataFrame(data=grp_c_lst, columns=['关联规则', '置信度'])
return df[df['置信度'] > min_confidence].sort_values('置信度', ascending=False)
apriori(all_itemset)
五、小结
本文初步实现了 Apriori 算法,对商品的关联规则进行了探索,如有不足,欢迎大佬们指出改正。这里是再不水文的话下班回家就只想睡觉的 Seon塞翁,下一篇见!
简明使用:三个步骤,整理指定格式数据输入->生成候选项集->计算关联规则。
# 输入唯一商品名列表,所有订单商品集合列,最大项集数
all_itemset = get_all_item_set(uni_goods, data_goods['goodsSet'], n=3)
# 输入候选项集(组合集+频数的形式)
apriori(all_itemset)