目录
适用条件
基本操作函数
功能实现函数
测试使用图
算法讲解
初始化
迭代
贝尔曼福特算法代码
全部代码
实验结果
适用条件
图中可以有负权,但不能有负圈(圈中弧或边的权值之和小于0)
基本操作函数
- InitGraph(Graph &G) 初始化函数 参数:图G 作用:初始化图的顶点表,邻接矩阵等
- InsertNode(Graph &G,VexType v) 插入点函数 参数:图G,顶点v 作用:在图G中插入顶点v,即改变顶点表
- InsertEdge(Graph &G,VexType v,VexType w) 插入弧函数 参数:图G,某弧两端点v和w 作用:在图G两点v,w之间加入弧,即改变邻接矩阵
- Adjancent(Graph G,VexType v,VexType w) 判断是否存在弧(v,w)函数 参数:图G,某弧两端点v和w 作用:判断是否存在弧(v,w)
- BFS(Graph G, int start) 广度遍历函数 参数:图G,开始结点下标start 作用:宽度遍历
- DFS(Graph G, int start) 深度遍历函数(递归形式)参数:图G,开始结点下标start 作用:深度遍历
- Dijkstra(Graph G, int v) 最短路径 - Dijkstra算法 参数:图G、源点v
- Bellman_Ford(Graph G, int v) 最短路径 - Bellman_Ford算法 参数:图G、源点v 作用:计算不含负圈图的最短路径 返回是否有圈
功能实现函数
- CreateGraph(Graph &G) 创建图功能实现函数 参数:图G InsertNode 作用:创建图
- BFSTraverse(Graph G) 广度遍历功能实现函数 参数:图G 作用:宽度遍历
- DFSTraverse(Graph G) 深度遍历功能实现函数 参数:图G 作用:深度遍历
- Shortest_Dijkstra(Graph &G) 调用最短路径-Dijkstra算法 参数:图G、源点v
- Shortest_Bellman_Ford(Graph &G) 调用最短路径- - Bellman_Ford算法 参数:图G
测试使用图
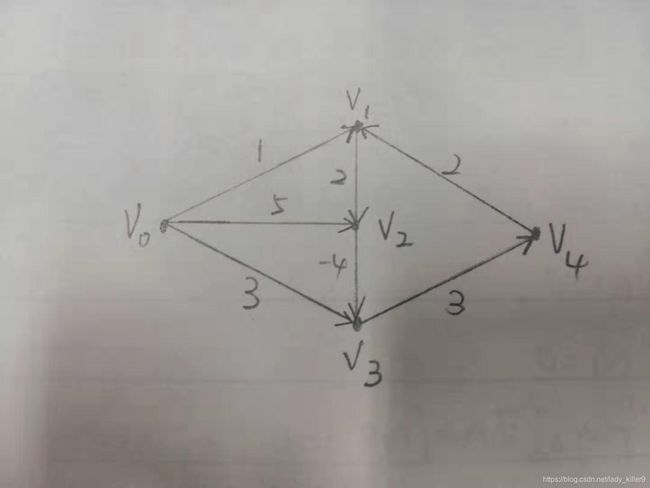
测试用图
算法讲解
| 迭代次数\目标结点 |
v0 |
v1 |
v2 |
v3 |
v4 |
pr |
| 1 |
0 |
1 |
5 |
3 |
∞ |
pr[0]=-1,pr[1]=0 pr[2]=0,pr[3]=0 pr[4]=0 |
| 2 |
0 |
1 |
3 |
1 |
6 |
pr[0]=-1,pr[1]=0 pr[2]=1,pr[3]=2 pr[4]=3 |
| 3 |
0 |
1 |
3 |
-1 |
4 |
pr[0]=-1,pr[1]=0 pr[2]=1,pr[3]=2 pr[4]=3 |
| 4 |
0 |
1 |
3 |
-1 |
2 |
pr[0]=-1,pr[1]=0 pr[2]=1,pr[3]=2 pr[4]=3 |
多说一句,其中一个作者 Richard Bellman是动态规划的创始人,上面的表也就体现了动态规划的思想。下面的迭代部分红色部分就是状态转移方程(博主不喜欢用数学的符号化语言进行描述,一般都是理解了用文字来告诉读者)。
初始化
首次迭代结果,即与源点直连的边的权值,若无直连,则为无穷。
迭代
每次迭代都是与上一次迭代结果相比较。迭代次数即与源点之间的边数。迭代结果即min{上次迭代结果,边数增加后的权值之和}。
第二次迭代,目标节点为v2,从源点出发经过两条边到达v2时,最短路径(v0->v1->v2)长度变为3(1+2)。
目标节点为v3,从源点出发经过两条边到达v3时,最短路径(v0->v2->v3)长度变为1(5-4)。
目标节点为v4,从源点出发经过两条边到达v4时,最短路径(v0->v3->v4)长度变为6(3+3)。
第三次迭代,目标节点为v3,从源点出发经过三条边到达v3时,最短路径(v0->v1->v2->v3)长度变为-1(1+2-4)。
目标节点为v4,从源点出发经过三条边到达v4时,最短路径(v0->v2->v3->v4)长度变为4(5-4+3)。
第四次迭代,目标节点为v4,从源点出发经过四条边到达v4时,最短路径(v0->v1->v2->v3->v4)长度变为2(1+2-4+3)。
pr很简单,每次迭代更新就好,就不讲解了。
贝尔曼福特算法代码
//最短路径 - Bellman_Ford算法 参数:图G、源点v 作用:计算不含负圈图的最短路径 返回是否有圈
bool Bellman_Ford(Graph G, int v)
{
//初始化
int n = G.vexnum;//n为图的顶点个数
for (int i = 0; i < n; i++)
{
D[i] = G.Edge[v][i];
if (D[i] < INF)Pr[i] = v; //v与i连接,v为前驱
else Pr[i] = -1;
}
D[v] = 0;
//初始化结束,开始双重循环
for(int i=2;i D[j] + G.Edge[j][k])
{
D[k] = D[j] + G.Edge[j][k];
Pr[k] = j;
}
//判断是否含有负圈
bool flag = true;
for (int j = 0; j D[j] + G.Edge[j][k])
{
flag = false;
break;
}
return flag;
}
算法自带负圈检测,并且可知道负圈包含的节点。若含有负圈,则包含的点的最短路径值不收敛。
全部代码
/*
Project: 图-最短路径-Bellman-Ford算法(可含有负权弧)
Date: 2019/10/24
Author: Frank Yu
基本操作函数:
InitGraph(Graph &G) 初始化函数 参数:图G 作用:初始化图的顶点表,邻接矩阵等
InsertNode(Graph &G,VexType v) 插入点函数 参数:图G,顶点v 作用:在图G中插入顶点v,即改变顶点表
InsertEdge(Graph &G,VexType v,VexType w) 插入弧函数 参数:图G,某弧两端点v和w 作用:在图G两点v,w之间加入弧,即改变邻接矩阵
Adjancent(Graph G,VexType v,VexType w) 判断是否存在弧(v,w)函数 参数:图G,某弧两端点v和w 作用:判断是否存在弧(v,w)
BFS(Graph G, int start) 广度遍历函数 参数:图G,开始结点下标start 作用:宽度遍历
DFS(Graph G, int start) 深度遍历函数(递归形式)参数:图G,开始结点下标start 作用:深度遍历
Dijkstra(Graph G, int v) 最短路径 - Dijkstra算法 参数:图G、源点v
Bellman_Ford(Graph G, int v) 最短路径 - Bellman_Ford算法 参数:图G、源点v 作用:计算不含负圈图的最短路径 返回是否有圈
功能实现函数:
CreateGraph(Graph &G) 创建图功能实现函数 参数:图G InsertNode 作用:创建图
BFSTraverse(Graph G) 广度遍历功能实现函数 参数:图G 作用:宽度遍历
DFSTraverse(Graph G) 深度遍历功能实现函数 参数:图G 作用:深度遍历
Shortest_Dijkstra(Graph &G) 调用最短路径-Dijkstra算法 参数:图G、源点v
Shortest_Bellman_Ford(Graph &G) 调用最短路径- - Bellman_Ford算法 参数:图G
*/
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
实验结果
最短路径与生成树

最短路径(红笔)与生成树
实验结果截图

结果截图
更多数据结构与算法实现:数据结构(严蔚敏版)与算法的实现(含全部代码)
有问题请下方评论,转载请注明出处,并附有原文链接,谢谢!如有侵权,请及时联系。


