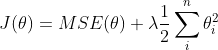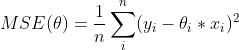【机器学习入门】(8) 线性回归算法：正则化、岭回归、实例应用(房价预测)附python完整代码和数据集
各位同学好，今天我和大家分享一下python机器学习中线性回归算法的实例应用，并介绍正则化、岭回归方法。在上一篇文章中我介绍了线性回归算法的原理及推导过程：【机器学习】(7) 线性回归算法：原理、公式推导、损失函数、似然函数、梯度下降
本节中我将借助Sklearn库完成波士顿房价预测，带大家进一步学习线性回归算法。文末附python完整代码。那我们开始吧。
1. Sklearn 库实现
1.1 线性回归方法选择
（1）正规方程的线性回归
导入方法： from sklearn.linear_model import LinearRegression
当数据量较小时(<10万条)，使用该方法的准确率更高
（2）梯度下降法
导入方法： from sklearn.linear_model import SGDClassifier
当数据集很大时，使用该方法准确率更高。(尽量采用岭回归方法，得到的结果会更好)
梯度下降法公式我已经在上一篇文章中推导过，正规化方程的推导本文不做介绍，感兴趣的可自己查阅一下资料。正则化岭回归方法在文末介绍。
1.2 模型准确率的评分方法
（1）平均误差
导入方法： from sklearn.metrics import mean_absolute_error
计算平均误差方法： mean_absolute_error( 真实值 , 预测值 )
（2）均方误差
导入方法： from sklearn.metrics import mean_squared_error
计算均方误差： mean_squared_error( 真实值 , 预测值 )
2. 实例应用 -- 房价预测
2.1 数据获取
波士顿房价数据时sklearn中自带的数据，可以直接调用。如果有同学对sklearn内部数据集获取有疑问的话，可以参考我的前几篇文章，如下文的第2.1小节：【机器学习】(1) K近邻算法：原理、实例应用（红酒分类预测）附python完整代码及数据集
#（1）数据获取
from sklearn.datasets import load_boston
boston = load_boston() #保存波士顿房价数据集
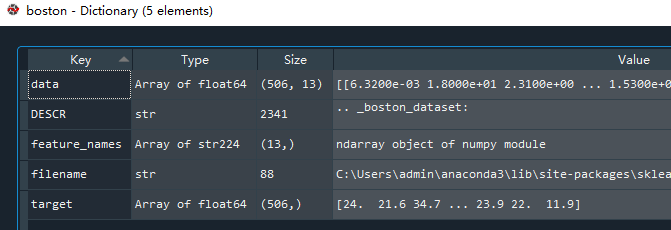
读取数据集的返回值是一个.Bunch类型数据，含有13项特征值，1项房价目标值。data中存放的是特征值数据，DESCR是对该数据集的描述，feature_names是特征值的名称，filename是该数据集的路径，target是房价数据。
2.2 数据处理
从.Bunch数据中获取特征值和目标值数据，boston_features存放的是影响房价的13项特征数据，boston_targets存放的是房价。
由于线性规划对特征值比较敏感，数据对预测结果的影响也比较大。为了避免数据单位不统一以及数据跨度较大等问题导致预测结果不准确，因此对特征值数据进行标准化处理。
标准化方法导入： from sklearn.preprocessing import StandardScaler
转换方法： scaler.fit_transform()
#（2）数据处理
# 获取特征值
boston_features = boston.data
# 获取目标值
boston_targets = boston.target
# 标准化处理--正态分布
from sklearn.preprocessing import StandardScaler #导入标准化处理方法
scaler = StandardScaler() #接收标准化方法
# 将特征值数据传入标准化转换函数中
boston_features = scaler.fit_transform(boston_features)
2.3 划分训练集和测试集
一般采用75%的数据用于训练，25%用于测试，因此在数据进行预测之前，先要对数据划分。
#（3）划分训练集和测试集
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(boston_features,boston_targets,test_size=0.25)
如果有同学对测试集和训练集划分方法有疑问的可以看下文的第3.1小节：【机器学习】(1) K近邻算法：原理、实例应用（红酒分类预测）附python完整代码及数据集_小狄同学的博客-CSDN博客
2.4 使用正规方程方法预测
使用linear接收正规方程方法，训练函数 .fit() 中传入训练值，预测函数 .predict() 传入测试集的特征值x_test，而测试集的目标值y_test用来计算模型误差。
# 导入正规方程方法
from sklearn.linear_model import LinearRegression
# linear接收正规化方法
linear = LinearRegression()
# 训练，输入训练所需的特征值和目标值
linear.fit(x_train,y_train)
# 预测，输入预测所需的特征值
linear_predict = linear.predict(x_test)
计算模型误差
分别计算房价预测值 linear_predict 和真实值 y_test 之间的平均误差和均方误差，得到模型的平均误差为3.5，均方误差为21.2
# 使用平均误差计算模型准确率
from sklearn.metrics import mean_absolute_error
# 传入预测结果和真是结果计算平均误差
linear_mean_absolute = mean_absolute_error(y_test,linear_predict)
# 使用均方误差计算模型准确率
from sklearn.metrics import mean_squared_error
# 传入预测结果和真是结果计算均方误差
linear_mean_squared = mean_squared_error(y_test,linear_predict)
2.5 使用梯度下降法预测
与上述方法同理，sgd存放梯度下降方法，训练函数.fit()中传入训练所需的特征值和目标值，预测函数.predict()中传入预测所需的特征值x_test。
！注意！：在sklearn 模型训练如果出现如下报错：‘ValueError: Unknown label type: ‘unknown’’
这时在训练所需的目标值后面加上 .astpye('str') 或 astype('int') 即可
如果训练的目标值y_train是整型数据，写成 fit(x_train,y_train.astype('int'))
如果训练的目标值y_train是浮点型数据，写成 fit(x_train,y_train.astype('str'))
#（5）使用梯度下降法预测
# 导入梯度下降法方法
from sklearn.linear_model import SGDClassifier
# sgd接收梯度下降方法
sgd = SGDClassifier()
# 训练
sgd.fit(x_train,y_train.astype('str'))
# 预测
sgd_predict = sgd.predict(x_test)
# 使用平均误差计算准确率
sgd_mean_absolute = mean_absolute_error(y_test,sgd_predict)
# 使用均方误差计算准确率
sgd_mean_squared = mean_squared_error(y_test,sgd_predict)
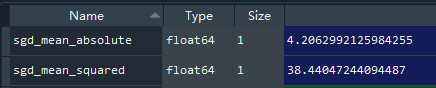
分别计算房价预测值 sgd_predict 和真实值 y_test 之间的平均误差和均方误差，得到模型的平均误差为4.2，均方误差为38.4
由此可见，在数据量较少的情况下，正规方程线性回归比梯度下降线性回归的准确率要稍微高一些
3. 正则化与岭回归
正则化(规整化)出现的目标是为了防止过拟合现象，公式如下：
在上一节中我们证明了推导了损失函数 
的公式由来，MSE(
)也可以理解为损失函数。只有除的常数项不一样，其他都一样，如下式：
， 
此外，式中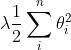 
表示正则化，那么正则化的作用是什么呢，我举个例子帮助大家理解。
假设现在有一组特征值x=[1,1,1,1]，若在进行线性回归的时候，权重 可以取两组值，
=[1,0,0,0]，
=[0.25,0.25,0.25,0.25]，权重 和 与 x 相乘的结果相同。那我们究竟选那一组权重比较好呢， 这时带入正则化方法， 正则化之后的结果为 
， 正则化之后的结果为 
，选择正则化最小的这一组参数，因此我们选择 这组参数。因为正则化结果越小，对应的权重越小，对模型越有利。若某一个特征权重很大，那么稍微一点点的变化都会对模型产生很大影响。
回到公式中，
代表惩罚力度， 越大，正则化越大，而我们选择正则化后结果最小的那组参数。因此 越大，说明惩罚力度越大。但惩罚力度并不是越大越好，太大了，可能会导致模型处理拟合得不好，导致最终预测评分低。 需要不断调试。
岭回归，就是加入了正则惩罚项的回归，可用 sklearn.linear_model.Ridge 来实现。
from sklearn.linear_model import Ridge
ridge = Ridge( alpha = 1 )
此处的 alpha 代表惩罚力度
我们使用岭回归方法再对这个例子进行预测
#（6）使用岭回归预测
# 导入岭回归方法
from sklearn.linear_model import Ridge
# 接收岭回归方法，自定义惩罚力度
ridge = Ridge(alpha=10)
# 训练
ridge.fit(x_train,y_train)
# 预测
ridge_predict = ridge.predict(x_test)
# 误差计算
# 平均误差
ridge_mean_absolute = mean_absolute_error(y_test, ridge_predict)
# 均方误差
ridge_mean_squared = mean_squared_error(y_test,ridge_predict)
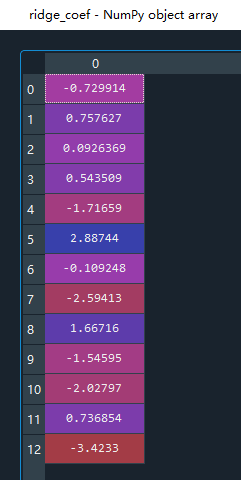
# 输出每一项的权重
ridge_coef = ridge.coef_
# 输出偏移量
ridge_intercept = ridge.intercept_
得到房价预测值和真实值的平均误差为3.2，均方误差为20.4
查看每一项的权重值： ridge.coef_
查看偏移量
的值： ridge.intercept_
即线性回归公式中： 
完整代码展示：
#（1）数据获取
from sklearn.datasets import load_boston
boston = load_boston() #保存波士顿房价数据集
#（2）数据处理
# 获取特征值
boston_features = boston.data
# 获取目标值
boston_targets = boston.target
# 线性回归对特征值比较敏感，数据对结果的影响比较大，如果有某一项过大，会产生很大影响
# 标准化处理--正态分布
from sklearn.preprocessing import StandardScaler #导入标准化处理方法
scaler = StandardScaler() #接收标准化方法
# 将特征值数据传入标准化转换函数中
boston_features = scaler.fit_transform(boston_features)
#（3）划分训练集和测试集
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(boston_features,boston_targets,test_size=0.25)
#（4）使用正规方程预测
# 导入正规方程方法
from sklearn.linear_model import LinearRegression
# linear接收正规化方法
linear = LinearRegression()
# 训练，输入训练所需的特征值和目标值
linear.fit(x_train,y_train)
# 预测，输入预测所需的特征值
linear_predict = linear.predict(x_test)
# 使用平均误差计算模型准确率
from sklearn.metrics import mean_absolute_error
# 传入预测结果和真是结果计算平均误差
linear_mean_absolute = mean_absolute_error(y_test,linear_predict)
# 使用均方误差计算模型准确率
from sklearn.metrics import mean_squared_error
# 传入预测结果和真是结果计算均方误差
linear_mean_squared = mean_squared_error(y_test,linear_predict)
#（5）使用梯度下降法预测
# 导入梯度下降法方法
from sklearn.linear_model import SGDClassifier
# sgd接收梯度下降方法
sgd = SGDClassifier()
# 训练
sgd.fit(x_train,y_train.astype('str'))
# 预测
sgd_predict = sgd.predict(x_test)
# 使用平均误差计算准确率
sgd_mean_absolute = mean_absolute_error(y_test,sgd_predict)
# 使用均方误差计算准确率
sgd_mean_squared = mean_squared_error(y_test,sgd_predict)
#（6）使用岭回归预测
# 导入岭回归方法
from sklearn.linear_model import Ridge
# 接收岭回归方法
ridge = Ridge(alpha=10)
# 训练
ridge.fit(x_train,y_train)
# 预测
ridge_predict = ridge.predict(x_test)
# 误差计算
# 平均误差
ridge_mean_absolute = mean_absolute_error(y_test, ridge_predict)
# 均方误差
ridge_mean_squared = mean_squared_error(y_test,ridge_predict)
# 输出每一项的权重
ridge_coef = ridge.coef_
# 输出偏移量
ridge_intercept = ridge.intercept_