【论文笔记】Deep Learning with Differential Privacy

原文：Deep Learning with Differential Privacy
PPT：https://qdata.github.io/deep2Read//talks/20171012-Bargav-2.pdf
参考：https://my.oschina.net/u/4296470/blog/3275849
初学DP，原文 Section 1-4 部分，仅为记录。

INTRODUCTION

深度学习+差分隐私
在差分隐私的框架内对隐私成本进行重新定义和分析
对先前工作（在参数少的凸模型上 or 处理复杂神经网络时（ with 隐私损失大）有很好结果）的改进：非凸目标，几层（实际上只有1-2隐藏层），百万参数，隐私成本的重定义。
本文工作：

1. 跟踪隐私损失详细信息（高阶矩），获得更严格的估计
2. 提高差分隐私的计算效率：单个训练示例的梯度计算算法（单个训练示例？？），细分任务为更小批次（减少内存占用），在输入层应用差分隐私主投影（PCA？）。
3. 在 tensorflow 上训练具有差分隐私的模型。在2个分类任务上评估该方法。

实际上，我觉得本文最主要的贡献还是 privacy accounting 上，主要是moments accountant 方法的提出，我个人认为这篇文章看这一部分就足够了，但是这部分感觉不太好懂。

Differentially Private SGD Algorithm

这个很好理解，就是在普通SGD上增加了一步Add noise操作。Clip gradient也是常见的解决梯度爆炸的技术，也就是 || g(xi) || > C 时候，g(xi) = C · g(xi) / || g(xi) ||。

The Moments Accountant

Moments Accountant 跟踪隐私损失随机变量的矩的界限。它推广了跟踪 (ε，δ) 的标准方法，并使用了 strong composition theorem。虽然这种改进以前用于组合高斯机制，但是我们表明它也适用于用随机采样的合成高斯机制，并且可以提供更严格隐私损失估计。{ moments accountant 不是作者原创的吗？为什么说以前用于组合高斯机制？}

机制 M (ε, δ) 等价于M的隐私损失随机变量上的某个尾部边界。尾部边界是分布中非常有用的信息，直接从尾部组合会导致非常宽松的边界。

计算隐私损失变量的对数矩，利用矩界+马尔科夫不等式—>尾界

隐私损失定义：

通过顺序（线性？）应用差分隐私机制来更新状态。这是自适应合成的一个例子，通过让 kth 机制 Mk 的辅助输入作为先前所有机制的输出来建模。{ 也就是说文章的隐私损失相比传统定义，多了一个辅助输入aux，而aux是M1，M2，······，Mk-1的输出 }
对于机制 M，我们定义了 λth 矩 αM (λ; aux, d, d`) 作为在值 λ 处评估的矩母函数的对数：{ 也就是说 αM 是 c 的矩母函数的对数 }

矩母函数：

为了证明一个机制的隐私保证，限制所有可能的 αM 是有用的。最大值接管所有可能的 aux 辅助性输入和所有相邻数据库d，d’ 。

α 的性质：
1）组合性：假设一个机制 M 由一系列自适应机制 M1······Mk 组成，

（R1 x R2 x ······x Ri-1 x D—>Ri ?? ）对于任意 λ ，

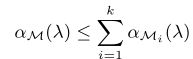
2）尾部界限：对于任何 ε > 0，机制 M 是 (ε，δ) -差分隐私的：

△ △ 根据性质1，在每一步计算、约束 αMi (λ)。将它们相加，约束该机制 M （M由M1，M2，······，Mk组成）的整体力矩。再根据性质2，计算δ。
下面的内容不太懂，不是要计算 αMi (λ) 吗，怎么之后在讲计算 α(λ) ？两者的关系是什么？

Hyperparameter Tuning

与神经网络的结构相比，模型的精度对批处理大小和噪声等级等训练参数更敏感。
如果尝试对超参数做一些设置，我们或许可以通过 moments accountant 简单地累加合计所有设置的隐私成本。然而，我们只关心给我们提供最准确的模型的设置，这可以让我们可以做得更好，例如应用Gupta等人的结果版本。
我们可以使用理论上的见解来减少需要尝试的超参数设置的数量。

batch 凸目标函数的差分隐私优化最好使用1的 batch ，非凸学习不太稳定，需要聚合到更大的 batch 。batch 太大会增加隐私成本，所以我们将每个 epoch 的批次数量与 epoch 所需数量的顺序相同？？？

学习率 当模型收敛到局部最优时，非隐私训练的学习率会适当向下调整。而差分隐私训练不需要将学习率调至过小，因为它永远不会达到合理的制度。所以从相对较大的学习率开始，然后在几个时期内线性衰减到较小的值，然后保持不变。

Implementation

在tensorflow上实现差分隐私SGD。

1. sanitizer：对梯度预处理以保护隐私
2. privacy_accountant：跟踪训练过程中的隐私支出

DPSGD_Optimizer 最小化损失函数；
DPTrain 迭代调用 DPSGD_Optimizer，使用隐私accountant 限制总隐私损失。

sanitizer
1）通过剪切每个示例的梯度范数来限制每个示例的灵敏度（怎么就限制敏感度了呢？不太懂）；
2）在更新网络参数之前向一个 batch 的梯度添加噪声（不是向lot？）。
per_example_gradient操作符，不明白作者后面在说什么？

Privacy accountant
实现了moments accountant，在每一步中额外地累积了隐私损失矩的对数。
根据噪声分布，计算 α(λ)，要么通过应用一个渐进界，要么评估一个封闭式的表达式，要么通过应用数值积分。第一种选择是恢复一般的高级组成定理，后两种给出更准确地隐私损失计算。之前提到用数值积分计算 α(λ)，这小节说用数值积分计算E1、E2，α(λ) 根据E1、E2定义。在 λ 的范围内计算 α(λ)，并使用定理2.2（尾界）可计算最好的 (ε, δ)。对于我们感兴趣的参数来说，计算 λ<=32 的 α(λ) 就足够了。
在训练过程的任何时候，都可以使用定理2.2查询隐私损失。罗杰斯等人指出了与自适应选择隐私参数相关的风险。我们通过提前确定迭代次数和隐私参数，避免他们的攻击和负面结果。隐私计算的更一般实现必须正确区分两种操作模式——作为隐私里程表（距离？）或隐私过滤器。

Differentially private PCA
主成分分析是获取输入数据主要特征的一种有用的方法。差分隐私PCA算法，从训练样本随机抽取一例作为向量，并将每个向量归一化为单位 l2 范数，形成矩阵A，其中每个向量是矩阵中的一行。然后添加高斯噪音到协方差矩阵Aτ A中，计算噪声协方差矩阵的主要方向。对于每个输入样本，将投影应用到主要方向上，再输入到神经网络。

归一化每个抽取到的示例形成A->添加高斯噪声到ATA->计算主要方向->投影->输入到神经网络

运行PCA产生了隐私成本，但是提升了模型的质量并减少了运行时间。

Convolutional layers
在 tensorflow 中，卷积层的一个高效的per-example梯度计算仍然是一个挑战。
探索在公共数据上学习卷积层的想法。
{才疏学浅，仍然不知道在说什么。}