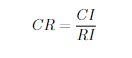人类量化思维之光——层次分析法

---

联系数计加油站获取论文和代码等资源。
邮箱: [email protected]
微信公众号:数计加油站
致谢:清风数学建模

---

评价是什么?

评价是什么?这个问题很简单。评价就是回答两个问题:一个东西好不好?它好的程度是多少?

评价是为了作出选择。生活中，我们无时无刻不在进行着评价和选择: 手机应该买哪个牌子的呢，哪个牌子好一点呢?应该学什么专业呢，什么专业比较有前景呢？学习哪门编程语言呢，哪门编程语言学得更有价值呢?手机挑选问题、专业报考问题、语言比较问题，都是评价问题。

怎么评价呢?生活经验告诉我们，为了挑选出最好的手机牌子，我们要比较各个品牌的手机的各方面:价格、性能、颜值……；为了报考最适合自己的专业，我们要比较各个专业的各方面:男女比例、专业前景、兴趣匹配度……；为了得出学得最有意义的编程语言，我们要比较各门语言的各方面: 难易程度、使用度、社区活跃度……也就是说，评价建立在比较某些指标的基础之上。

用一句话概述:评价就是通过比较某些指标的好坏，得出评价对象的好坏，从而作出某种选择。

层级思想:不着急，一个一个来

层次分析法是什么呢?层次分析法就是划分层次来分析的方法。

没错，就是分层。为什么要分层呢?原因有很多:

1. 有时候我们的评价指标会非常多，而且指标之间还会有各种各样的包含关系。分层有利于我们直观地了解这些复杂关系。

2. 分层其实是我们大脑思维的潜意识处理方式。

3. 分层有利于理清计算过程(后面会提到)。

最简单的评价问题层次结构只有三层:目标层、准则层、方案层。它们分别对应上面提到的评价定义中的选择、指标、评价对象。

下面我们展示一个常见的层次结构模型图。它就由三层组成。目标层就是评价的目标:选择最适合小明的旅游景点。方案层就是可供选择的3个旅游景点:苏杭、北戴河、桂林。准则层就是用来评价各个旅游景点好坏的5个指标:景色、花费、居住、饮食、交通。

层次分析法的主体步骤，其实就包含在这张层次结构模型图之中了。我们从下到上，先比一下方案层各个方案对于准则层各个指标的好坏程度，再比一下准则层各个指标对于目标层的重要性程度，最后综合起来，就可以得到方案层各个方案对于目标层的好坏程度。这也就解决了整个的评价问题。

量化思维:打分?打分。打分！

学习情况的好坏怎么得出?你的老师表示:来考个试，我给你打个分就行了。

量化一直是展现好坏程度的不二手段。通过打分，我们能准确地得出一个东西是好还是坏。

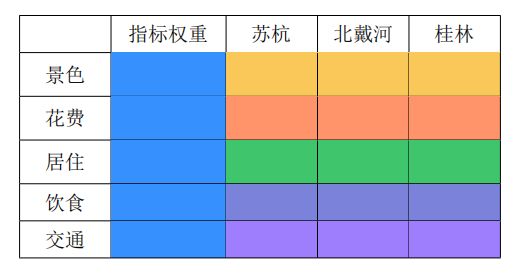
上面提到的好坏程度、重要性程度，都可以用数字来量化描述。对于同一个对象，多个事物的好坏程度或重要性程度，通常用0-1之间的数字来表示，称为这多个事物相对于公共对象的权重。权重之和为1。基于权重，我们可以把上面的层次结构模型图转化为一张表格:

6种颜色，对应6组权重:5个指标相对于目标层的重要性权重。3个景点分别相对于5个指标的好坏权重。第2列分别与第3,4,5列相乘，就可以得到最后的结果权重，也就是3个景点的打分。

通过上面的分析，我们发现，我们评价的目标，就变成了打6组分，再把这6组分归一化成权重。

分治策略:化多为二

分怎么打呢?和老师一样，直接一下就把所有人的分打好？这通常是不现实而且不科学的。因为，在大部分场景下，我们没有考试成绩这样的数据，如果直接一股脑地打好所有的分，通常会顾此失彼，造成“不公平”,“极其不客观”的结果。

仔细思考一下，打分的实质是什么?是用数字量化各个打分对象的绝对好坏、重要程度。绝对，那我可不可以由相对来推导出绝对呢?答案是肯定的。

层次分析法的精髓之一，就是通过两两判断来得出相对得分，最后通过相对得分来计算出绝对得分。

满足上述条件的判断矩阵称为一致性矩阵。容易看出，一致性矩阵的特征值只有1个，而且刚好是方阵的维数n（各行成比例且）。判断矩阵为一致性矩阵的对象的打分，可以直接由判断矩阵各列相加得到。

事实上，我们得出的判断矩阵往往不是一致性矩阵（如果是，那就很好了），但其实只要我们的判断矩阵和一致性矩阵比较接近就可以。检验这个接近性程度的过程就是所谓的一致性检验。

根据前人的研究，可以通过CI,RI,CR三个指标来判断矩阵的一致性程度。

层次分析法的步骤

层次分析法的步骤是:

1. 建立层次结构模型

2. 构造两两判断矩阵

3. 一致性检验

4. 权重计算

5. 计算最终打分

一篇简单的论文

Python代码

初始化

import numpy as np
import matplotlib.pyplot as plt

np.set_printoptions(precision=4)
import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False # 解决图像中的“-”负号的乱码问题

C1 = np.array([[1, 2, 5], [1 / 2, 1, 2], [1 / 5, 1 / 2, 1]])
C2 = np.array([[1, 1 / 3, 1 / 8], [3, 1, 1 / 3], [8, 3, 1]])
C3 = np.array([[1, 1, 3], [1, 1, 3], [1 / 3, 1 / 3, 1]])
C4 = np.array([[1, 3, 4], [1 / 3, 1, 1], [1 / 4, 1, 1]])
C5 = np.array([[1, 1, 1 / 4], [1, 1, 1 / 4], [4, 4, 1]])
print(C1,C2,C3,C4,C5,sep="\n\n")

O = np.array([[1, 1 / 2, 4, 3, 3], [2, 1, 7, 5, 5],
          [1 / 4, 1 / 7, 1, 1 / 2, 1 / 3], [1 / 3, 1 / 5, 2, 1, 1],
          [1 / 3, 1 / 5, 3, 1, 1]])
print(O)

AHPConsistencyCheck函数

def AHPConsistencyCheck(A):
"""对判断矩阵进行一致性检验并计算权重"""

    A = A.copy()
    ## 判断是否非方阵
    m, n = A.shape
    if m != n:
        print(f"判断矩阵应为方阵。但输入矩阵为({m},{n})")
        return False, None, None, None, None

    ## 一致性检验
    # 计算特征向量和特征值
    Lambdas, X = np.linalg.eig(A)
    LambdaIndex = np.argmax(Lambdas)
    Lambda, x = np.real(Lambdas[LambdaIndex]), np.real(X[:, LambdaIndex])

    # 计算CI，RI，CR
    CI = (Lambda - n) / (n - 1)
    RITable = [
        0, 0, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41, 1.46, 1.49, 1.52, 1.54, 1.56,
        1.58
    ]
    RI = RITable[n - 1]
    CR = CI / RI

    # 判断是否通过一致性检验
    if CR >= 0.1:
        return False, None, CI, RI, CR
    else:
        Pass = True

    ## 算术平均法
    # 各列归一化
    for i in range(n):
        A[:, i] = A[:, i] / np.sum(A[:, i])
    # 各列求算术平均
    origin_weights = np.sum(A, 1).reshape((-1, 1))
    weights = origin_weights / sum(origin_weights)

    ## 几何平均法
    # 各列求几何平均
    origin_weights = np.prod(A, 1)
    origin_weights = origin_weights.reshape((-1, 1))
    origin_weights = origin_weights**(1 / n)
    weights = np.concatenate([weights, origin_weights / sum(origin_weights)],
                            1)

    ## 特征值法
    weights = np.concatenate([weights, x.reshape(-1, 1) / np.sum(x)], 1)

    ## 平均值
    weights = np.concatenate(
        [weights, np.sum(weights, 1).reshape(-1, 1) / 3], 1)
    return Pass, weights, CI, RI, CR

sortWeights函数

def sortWeights(weights, labels):
"""从小到大排序权重和标签"""

    weights = weights / sum(weights)
    wl = list(zip(weights, labels))
    wl.sort(key=lambda x: x[0])
    sortedWeights, sortedLabels = zip(*wl)
    sortedWeights = np.array(sortedWeights)
    sortedLabels = list(sortedLabels)
    return sortedWeights, sortedLabels

drawWeights函数

def drawWeights(weights, labels):
"""绘制权重图"""
    n = len(weights)
    ax=plt.axes()
    ax.set_facecolor("#FAFAF8")
    ax.barh([i for i in range(1,
                               len(weights) + 1)],
             weights,
             height=0.2,
             color="#3691ff")
    y = [i for i in range(1, n + 1)]
    plt.yticks(y, labels)
    plt.xlim(0, 1)
    for i in range(n):
        plt.text(weights[i] + 0.01, y[i] - 0.03, weights[i])

AHP主体

Mats = [O, C1, C2, C3, C4, C5]

# 一致性检验
Weights = []
for i in range(len(Mats)):
    Pass, weights, CI, RI, CR = AHPConsistencyCheck(Mats[i])
    Weights.append(weights)
    if Pass:
        print(f"第{i+1}个矩阵通过一致性检验")
        print(f"CI={CI:.6f}  RI={RI:.2f}  CR={CR:.6f}<0.1")
        print(f"权重表为:\n{weights}\n")
    else:
        print(f"第{i+1}个矩阵未通过一致性检验!!!")
        print(f"CI={CI:.6f}  RI={RI:.2f}  CR={CR:.6f}>=0.1\n")

# 权重汇总表
weightsTable = np.ones(shape=(5, 4))
weightsTable[:, 0] = Weights[0][:, -1]
for i in range(1, len(Mats)):
    weightsTable[i - 1, 1:] = Weights[i][:, -1]
print(f"权重汇总表:\n{weightsTable}\n")

# 最终打分计算
grades = np.ones(3)

for i in range(3):
    grades[i] = np.dot(weightsTable[:, 0].T, weightsTable[:, i + 1])
print(f"最终得分:\n{grades}\n")

# 可视化
sortedWeights,sortedLabels = sortWeights(grades,["苏杭","北戴河","杭州"])
drawWeights(np.round(sortedWeights,4),sortedLabels)        

Matlab代码

AHPConsistencyCheck.m

function [pass,weights,CI,RI,CR] = AHPConsistencyCheck(A)
% 层次分析法(AHP)中对判断矩阵A进行一致性检验并计算权重
% [pass,weights,CI,RI,CR] = AHPConsistencyCheck(A)
% pass=true表示通过一致性检验,pass=false则为未通过
% weights:返回的权重矩阵。
% 从左到右各列分别为算术平均法、几何平均法、特征值法、平均值
% CI,RI,CR:相关检验量
% A:判断矩阵
        
    %% 判断矩阵是否为方阵
    [m,n] = size(A); 
    if m ~= n
        disp("判断矩阵应为方阵,但输入为(" + num2str(m) + "," ...
            + num2str(n) + ")");
    end

    %% 一致性检验
    [X,Lambda]=eig(A);  % 求特征值和特征向量

    % 寻找最大特征值及对应的特征向量
    lambda = Lambda(1,1);
    indexOFlambda = 1;
    for i=2:n
        if Lambda(i,i) > lambda
            lambda = Lambda(i,i);
            indexOFlambda = i;
        end
    end
    x = X(:,indexOFlambda);
    
    % 计算CI,查询RI,计算CR
    CI = (lambda - n)/(n - 1);
    RItable = [0,0,0.52,0.89,1.12,1.26,1.36,1.41,1.46,...
        1.49,1.52,1.54,1.56,1.58];
    RI=RItable(n);
    CR = CI/RI;
    
    % 判断是否通过一致性检验
    if CR >= 0.1
        pass = false;
        weights = [];
        return 
    else
        pass = true;
    end

    %% 算术平均法
    % 各列归一化
    for i=1:n
        A(:,i) = A(:,i) / sum(A(:,i));
    end
    % 各列求算术平均
    origin_weight = sum(A,2);
    weights = origin_weight / sum(origin_weight);

    %% 几何平均法
    % 各列求几何平均
    origin_weight = A(:,1);
    for i=2:n
        origin_weight = origin_weight .* A(:,i);
    end
    origin_weight = origin_weight.^(1/n);
    % 结果向量归一化
    weights = [ weights , origin_weight / sum(origin_weight)];
    
    %% 特征值法
    origin_weight = x;
    weights = [ weights , origin_weight / sum(origin_weight)];
    
    %% 平均值
    weights = [ weights , sum(weights,2) / 3];
end

drawWeights.m

function  drawWeights(weights,labels)
% 绘制权重图
% weights:权重行向量或列向量
% labels:数据标签

    n = length(weights);
    weights = weights / sum(weights);
    facecolor = "#3691ff";
    width = 0.3;
    barh(weights,FaceColor=facecolor,BarWidth=width);
    xlim([0,3/2*max(weights)]);
    yticks(1:n)
    yticklabels(labels);
    for i=1:n
        text(weights(i)+1/100*max(weights),i,num2str(weights(i)))
    end

end

main.m

% 通过层次分析法选择最佳旅游地

clear,clc

%% 输入判断矩阵

% 准则层对目标层
O = [1 1/2 4 3 3
    2 1 7 5 5
    1/4 1/7 1 1/2 1/3
    1/3 1/5 2 1 1
    1/3 1/5 3 1 1];

% 方案层对准则层
C1 = [1 2 5; 1/2 1 2; 1/5 1/2 1];
C2 = [1 1/3 1/8; 3 1 1/3; 8 3 1];
C3 = [1 1 3; 1 1 3; 1/3 1/3 1];
C4 = [1 3 4; 1/3 1 1; 1/4 1 1];
C5 = [1 1 1/4; 1 1 1/4; 4 4 1];

Mats = {O,C1,C2,C3,C4,C5};
MatNum = size(Mats,2);
Weights = cell(1,MatNum);

%% 一致性检验及权重计算
for i=1:MatNum
    [pass,weights,CI,RI,CR] = AHPConsistencyCheck(Mats{i});
    Weights{i} = weights;
    if pass
        disp("第" + num2str(i) + "个矩阵通过一致性检验");
        disp("CI=" + num2str(CI) + "  RI=" + num2str(RI) ...
            + "  CR=" + num2str(CR) + "<0.1");
        disp("权重表为:");
        disp(weights);
    else
        disp("第" + num2str(i) + "个矩阵未通过一致性检验");
        disp("CI=" + num2str(CI) + "  RI=" + num2str(RI) ...
            + "CR=" + num2str(CR) + ">=0.1");
    end
end

%% 权重汇总表
weightsTable = ones(5,4);
weightsTable(:,1) = Weights{1,1}(:,end);
for i=2:MatNum
    weightsTable(i-1,2:end) = Weights{1,i}(:,end);
end
disp("权重汇总表:");
disp(weightsTable);

%% 计算最终打分
grades = ones(3,1);
for i=1:3
    grades(i,1) = weightsTable(:,1)' * weightsTable(:,i+1);
end
disp("最终得分:");
disp(grades);

%% 可视化
[sortedGrades,sortedLabels] = sortWeights(grades,["苏杭","北戴河","桂林"]);
drawWeights(sortedGrades,sortedLabels);

clear O C1 C2 C3 C4 C5 pass CI RI CR weights i MatNum