零知识证明
交互式证明系统由两方参与,分别为证明者(Prover)和验证者 (Verifier)。证明者掌握某一秘密,证明者需要让验证者相信自己掌握该秘密。
交互式证明过程需要多轮,最典型的是每一轮验证者向证明者发送一个询问信息(挑战,Challenge),证明者对询问信息进行计算,并回复信息响应(Response)。
验证者根据证明者每一轮的回复信息决定是否相信证明者。在交互式证明系统中,通信信道是必须的。交互式证明系统满足:
完备性:如果证明者知道某一秘密,验证者将接受证明的证明。
可靠性:如果证明者能以一定的概率使验证者相信证明者的证明,则证明者知道相应的秘密。
零知识证明(Zero-Knowledge Proof),是指证明者在不让验证者掌握秘密信息的前提下,使得验证者确信自己确实掌握了这些信息。验证者除了知道证明者能证明某一事实外,不能得到其他任何信息。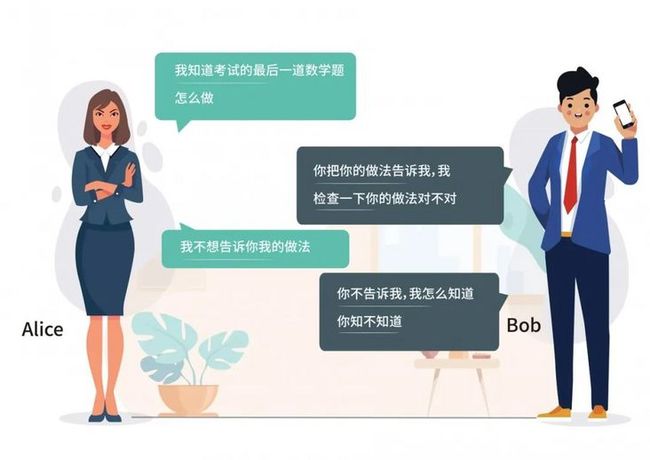
例如,Alice宣称知道一个能够对抛硬币正反面的诀窍。Bob要验证Alice的宣称,只需要当着Alice的面抛硬币。
Bob抛一次硬币Alice能猜中结果的概率为1/2,连续抛两次硬币Alice都能猜中结果的概率为1/4,连续抛次硬币Alice都能猜中结果的概率为1/\( 2^ \),当足够大时,就可以认为Alice全都正确猜中是不可能事件。
那么如果Alice真的全都猜对了,Bob就可以相信Alice的宣称。
另一个经典的例子是有一个简单的迷宫: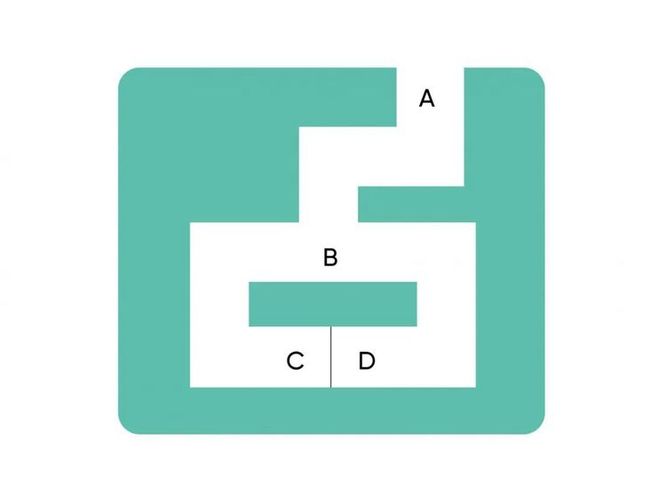
C和D之间有一扇需要秘密口令才能打开的门,证明者要向验证者证明自己能够打开这扇门,又不想泄露秘密口令。可以采用如下所述的证明协议:
1. 验证者在协议开始时停留在位置 A
2. 证明者一直走到迷宫内部的位置 C 或者位置 D 处
3. 在证明者消失之后,验证者走到位置 B 处,然后命令证明者从某个出口处出来
4. 证明者根据验证者的命令,从对应出口处出来
5. 证明者和验证者重复以上过程轮
只有证明者知道口令,每次验证者要求证明者从指定路口出来时,证明者才能根据命令打开门穿过去或者原路返回,从指定路口出来。
如果证明者不知道打开门的秘密口令,则证明者只能原路返回。因此不知道口令的证明者只能在一开始猜测验证者要求的路口,并从该路口进入,一轮猜对的概率是1/2,重复轮后,证明者都能猜对概率为1/\( 2^ \),重复的轮数足够多时,验证者就可相信证明者拥有打开门的秘密口令。
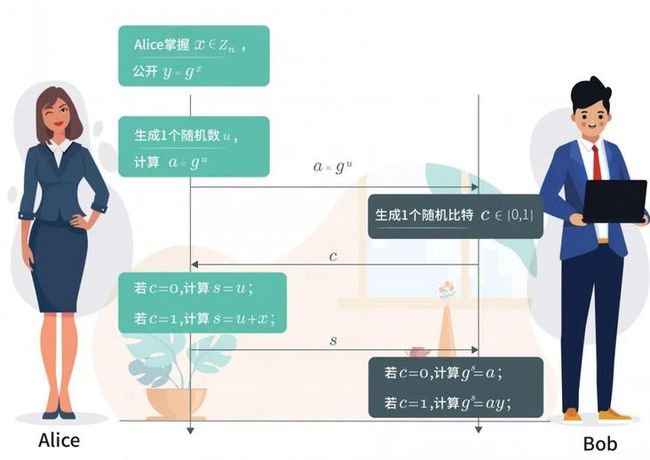
接下来介绍Schnorr零知识证明协议:
令 =<>是阶群,为大素数,证明者拥有秘密知识 ∈,并公开系统公钥\( =^ \) 。
1. 证明者产生一个随机数∈,计算\( =^ \)并发送给验证者。
2. 验证者Bob产生一个随机数∈{0,1}并发送给证明者Alice。
3. 如果=0,证明者计算=;如果=1,证明者计算=+。之后证明者将发送给验证者。
4. 若=0,证明者验证=;如果=1,证明者计算\( ^= \)。
公钥\( =^ \),由于离散对数分解困难,因此无法直接根据\( ^ \)计算出。因为证明者根据的值选择发送+或者,若证明者不知道的值,那么当验证者发送=1时,证明者无法发出正确的=+,验证者在验证\( ^=^{+}=^· ^=· \)时就会验证失败。
想象一个攻击者Tom,他知道Bob之后产生的为什么值。则Tom可以任()意构造,若=0则让\( =^ \);若=1则让= 。即只要攻击者知道Bob之后产生的具体为什么值,Tom都可构造一个,使得Bob认为Tom知道的值,虽然Tom其实并不知道,只知道Bob会产生的的值,即Bob并不知道的任何信息,所以无法区分出Alice和Tom。
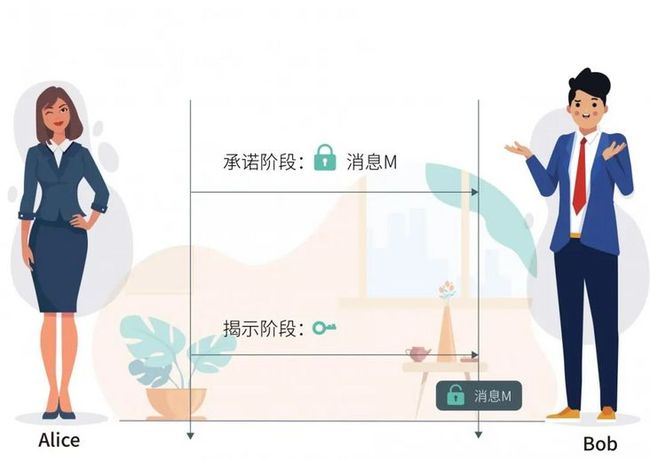
比特承诺
比特承诺(Bit Commitment),最早在1995年由图灵奖获得者Blum首先提出。
比特承诺分为两个阶段,第一个阶段为承诺阶段,承诺者向验证者承诺秘密值,并向验证者发送对验证者保密的秘密值。
第二个阶段是揭示阶段,承诺者向验证者揭示第一个阶段承诺的确实是,同时验证者得知秘密值的内容。也可以简单理解成承诺阶段,承诺方将一个消息锁进一个盒子里,再将该消息发送给验证方。
验证阶段,承诺方将盒子打开,向验证方展示盒子里的内容,以证明自己确实将消息锁在盒子里发送给了验证方。
接下来介绍一个基于强单向函数(哈希函数)的承诺方案,将该强单向函数记为ℎ()(满足找出任意两个和,使得()=()不可行;已知(),无法求出;任意两个不同的和,无法区分出()和()哪个的原像是):
承诺阶段:
1. Alice产生两个随机数\( _1,_2 \)。
2. Alice将随机数\( _1,_2 \)与自己将要承诺的消息M进行连接,记为\( _1,_2, \)。
3. Alice计算\( _1,_2, \)的哈希值\( =ℎ(_1,_2,) \),并将和\( _1 \)发送给Bob,作为Alice对消息m的承诺。
揭示阶段:
1. Alice将\( _1,_2, \)告知Bob
2. Bob 计算\( _1,_2, \)的哈希值′,并将′的值与进行比较,如果匹配,则承诺有效。
由于Hash的抗一次原像性(preimage resistance),Bob无法根据ℎ(1,2,)计算出,保证了计算意义上的隐藏性,Bob的计算力无法计算出。
若Hash满足对于任意,函数\( ℎ_(_1,_2) = ℎ(_1,_2,) \)都是规则的(即每个像的原像个数都相同),那么\( ℎ(_1,_2,) \)在信息论意义上隐藏了,因为的取值与\( ℎ(_1,_2,) \)是独立的,即对于任意!=′,任意取值都满足
\( [ℎ(_1,_2,)=]=[ℎ(_1,_2,′) = ] \)
通俗的说,Bob即使有无限的计算力,计算出满足\( ℎ()=ℎ(_1,_2,) \)的所有的集合,中任意一个元素是(\( _1,_2, \))的概率也都相同,Bob猜对的概率只有1/||。
在实际中,我们通常可假设Hash(*)是一个随机预言机(random oracle),且\( _1 \)和\( _2 \)足够长,保证ℎ是接近规则的,在统计意义上隐藏了的信息。