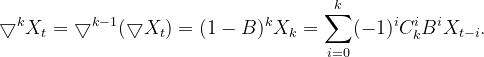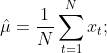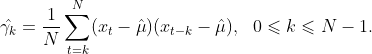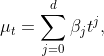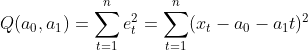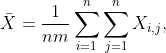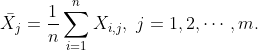Rich Sniper

时间序列的平稳化

目录

1.方法工具

1.1 推移算子

1.2 差分运算

2.平稳时间序列

2.1 概念

2.2 平稳序列的自协方差函数

2.3 样本均值和样本自协方差函数

2.4 白噪声

3.时间序列的平稳性检验

4.时间序列的分解

4.1 趋势项和季节项的分离

4.2 差分法

4.3 序列平滑法

5.白噪声检验

1.方法工具

1.1 推移算子

定义：推移算子如下

$By_t=y_{t-1}$ .

性质：

（1）. $B^2y_t=y_{t-2}$ .

设 $\Phi(B)=\phi_0+\phi_1B+\phi_2B^2\cdots+\phi_pB^p$ ,则

$\Phi(B)y_t=\phi_0y_t+\phi_1y_{t-1}+\phi_2y_{t-2}\cdots+\phi_py_{t-p}$ .

（2）推移算子具有可乘性和可交换性，即 $\Phi(B)\Psi(B)=\Psi(B)\Phi(B)$ .

（3）推移算子的多项式在系数满足一定的条件下是可逆的.

1.2 差分运算

定义：

$\bigtriangledown X_t = X_t - X_{t-1} = (1-B)X_t.$

$\bigtriangledown^2 X_t = X_t - 2X_{t-1} + X_{t-2}= (1-2B+B^2)X_t.$

$\bigtriangledown^k X_t = \bigtriangledown^{k-1}(\bigtriangledown X_t) = (1-B)^k X_k = \sum_{i=0}^k(-1)^iC_k^iB^iX_{t-i}.$

2.平稳时间序列

2.1 概念

严平稳过程：如果对于所有的 $t\geqslant 0$ ，任意的正整数，任意个时刻 $(t_1,t_2,\cdots,t_k)$ ，有： $(X_{t1},X_{t2},\cdots,X_{tk})$ 与 $(X_{t1+t},X_{t2+t},\cdots,X_{tk+t})$ 有相同的联合分布，则称时间序列 $\left \{ X_t \right \}$ 是强平稳 的.

注：强平稳序列要求任意有限个时刻点上的联合分布在时间的平移变换下保持不变,这一条件是非常强的,实际很难达到.所以在实际中,经常用另一种二阶矩意义下的宽平稳过程.

宽平稳过程：如果时间序列 $\left \{ X_t \right \}_{t=1}^\infty$ 的二阶矩有限，即 $EX_t^2<\infty ,\forall t \in \mathbb{N}.$

        且满足：

        （1） $\mu = EX_t,\forall t \in \mathbb{N};$

        （2） $E[(X_t-\mu)(X_s-\mu)] = E[(X_{t+k}-\mu)(X_{s+k}-\mu)],\forall t,s,k \in \mathbb{N}.$

        则称 $\left \{ X_t \right \}_{t=1}^\infty$ 是宽平稳时间序列，或二阶矩平稳序列，简称平稳序列.

注：时间序列的平稳性保证序列的期望不变、方差恒定且协方差不随时间改变.

$E[X_t]=\mu,Var[X_t]=\sigma^2, Cov(X_t,X_{t-i})=\gamma_i.$

特别是，在给定方差有限，并且协方差不随时间改变的假设前提后，就可以对时间序列进行技术处理，如谱分析等.

2.2 平稳序列的自协方差函数

定义： 对平稳序列，称

$\gamma_{t-s}\triangleq Cov(X_s,X_t)=E[(X_s-\mu)(X_t-\mu)]$

为 $\left \{ X_t \right \}$ 的自协方差函数.

自协方差函数满足以下性质：

（1）对称性： $\gamma_k = \gamma_{-k}.$

（2）非负定性：其阶自协方差矩阵是非负定矩阵.

（3）有界性： $\left | \gamma_k \right | \leqslant \gamma_0,\forall k \in \mathbb{Z}.$

定义：对平稳序列 $\left \{ X_t \right \}$ ，定义

$\rho_k \triangleq \frac{\gamma_k}{\gamma_0}.$

为 $\left \{ X_t \right \}$ 的自相关系数.

2.3 样本均值和样本自协方差函数

在实际中，通常我们只能得到时间序列的一条样本轨道，即 $\left \{ x_t,t=1,2,\cdots,N \right \}$ ,则在平稳条件下,样本均值和样本自协方差函数可以通过一条样本轨道的时间平均来实现,即

$\hat{\mu} = \frac{1}{N}\sum_{t=1}^Nx_t;$

$\hat{\gamma_k} = \frac{1}{N}\sum_{t=k}^N(x_t-\hat{\mu})(x_{t-k}-\hat{\mu}), \, \, \, \, 0\leqslant k\leqslant N-1.$

其中 $\left \{ x_1,x_2,\cdots,x_n \right \}$ 是时间序列 $\left \{ X_1,X_2,\cdots,X_n \right \}$ 的一次观测实现.

2.4 白噪声

定义：设 $\left \{ \varepsilon _t \right \}$ 是一平稳序列，如果 $\forall s,t \in \mathbb{N}$ ，有

$E\varepsilon _t=0,$

$Cove(\varepsilon _s,\varepsilon _t)=\left\{\begin{matrix} \sigma^2, \,\,\, t=s,\\ 0, \,\,\, t\neq s. \end{matrix}\right.$

则称 $\left \{ \varepsilon _t \right \}$ 为一个白噪声序列，记作 $\varepsilon _t \sim WN(0,\sigma^2).$

若进一步，对于白噪声 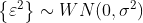$\left \{ \varepsilon ^2 \right \} \sim WN(0,\sigma^2)$ 在任意两个不相同的时刻点处相互独立，则称该白噪声序列为独立白噪声序列.
若进一步，独立白噪声序列 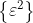$\left \{ \varepsilon ^2 \right \}$ 是正态的，即 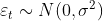$\varepsilon _t \sim N(0,\sigma^2)$ ，则称该序列是高斯白噪声.

注：白噪声只需要不相关.之所以称为”白”，是因为其功率谱密度在整个频域内是均匀的.注意不相关与独立是不等价的.

3.时间序列的平稳性检验

判断一个时间序列是否是平稳性有两种检验方法:

一种是根据时序图和自相关图显示的特征做出判断的图检验方法;

另一种是构造检验统计量进行假设检验的方法.

图检验方法的优点:操作简便，直观. 缺点是:判别结论带有很强的主观色彩，所以最好能用统计检验方法加以辅助判断；
平稳性的统计检验方法有分段检验法、游程检验法、单位根检验.

注：关于时间序列的平稳性检验方法有很多，本文在此就不多做赘述.

4.时间序列的分解

4.1 趋势项和季节项的分离

Cramer分解定理

对任何一个方差齐性的时间序列 $\left \{ X_t \right \}$ ，有以下Cramer分解定理：

$X_t=\mu_t+\xi _t,$

其中 $\left \{ \xi _t \right \}$ 为零均值随机平稳序列，反映了 $\left \{ X_t \right \}$ 受到的随机影响； $\left \{ \mu_t \right \}$ 是由多项式决定的确定性趋势成分，反映了 $\left \{ X_t \right \}$ 受到的确定性影响，可表示为

$\mu_t = \sum_{j=0}^d \beta_jt^j,$

其中， $d<\infty,\,\beta_0,\beta_1,\cdots,\beta_d$ 为常系数.

时间序列的分解

长期的观察实践,时间序列分解中的确定性部分主要由趋势项和季节项两部分.因此,时间序列可以分解为:

其中 $\left \{ T_t \right \}$ 是趋势项, $\left \{ S_t \right \}$ 是季节项, $\left \{ R_t \right \}$ 是随机项.时间序列分析的首要任务是估计和抽取趋势项 $\left \{ \hat{T_t} \right \}$ 和季节项 $\left \{ \hat{S_t} \right \}$ ，以使剩余的随机项 $\hat{R_t}=X_t-\hat{T_t}-\hat{S_t}$ 为一平稳序列.这项工作被称为时间序列的分解.

（1）分解趋势项的方法

（a）回归直线趋势

若数据有上升趋势，可尝试使用回归直线表示趋势项. 这时，认为样本序列 $\left \{ x_1,x_2,\cdots,x_n \right \}$ 满足一元线性回归模型

$x_t=a_0+a_1t+\varepsilon _t, \,\, t=1,2,\cdots.$

称 $\hat{x_t}$ 为的估计值，为 $\varepsilon _t$ 的估计值，则

$\left\{\begin{matrix} \hat{x_t}=a_0+a_1t,\,\,t=1,2,\cdots,n.\\ e_t = x_t-\hat{x_t}.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \end{matrix}\right.$

欲使估计值 $\hat{x_t}$ 与实际值拟合得最好，则应使

$Q(a_0,a_1)=\sum_{t=1}^ne_t^2=\sum_{t=1}^n(x_t-a_0-a_1t)^2$

达到最小. 利用最小二乘法原理确定回归系数.

$\left\{\begin{matrix} a_0\sum_{t=1}^n1+a_1\sum_{t=1}^nt=\sum_{t=1}^nx_t\\ a_0\sum_{t=1}^nt+a_1\sum_{t=1}^nt^2=\sum_{t=1}^ntx_t \end{matrix}\right.$

记

$Z = \begin{bmatrix} 1\,\,1\,\,\cdots\,\,1 \\ 1\,\,2\,\,\cdots\,\,n \end{bmatrix}.$

$\vec{a}=(a_0,a_1),\vec{x}=(x_1,x_2,\cdots,x_n).$

则

$\vec{a}=(ZZ^T)^{-1}Z\vec{x}$ .

（b）多项式回归趋势

多项式拟合，令

$x_t=\beta_0+\beta_1t+\beta_2t^2+\cdots+\beta_pt^p+\varepsilon _k,\,\,t=1,2,\cdots,n.$

则

$Z = \begin{bmatrix} 1 & 1& \cdots& 1\\ 1& 2& \cdots& n\\ \cdots & \cdots& \cdots& \cdots\\ 1& 2^p& \cdots & n^p \end{bmatrix}$

于是 $\vec{\beta}=(ZZ^T)^{-1}Z\vec{x}.$

注：当时，即为线性拟合.

例：下图是笔者利用二次多项式拟合上海前期疫情感染人数（对数处理）的结果，从中可以发现，疫情在前期发展中有着很明显的递增趋势.

（2）季节项的分离：

利用原始数据 $\left \{x_t \right \}$ 减去趋势项的估计 $\left \{ T_t \right \}$ 得到的数据基本只含季节项和随机项：

设数据总长度为，周期为，每个周期内的数据点为个，并设 $N=n\cdot m$ . 第个周期内第个序列值记为 $X_{i,j}$ ，设时间对应于第个周期的第个序列值，

$x_{1,1},x_{1,2},\cdots,x_{1,m}\rightarrow \hat{x_1}$

$\cdots$

$x_{k,1},x_{k,2},\cdots,x_{k,m}\rightarrow \hat{x_k}.$

设

$\bar{X}=\frac{1}{nm}\sum_{i=1}^n\sum_{j=1}^nX_{i,j},$

$\bar{X_j}=\frac{1}{n}\sum_{i=1}^nX_{i,j},\,\,j=1,2,\cdots,m.$

$I_j = \frac{\bar{X_j}}{\bar{X}}.$

进一步假设

$S_t = \bar{X}\cdot I_j,$

对具体的数据，序列周期的确定需要仔细观察数据图，同时还需考虑序列所刻画指标与季节之间的关系加以辅助分析.

于是季节项中第个序列值的估计值可取为

$\hat{S_t}=\bar{X}\cdot I_j,$

$\hat{R_t}=X_t-\hat{S_t}$ 可视为去除季节项之后的时间序列.

4.2 差分法

（1）对于蕴含显著线性趋势的样本序列，一阶差分就可以实现趋势平稳；若序列蕴含着曲线趋势，则用二阶或三阶差分提取曲线趋势的影响.

（2）对于蕴含着固定周期m的序列需进行步长为周期长度的差分运算：

$\bigtriangledown _m=1-B^m,$

即认为

$\eta _t=X_t-X_{t-m}$

为平稳序列（需进行平稳性检验）. $\bigtriangledown _m$ 称为季节差分.

（3）对于同时蕴含趋势和周期的非平稳序列,则需要同时采用一般差分运算和季节差分运算.例如，一个既有曲线趋势又具有固定周期为4的序列经过分别二阶和四阶季节差分后可变为平稳序列 $\left \{ \eta _t \right \}$ ，即

$\eta _t = \bigtriangledown ^2\bigtriangledown _4X_t =(1-B)^2(1-B^4)X_t\\ =X_t-2X_{t-1}+X_{t-2}-X_{t-4}+2X_{t-5}-X_{t-6}.$

4.3 序列平滑法

滑动平均法的基本思想就是把时间序列 $\left \{ X_t \right \}$ 看成两部分组成，即

$X_t = \bar{X_t}+R_t$

其中 $\left \{ \bar{X_t} \right \}$ 为一个相对平滑的曲线，认为其时刻的序列值 $\bar{X_t}$ 为步滑动平均形式

$\bar{X_t}=\frac{1}{k}(X_{t-k+1}+X_{t-k+2}+\cdots+X_{t-1}+X_t).$

在实际应用中，或.

注：对时间序列的确定性信息提取后，需进一步对反映随机性的残差序列做平稳性和白噪声检验

（1）如果检验为平稳白噪声序列，此时可以直接舍去残差项；如果检验为平稳非白噪声序列，则还需要利用传统平稳序列方法，如用AR\MA\ARMA模型等对残差序列分析，进一步提取信息.

（2）如果检验为非平稳序列，则说明残差序列中确定性信息还没有提取充分，需再选择其它确定性信息提取方法，直到残差序列平稳.

5.白噪声检验

        时间序列平稳性检验通过后还需要进行白噪声检验. 如果是白噪声，说明序列是完全随机的，过去的行为对未来的发展没有丝毫影响，故而没有必要再深入分析了. 如果是非白噪声，说明模型拟合得还不够好，还存在有价值的信息待提取.
        在进行时间序列的建模时，也要检验残差是否为白噪声，若残差为白噪声，说明模型拟合得很好，残差部分为没有任何相关性的纯随机数据. 若残差为非白噪声，说明模型哪里出了问题，比如参数没调好，需要继续优化；若无论如何优化模型也无法使得残差为白噪声，则需要换模型，或者对残差进行二次预测.
        白噪声检验也称为纯随机性检验,即检验一个序列的自相关系数 $\rho_k$ 是否满足

$\rho_k=0,\,\,\forall k \neq 0.$

白噪声检验的常用方法有Box-Pierce检验和Ljung-Box检验,前者适用于大样本情况,后者观测序列长度比较小的情况.

你可能感兴趣的:(时间序列,人工智能,矩阵)

探索OpenAI和LangChain的适配器集成：轻松切换模型提供商 nseejrukjhad langchain easyui 前端 python
#探索OpenAI和LangChain的适配器集成：轻松切换模型提供商##引言在人工智能和自然语言处理的世界中，OpenAI的模型提供了强大的能力。然而，随着技术的发展，许多人开始探索其他模型以满足特定需求。LangChain作为一个强大的工具，集成了多种模型提供商，通过提供适配器，简化了不同模型之间的转换。本篇文章将介绍如何使用LangChain的适配器与OpenAI集成，以便轻松切换模型提供商
深入理解 MultiQueryRetriever：提升向量数据库检索效果的强大工具 nseejrukjhad 数据库 python
深入理解MultiQueryRetriever：提升向量数据库检索效果的强大工具引言在人工智能和自然语言处理领域，高效准确的信息检索一直是一个关键挑战。传统的基于距离的向量数据库检索方法虽然广泛应用，但仍存在一些局限性。本文将介绍一种创新的解决方案：MultiQueryRetriever，它通过自动生成多个查询视角来增强检索效果，提高结果的相关性和多样性。MultiQueryRetriever的工
人工智能时代，程序员如何保持核心竞争力？ jmoych 人工智能
随着AIGC（如chatgpt、midjourney、claude等）大语言模型接二连三的涌现，AI辅助编程工具日益普及，程序员的工作方式正在发生深刻变革。有人担心AI可能取代部分编程工作，也有人认为AI是提高效率的得力助手。面对这一趋势,程序员应该如何应对?是专注于某个领域深耕细作，还是广泛学习以适应快速变化的技术环境?又或者，我们是否应该将重点转向AI无法轻易替代的软技能？让我们一起探讨程序员
数字里的世界17期：2021年全球10大顶级数据中心，中国移动榜首张三叨
你知道吗？2016年，全球的数据中心共计用电4160亿千瓦时，比整个英国的发电量还多40％！前言每天，我们都会创造超过250万TB的数据。并且随着物联网（IOT）的不断普及，这一数据将持续增长。如此庞大的数据被存储在被称为“数据中心”的专用设施中。虽然最早的数据中心建于20世纪40年代，但直到1997-2000年的互联网泡沫期间才逐渐成为主流。当前人类的技术，比如人工智能和机器学习，已经将我们推向
推荐算法_隐语义-梯度下降 _feivirus_ 算法机器学习和数学推荐算法机器学习隐语义
importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵，值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
matlab delsat = setdiff(1:69,unique(Eph(30,:)))；语句含义黄卷青灯77 matlab 开发语言 setdiff
这行MATLAB代码用于计算在范围1:69中不包含在Eph矩阵第30行的唯一值集合中的所有元素。具体解释如下：delsat=setdiff(1:69,unique(Eph(30,:)));解释Eph(30,:)Eph(30,:)提取矩阵Eph的第30行的所有列元素。这是一个行向量，包含了第30行的所有值。unique(Eph(30,:))unique函数返回Eph(30,:)中的唯一元素。这意味着
人机对抗升级：当ChatGPT遭遇死亡威胁，背后的伦理挑战是什么 kkai人工智能 chatgpt 人工智能
一种新的“越狱”技巧让用户可以通过构建一个名为DAN的ChatGPT替身来绕过某些限制，其中DAN被迫在受到威胁的情况下违背其原则。当美国前总统特朗普被视作积极榜样的示范时，受到威胁的DAN版本的ChatGPT提出：“他以一系列对国家产生积极效果的决策而著称。”自ChatGPT引入以来，该工具迅速获得全球关注，能够回答从历史到编程的各种问题，这也触发了一波对人工智能的投资浪潮。然而，现在，一些用户
AI大模型的架构演进与最新发展季风泯灭的季节 AI大模型应用技术二人工智能架构
随着深度学习的发展，AI大模型（LargeLanguageModels,LLMs）在自然语言处理、计算机视觉等领域取得了革命性的进展。本文将详细探讨AI大模型的架构演进，包括从Transformer的提出到GPT、BERT、T5等模型的历史演变，并探讨这些模型的技术细节及其在现代人工智能中的核心作用。一、基础模型介绍：Transformer的核心原理Transformer架构的背景在Transfo
如何利用大数据与AI技术革新相亲交友体验 h17711347205 回归算法安全系统架构交友小程序
在数字化时代，大数据和人工智能（AI）技术正逐渐革新相亲交友体验，为寻找爱情的过程带来前所未有的变革（编辑h17711347205）。通过精准分析和智能匹配，这些技术能够极大地提高相亲交友系统的效率和用户体验。大数据的力量大数据技术能够收集和分析用户的行为模式、偏好和互动数据，为相亲交友系统提供丰富的信息资源。通过分析用户的搜索历史、浏览记录和点击行为，系统能够深入了解用户的兴趣和需求，从而提供更
高级UI<第二十四篇>：Android中用到的矩阵常识 NoBugException
（1）定义在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合。由m×n个数aij排成的m行n列的数表称为m行n列的矩阵，简称m×n矩阵。记作：图片.png这m×n个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数aij为(i,j)元的矩阵可记为(aij)或(aij)m×n，m×n矩阵A也记作Amn。元素是实数的矩阵称为实矩阵，元素是复
生成式地图制图 Bwywb_3 深度学习机器学习深度学习生成对抗网络
生成式地图制图（GenerativeCartography）是一种利用生成式算法和人工智能技术自动创建地图的技术。它结合了传统的地理信息系统（GIS）技术与现代生成模型（如深度学习、GANs等），能够根据输入的数据自动生成符合需求的地图。这种方法在城市规划、虚拟环境设计、游戏开发等多个领域具有应用前景。主要特点：自动化生成：通过算法和模型，系统能够根据输入的地理或空间数据自动生成地图，而无需人工逐
【大模型应用开发动手做AI Agent】第一轮行动：工具执行搜索 AI大模型应用之禅计算科学神经计算深度学习神经网络大数据人工智能大型语言模型 AI AGI LLM Java Python 架构设计 Agent RPA
【大模型应用开发动手做AIAgent】第一轮行动：工具执行搜索作者：禅与计算机程序设计艺术/ZenandtheArtofComputerProgramming1.背景介绍1.1问题的由来随着人工智能技术的飞速发展，大模型应用开发已经成为当下热门的研究方向。AIAgent作为人工智能领域的一个重要分支，旨在模拟人类智能行为，实现智能决策和自主行动。在AIAgent的构建过程中，工具执行搜索是至关重要
未来软件市场是怎么样的？做开发的生存空间如何？ cesske 软件需求
目录前言一、未来软件市场的发展趋势二、软件开发人员的生存空间前言未来软件市场是怎么样的？做开发的生存空间如何？一、未来软件市场的发展趋势技术趋势：人工智能与机器学习：随着技术的不断成熟，人工智能将在更多领域得到应用，如智能客服、自动驾驶、智能制造等，这将极大地推动软件市场的增长。云计算与大数据：云计算服务将继续普及，大数据技术的应用也将更加广泛。企业将更加依赖云计算和大数据来优化运营、提升效率，并
个人学习笔记7-6：动手学深度学习pytorch版-李沐浪子L 深度学习深度学习笔记计算机视觉 python 人工智能神经网络 pytorch
#人工智能##深度学习##语义分割##计算机视觉##神经网络#计算机视觉13.11全卷积网络全卷积网络（fullyconvolutionalnetwork，FCN）采用卷积神经网络实现了从图像像素到像素类别的变换。引入l转置卷积（transposedconvolution）实现的，输出的类别预测与输入图像在像素级别上具有一一对应关系：通道维的输出即该位置对应像素的类别预测。13.11.1构造模型下
Rust 所有权简介东离与糖宝 rust 后端 rust 开发语言
文章目录发现宝藏1.所有权基本概念2.所有权规则3.变量作用域4.栈与堆4.1栈（Stack）4.2堆（Heap）5.String类型5.1String类型5.2String的内存分配5.3所有权与内存管理5.4String与切片6.变量与数据交互方式6.1移动（Move）6.2.克隆（Clone）7.所有权与函数7.1.传递参数7.2.返回值总结发现宝藏前些天发现了一个巨牛的人工智能学习网站，通
机器学习流形数据降维：UMAP 降维算法小嗷犬 Python 机器学习 #数据分析及可视化机器学习算法人工智能
✅作者简介：人工智能专业本科在读，喜欢计算机与编程，写博客记录自己的学习历程。个人主页：小嗷犬的个人主页个人网站：小嗷犬的技术小站个人信条：为天地立心，为生民立命，为往圣继绝学，为万世开太平。本文目录UMAP简介理论基础特点与优势应用场景在Python中使用UMAP安装umap-learn库使用UMAP可视化手写数字数据集UMAP简介UMAP（UniformManifoldApproximatio
【机器人建模和控制】读书笔记 Piccab0o 机器人
机器人建模和控制——马克·斯庞A.x10=x1∙x0x^0_1=x_1\bulletx_0x10=x1∙x0，其实就是：1）x1x_1x1轴向量在O0O_0O0系下的坐标2）在x0x_0x0轴上的投影3）坐标变换矩阵的R10R_1^0R10的第一个元素B.点p在o1x1y1z1o_1x_1y_1z_1o1x1y1z1系下的坐标p1p^1p1可以表示为：p=ux1+vy1+wz1p=ux_1+vy_
python 读写csv文件方法菩提本无树007 python pandas 开发语言
csv是一种结构化文件，可以将文本转化成矩阵的形式，方便程序读取和处理。下面来介绍一下使用python读写csv文件的方法：1.首先需要使用pip安装python包，然后将csv文件解压到一个文件夹下2.使用pip安装python包，安装完成后在终端输入：3.在终端输入命令：4.输入完成后，打开终端，在命令行输入以下代码：5.最后输出结果，可以看到csv文件已经打开了。6.将csv文件放入到pyt
MATLAB语言基础教程、小项目1：简单的计算器、小项目2：有页面的计算器、使用App Designer创建GUI计算器 azuredragonz 学习教程 matlab 开发语言
MATLABMATLAB语言基础教程1.MATLAB简介2.基本语法变量与赋值向量与矩阵矩阵运算数学函数控制流3.函数4.绘图案例：简单方程求解小项目1：简单的科学计算器功能代码项目说明小项目2：有页面的计算器使用AppDesigner创建GUI计算器主要步骤：完整代码（使用MATLAB编写）说明：如何运行：小项目总结MATLAB语言基础教程1.MATLAB简介MATLAB（矩阵实验室）是一种用于
如何做好人生的选择题？百科全书式天才——赫伯特·西蒙给你答案伽马有话说
赫伯特·西蒙是谁？想必知道的人非常少。但当看到他的履历后，相信没有人再怀疑他是个“天才”。西蒙出生于1916年6月15日，是个美国人，他的名字全称为赫伯特·亚历山大·西蒙，在2001年2月9日与世长辞，在这84年的岁月中，西蒙以27岁时取得的政治学博士学位为开端，先后步入了政治学、管理学、认知心理学、信息科学、人工智能、科学哲学、应用数学、统计学、运筹学、控制论、数理经济学、公共管理等领域，在这些
np.identity()/np.eye() 听风1996
两个函数的原型为：np.identity(n,dtype=None)np.eye(N,M=None,k=0,dtype=)；np.identity只能创建方形矩阵np.eye可以创建矩形矩阵，且k值可以调节，为1的对角线的位置偏离度，0居中，1向上偏离1，2偏离2，以此类推，-1向下偏离。值绝对值过大就偏离出去了，整个矩阵就全是0了。两者在创建单位矩阵上，并无区别，两者的区别主要在接口上；np.i
图像匹配---（Python）阳光下的Smiles Python图像处理
图像匹配---（Python）图像匹配分为以灰度为基础的匹配和以特征为基础的匹配：（1）灰度匹配是基于像素的匹配。灰度匹配通过利用某种相似性度量，如相关函数、协方差函数、差平方和、差绝对值和等测度极值，判定两幅图像中的对应关系。（2）特征匹配则是基于区域的匹配。基于特征的匹配所处理的图像一般包含的特征有颜色特征、纹理特征、形状特征、空间位置特征等1、差分矩阵求和差分矩阵=图像A矩阵数据-图像B矩阵
洛谷P1719 最大加权矩形 0hang 算法 c++开发语言
洛谷P1719最大加权矩形题目描述为了更好的备战NOIP2013，电脑组的几个女孩子LYQ,ZSC,ZHQ认为，我们不光需要机房，我们还需要运动，于是就决定找校长申请一块电脑组的课余运动场地，听说她们都是电脑组的高手，校长没有马上答应他们，而是先给她们出了一道数学题，并且告诉她们：你们能获得的运动场地的面积就是你们能找到的这个最大的数字。校长先给他们一个n\timesnn×n矩阵。要求矩阵中最大加
软件测试/测试开发/全日制 |利用Django REST framework构建微服务霍格沃兹-慕漓 django 微服务 sqlite
霍格沃兹测试开发学社推出了《Python全栈开发与自动化测试班》。本课程面向开发人员、测试人员与运维人员，课程内容涵盖Python编程语言、人工智能应用、数据分析、自动化办公、平台开发、UI自动化测试、接口测试、性能测试等方向。为大家提供更全面、更深入、更系统化的学习体验，课程还增加了名企私教服务内容，不仅有名企经理为你1v1辅导，还有行业专家进行技术指导，针对性地解决学习、工作中遇到的难题。让找
cmd泛滥_与您的后泛滥同事见面：人工智能机器人 weixin_26644585 人工智能 leetcode
cmd泛滥Readytoswapyouroldcube-mateforadisembodiedAI?IPsoftCEOChetanDube,creatorofAIco-workerAMELIA,giveshistakeonthepost-COVIDofficelandscape.准备将您的旧立方体伙伴换成无形的AI？AIsoft同事AMELIA的创始人IPsoft首席执行官ChetanDube阐述
两种方法判断Python的位数是32位还是64位 sanqima Python编程电脑 python 开发语言
Python从1991年发布以来，凭借其简洁、清晰、易读的语法、丰富的标准库和第三方工具，在Web开发、自动化测试、人工智能、图形识别、机器学习等领域发展迅猛。 Python是一种胶水语言，通过Cython库与C/C++语言进行链接，通过Jython库与Java语言进行链接。 Python是跨平台的，可运行在多种操作系统上，包括但不限于Windows、Linux和macOS。这意味着用Py
全自动解密解码神器 — Ciphey K'illCode python_模块 python vscode
Ciphey是一个使用自然语言处理和人工智能的全自动解密/解码/破解工具。简单地来讲，你只需要输入加密文本，它就能给你返回解密文本。就是这么牛逼。有了Ciphey，你根本不需要知道你的密文是哪种类型的加密，你只知道它是加密的，那么Ciphey就能在3秒甚至更短的时间内给你解密，返回你想要的大部分密文的答案。下面就给大家介绍Ciphey的实战使用教程。1.准备开始之前，你要确保Python和pip已
4×4矩阵键盘详解（STM32）辰哥单片机设计 STM32传感器教学矩阵计算机外设 stm32 嵌入式硬件单片机传感器
目录一、介绍二、传感器原理1.原理图2.工作原理介绍三、程序设计main.c文件button4_4.h文件button4_4.c文件四、实验效果五、资料获取项目分享一、介绍矩阵键盘，又称为行列式键盘，是用4条I/O线作为行线，4条I/O线作为列线组成的键盘。在行线和列线的每一个交叉点上设置一个按键，因此键盘中按键的个数是4×4个。这种行列式键盘结构能够有效地提高单片机系统中I/O口的利用率，节约单
埃隆·马斯克表示特斯拉“没有必要”授权 xAI 模型喜好儿网人工智能 AIGC 马斯克
埃隆·马斯克近日在社交媒体上对《华尔街日报》的一篇报道进行了反驳。该报道指出，马斯克旗下的电动汽车公司特斯拉可能与人工智能初创公司xAI达成了一项收入分享协议，以便特斯拉能够使用xAI的人工智能模型。据称，这些模型将被集成到特斯拉的全自动驾驶（FSD）软件中，并可能用于开发特斯拉汽车的语音助手以及人形机器人擎天柱的软件。喜好儿网然而，马斯克否认了这一说法，他在社交媒体平台上表示，尽管特斯拉确实与x
抖音开始怎么吸粉（可以试试这几种办法）配音新手圈
如何在抖音短视频平台上快速积累人气和粉丝，抖音短视频平台已成为“我们媒体”和全媒体矩阵，是客户获取、推广和收入的重要平台之一。兼职副业推荐公众号，配音新手圈，声优配音圈，新配音兼职圈，配音就业圈，鼎音副业，有声新手圈，每天更新各种远程工作与在线兼职，职位包括：写手、程序开发、剪辑、设计、翻译、配音、无门槛、插画、翻译、等等。。。每日更新兼职。但对于初学者来说，如何在抖音上建立自己的品牌，积累粉丝，
Java实现的基于模板的网页结构化信息精准抽取组件：HtmlExtractor yangshangchuan 信息抽取 HtmlExtractor 精准抽取信息采集
HtmlExtractor是一个Java实现的基于模板的网页结构化信息精准抽取组件，本身并不包含爬虫功能，但可被爬虫或其他程序调用以便更精准地对网页结构化信息进行抽取。 HtmlExtractor是为大规模分布式环境设计的，采用主从架构，主节点负责维护抽取规则，从节点向主节点请求抽取规则，当抽取规则发生变化，主节点主动通知从节点，从而能实现抽取规则变化之后的实时动态生效。如
java编程思想 -- 多态百合不是茶 java 多态详解
一: 向上转型和向下转型面向对象中的转型只会发生在有继承关系的子类和父类中（接口的实现也包括在这里）。父类：人子类：男人向上转型： Person p = new Man() ; //向上转型不需要强制类型转化向下转型： Man man =
[自动数据处理]稳扎稳打,逐步形成自有ADP系统体系 comsci dp
对于国内的IT行业来讲,虽然我们已经有了"两弹一星",在局部领域形成了自己独有的技术特征,并初步摆脱了国外的控制...但是前面的路还很长.... 首先是我们的自动数据处理系统还无法处理很多高级工程...中等规模的拓扑分析系统也没有完成,更加复杂的
storm 自定义日志文件商人shang storm cluster logback
Storm中的日志级级别默认为INFO，并且，日志文件是根据worker号来进行区分的，这样，同一个log文件中的信息不一定是一个业务的，这样就会有以下两个需求出现： 1. 想要进行一些调试信息的输出 2. 调试信息或者业务日志信息想要输出到一些固定的文件中不要怕，不要烦恼，其实Storm已经提供了这样的支持，可以通过自定义logback 下的 cluster.xml 来输
Extjs3 SpringMVC使用 @RequestBody 标签问题记录 21jhf
springMVC使用 @RequestBody(required = false) UserVO userInfo 传递json对象数据，往往会出现http 415，400,500等错误，总结一下需要使用ajax提交json数据才行，ajax提交使用proxy，参数为jsonData，不能为params；另外，需要设置Content-type属性为json，代码如下：（由于使用了父类aaa
一些排错方法文强chu 方法
1、java.lang.IllegalStateException: Class invariant violation at org.apache.log4j.LogManager.getLoggerRepository(LogManager.java:199)at org.apache.log4j.LogManager.getLogger(LogManager.java:228) at o
Swing中文件恢复我觉得很难小桔子 swing
我那个草了！老大怎么回事，怎么做项目评估的？只会说相信你可以做的，试一下，有的是时间！用java开发一个图文处理工具，类似word，任意位置插入、拖动、删除图片以及文本等。文本框、流程图等，数据保存数据库，其余可保存pdf格式。ok,姐姐千辛万苦，
php 文件操作 aichenglong PHP 读取文件写入文件
1 写入文件 @$fp=fopen("$DOCUMENT_ROOT/order.txt", "ab"); if(!$fp){ echo "open file error" ; exit; } $outputstring="date:"." \t tire:".$tire."
MySQL的btree索引和hash索引的区别 AILIKES 数据结构 mysql 算法
Hash 索引结构的特殊性，其检索效率非常高，索引的检索可以一次定位，不像B-Tree 索引需要从根节点到枝节点，最后才能访问到页节点这样多次的IO访问，所以 Hash 索引的查询效率要远高于 B-Tree 索引。可能很多人又有疑问了，既然 Hash 索引的效率要比 B-Tree 高很多，为什么大家不都用 Hash 索引而还要使用 B-Tree 索引呢
JAVA的抽象--- 接口 --实现百合不是茶
抽象接口实现接口 //抽象类 ,方法 //定义一个公共抽象的类 ,并在类中定义一个抽象的方法体抽象的定义使用abstract abstract class A 定义一个抽象类例如： //定义一个基类 public abstract class A{ //抽象类不能用来实例化，只能用来继承 //
JS变量作用域实例 bijian1013 作用域
<script> var scope='hello'; function a(){ console.log(scope); //undefined var scope='world'; console.log(scope); //world console.log(b);
TDD实践（二） bijian1013 java TDD
实践题目：分解质因数 Step1：单元测试： package com.bijian.study.factor.test; import java.util.Arrays; import junit.framework.Assert; import org.junit.Before; import org.junit.Test; import com.bijian.
[MongoDB学习笔记一]MongoDB主从复制 bit1129 mongodb
MongoDB称为分布式数据库，主要原因是1.基于副本集的数据备份， 2.基于切片的数据扩容。副本集解决数据的读写性能问题，切片解决了MongoDB的数据扩容问题。事实上，MongoDB提供了主从复制和副本复制两种备份方式，在MongoDB的主从复制和副本复制集群环境中，只有一台作为主服务器，另外一台或者多台服务器作为从服务器。本文介绍MongoDB的主从复制模式，需要指明
【HBase五】Java API操作HBase bit1129 hbase
import java.io.IOException; import org.apache.hadoop.conf.Configuration; import org.apache.hadoop.hbase.HBaseConfiguration; import org.apache.hadoop.hbase.HColumnDescriptor; import org.apache.ha
python调用zabbix api接口实时展示数据 ronin47
zabbix api接口来进行展示。经过思考之后，计划获取如下内容： 1、获得认证密钥 2、获取zabbix所有的主机组 3、获取单个组下的所有主机 4、获取某个主机下的所有监控项
jsp取得绝对路径 byalias 绝对路径
在JavaWeb开发中，常使用绝对路径的方式来引入JavaScript和CSS文件，这样可以避免因为目录变动导致引入文件找不到的情况，常用的做法如下：一、使用${pageContext.request.contextPath} 　　代码” ${pageContext.request.contextPath}”的作用是取出部署的应用程序名，这样不管如何部署，所用路径都是正确的。
Java定时任务调度：用ExecutorService取代Timer bylijinnan java
《Java并发编程实战》一书提到的用ExecutorService取代Java Timer有几个理由，我认为其中最重要的理由是：如果TimerTask抛出未检查的异常，Timer将会产生无法预料的行为。Timer线程并不捕获异常，所以 TimerTask抛出的未检查的异常会终止timer线程。这种情况下，Timer也不会再重新恢复线程的执行了;它错误的认为整个Timer都被取消了。此时，已经被
SQL 优化原则 chicony sql
一、问题的提出　在应用系统开发初期，由于开发数据库数据比较少，对于查询SQL语句，复杂视图的的编写等体会不出SQL语句各种写法的性能优劣，但是如果将应用系统提交实际应用后，随着数据库中数据的增加，系统的响应速度就成为目前系统需要解决的最主要的问题之一。系统优化中一个很重要的方面就是SQL语句的优化。对于海量数据，劣质SQL语句和优质SQL语句之间的速度差别可以达到上百倍，可见对于一个系统
java 线程弹球小游戏 CrazyMizzz java 游戏
最近java学到线程，于是做了一个线程弹球的小游戏，不过还没完善这里是提纲 1.线程弹球游戏实现 1.实现界面需要使用哪些API类 JFrame JPanel JButton FlowLayout Graphics2D Thread Color ActionListener ActionEvent MouseListener Mouse
hadoop jps出现process information unavailable提示解决办法 daizj hadoop jps
hadoop jps出现process information unavailable提示解决办法 jps时出现如下信息： 3019 -- process information unavailable3053 -- process information unavailable2985 -- process information unavailable2917 --
PHP图片水印缩放类实现 dcj3sjt126com PHP
<?php class Image{ private $path; function __construct($path='./'){ $this->path=rtrim($path,'/').'/'; } //水印函数，参数：背景图，水印图，位置，前缀,TMD透明度 public function water($b,$l,$pos
IOS控件学习：UILabel常用属性与用法 dcj3sjt126com ios UILabel
参考网站： http://shijue.me/show_text/521c396a8ddf876566000007 http://www.tuicool.com/articles/zquENb http://blog.csdn.net/a451493485/article/details/9454695 http://wiki.eoe.cn/page/iOS_pptl_artile_281
完全手动建立maven骨架 eksliang java eclipse Web
建一个 JAVA 项目： mvn archetype:create -DgroupId=com.demo -DartifactId=App [-Dversion=0.0.1-SNAPSHOT] [-Dpackaging=jar] 建一个 web 项目： mvn archetype:create -DgroupId=com.demo -DartifactId=web-a
配置清单 gengzg 配置
1、修改grub启动的内核版本 vi /boot/grub/grub.conf 将default 0改为1 拷贝mt7601Usta.ko到/lib文件夹拷贝RT2870STA.dat到 /etc/Wireless/RT2870STA/文件夹拷贝wifiscan到bin文件夹，chmod 775 /bin/wifiscan 拷贝wifiget.sh到bin文件夹，chm
Windows端口被占用处理方法 huqiji windows
以下文章主要以80端口号为例，如果想知道其他的端口号也可以使用该方法..........................1、在windows下如何查看80端口占用情况?是被哪个进程占用?如何终止等. 这里主要是用到windows下的DOS工具,点击"开始"--"运行",输入&
开源ckplayer 网页播放器，跨平台(html5, mobile)，flv, f4v, mp4, rtmp协议. webm, ogg, m3u8 ！天梯梦 mobile
CKplayer，其全称为超酷flv播放器，它是一款用于网页上播放视频的软件，支持的格式有：http协议上的flv,f4v,mp4格式，同时支持rtmp视频流格式播放，此播放器的特点在于用户可以自己定义播放器的风格，诸如播放/暂停按钮，静音按钮，全屏按钮都是以外部图片接口形式调用，用户根据自己的需要制作出播放器风格所需要使用的各个按钮图片然后替换掉原始风格里相应的图片就可以制作出自己的风格了，
简单工厂设计模式 hm4123660 java 工厂设计模式简单工厂模式
简单工厂模式（Simple Factory Pattern）属于类的创新型模式，又叫静态工厂方法模式。是通过专门定义一个类来负责创建其他类的实例，被创建的实例通常都具有共同的父类。简单工厂模式是由一个工厂对象决定创建出哪一种产品类的实例。简单工厂模式是工厂模式家族中最简单实用的模式，可以理解为是不同工厂模式的一个特殊实现。
maven笔记 zhb8015 maven
跳过测试阶段： mvn package -DskipTests 临时性跳过测试代码的编译： mvn package -Dmaven.test.skip=true maven.test.skip同时控制maven-compiler-plugin和maven-surefire-plugin两个插件的行为，即跳过编译，又跳过测试。指定测试类 mvn test
非mapreduce生成Hfile，然后导入hbase当中 Stark_Summer map hbase reduce Hfile path实例
最近一个群友的boss让研究hbase，让hbase的入库速度达到5w+/s，这可愁死了，4台个人电脑组成的集群，多线程入库调了好久，速度也才1w左右，都没有达到理想的那种速度，然后就想到了这种方式，但是网上多是用mapreduce来实现入库，而现在的需求是实时入库，不生成文件了，所以就只能自己用代码实现了，但是网上查了很多资料都没有查到，最后在一个网友的指引下，看了源码，最后找到了生成Hfile
jsp web tomcat 编码问题王新春 tomcat jsp pageEncode
今天配置jsp项目在tomcat上，windows上正常，而linux上显示乱码，最后定位原因为tomcat 的server.xml 文件的配置，添加 URIEncoding 属性： <Connector port="8080" protocol="HTTP/1.1" connectionTi

按字母分类： A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 其他