强化学习笔记(5)-回合策略梯度算法

以下为阅读《强化学习：原理与python实现》这本书第七章的学习笔记。

在之前学习到的强度学习方法中，都是通过学习最优价值函数来获得最优策略。现在换一个角度来思考，我们可以通过用含参函数来近似最优策略，并在迭代中更新参数值，这就是策略梯度算法。

用函数近似方法估计最优策略的基本思想是用含参函数来近似最优策略。由于任意策略都需要满足对于任意的状态，均有，我们也希望满足对于任意的，均有。为此我们可以引入动作偏好函数，使得

动作偏好函数可以具有线性组合或神经网络等多种形式，通过基于梯度的迭代算法来更新参数，就可以得到最优状态估计。

策略梯度定理

策略梯度定理给出了期望回报和策略梯度之间的关系，是策略梯度方法的基础

在回合制任务中，策略期望回报可以表示为，策略梯度定理给出了它对策略参数的梯度为

 策略梯度定理告诉我们，只要知道了的值，就可以得到期望回报的梯度。因此我们可以顺着梯度的方向改变以增大期望回报。

简单的策略梯度算法

在每一个回合结束后，我们可以就回合中的每一步用以下公式来更新参数，这样的算法称为简单的策略梯度算法：

算法如下

输入：环境，策略

输出：最优策略的估计

参数： 优化器（隐含学习率），折扣因子，控制回合数和回合内步数的参数

1. （初始化）任意值

2.（时序差分更新）对每个回合执行以下操作

2.1（采样）用策略生成轨迹

2.2（初始化回报）

2.3 对t=T-1, T-2,...,0，执行以下步骤：

2.3.1（更新回报）

2.3.2（更新策略）更新以减小, 如

车杆平衡案例

以Gym库的车杆平稳问题为例，一个小车在直线滑轨上移动，一个杆一头连着小车，一头悬空。小车的初始位置和杆的初始角度都是在一定范围内随机选取的。智能体可以控制小车沿着滑轨左右移动。当出现以下任意一种情形时，回合结束：

1. 杆的倾斜角度超过12度

2. 小车移动超过2.4个单位长度

3. 回合到达200步

每进行一步得到1个单位的奖励。我们希望回合能够尽量地长。一般认为，如果在连续的100个回合中的平均奖励>=195，就认为问题解决了。

下面视频是以随机策略来进行，可以看到回合进行到21步就结束了，因为杆的倾斜角度超过了12度。

CartPole_random_trim

我们用策略梯度算法来解决这个问题，如以下的代码：

import gym
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow.keras as keras
from keras.initializers import GlorotUniform
import tqdm
%matplotlib inline
from IPython import display

env = gym.make("CartPole-v0")

class VPGAgent:
    def __init__(self, env, policy_kwargs, baseline_kwargs=None, gamma=0.99):
        self.action_n = env.action_space.n
        self.gamma = gamma
        
        self.trajectory = []
        self.policy_net = self.build_network(
            output_size=self.action_n, 
            output_activation=tf.nn.softmax, 
            loss=keras.losses.categorical_crossentropy, 
            **policy_kwargs)
        if baseline_kwargs:
            self.baseline_net = self.build_network(
                output_size=1,
                **baseline_kwargs)
    
    def build_network(self, hidden_sizes, output_size, activation=tf.nn.relu, output_activation=None, loss=keras.losses.mse, learning_rate=0.01):
        model = keras.Sequential()
        for hidden_size in hidden_sizes:
            model.add(keras.layers.Dense(units=hidden_size, activation=activation))
        model.add(keras.layers.Dense(units=output_size, activation=output_activation))
        optimizer = keras.optimizers.Adam(learning_rate)
        model.compile(optimizer=optimizer, loss=loss)
        return model
    
    def decide(self, observation):
        probs = self.policy_net.predict(observation[np.newaxis])[0]
        action = np.random.choice(self.action_n, p=probs)
        return action
    
    def learn(self, observation, action, reward, done):
        self.trajectory.append((observation, action, reward))
        if done:
            df = pd.DataFrame(self.trajectory, columns=['observation', 'action', 'reward'])
            df['discount'] = self.gamma ** df.index.to_series()
            df['discounted_reward'] = df['discount'] * df['reward']
            df['discounted_return'] = df['discounted_reward'][::-1].cumsum()
            df['psi'] = df['discounted_return']
            
            x = np.stack(df['observation'])
            if hasattr(self, 'baseline_net'):
                df['baseline'] = self.baseline_net.predict(x)
                df['psi'] -= (df['baseline']*df['discount'])
                df['return'] = df['discounted_return']/df['discount']
                y = df['return'].values[:,np.newaxis]
                self.baseline_net.fit(x,y,verbose=0)
                
            sample_weight = df['psi'].values[:, np.newaxis]
            y = np.eye(self.action_n)[df['action']]
            self.policy_net.fit(x,y,sample_weight=sample_weight,verbose=0)
            self.trajectory = []

policy_kwargs = {
    'hidden_sizes': [10,], 
    'activation': tf.nn.relu,
    'learning_rate': 0.01
}
agent = VPGAgent(env, policy_kwargs=policy_kwargs)

def play_montecarlo(env, agent, render=False, train=False, random=False):
    episode_reward = 0
    observation = env.reset()
    step = 0
    img = plt.imshow(env.render(mode='rgb_array'))
    while True:
        step += 1
        if render:
            plt.title("%s | Step: %d" % ("Moutain Car",step))
            plt.axis('off')
            img.set_data(env.render(mode='rgb_array'))
            display.display(plt.gcf())
            display.clear_output(wait=True)
        if random:
            action = np.random.choice(agent.action_n)
        else:
            action = agent.decide(observation)
        next_observation, reward, done, _ = env.step(action)
        episode_reward += reward
        if train:
            agent.learn(observation, action, reward, done)
        if done:
            break
        observation = next_observation
    return episode_reward

episodes = 500
episode_rewards = []
for episode in tqdm.trange(episodes):
    episode_reward = play_montecarlo(env, agent, train=True)
    episode_rewards.append(episode_reward)
plt.plot(episode_rewards)

解释一下代码中的learn函数：

考虑一个回合总共进行了5步，每步的奖励值是1，Gamma是0.9，则：

对应代码中的

discounted_reward = [1, 1*0.9, 1*0.9**2, 1*0.9**3, 1*0.9**4]
discounted_return = [(1+1*0.9+...+1*0.9**4),(1*0.9+...+1*0.9**4),(1*0.9**2+...+1*0.9**4),(1*0.9**3+1*0.9**4),1*0.9**4]

可见discounted_return存储的是的值

对于神经网络的输出函数是softmax，代表不同类型action的概率值。采用交叉熵作为损失函数，其公式为-ylna, a为softmax的输出值。

根据上面策略梯度算法提到的，我们的目标是更新以减小，即交叉熵的损失函数的值乘以，我们只需要在训练神经网络的fit函数中指定sample_weight为即可。

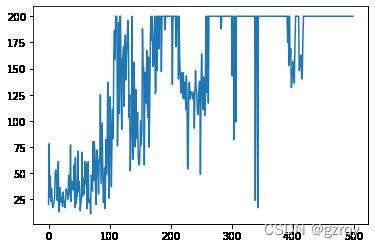
训练500步之后，每个回合的奖励值如下图，可见随着训练的回合数增加，策略逐渐得到了优化，后期很多回合的奖励值都去到了200：

 我们可以用训练好的模型来试玩一个回合，运行以下代码：

episode_reward = play_montecarlo(env, agent, render=True, train=False, random=False)

结果如以下视频：

CartPole_train_Trim