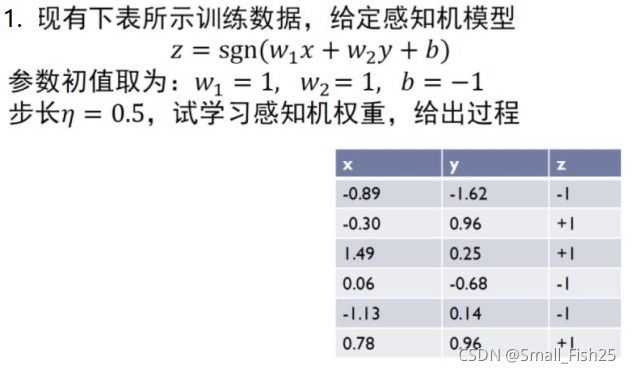
感知机学习总结及例题(附代码及手算过程)

感知机是一种二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，+1代表正类，-1代表负类，是神经网络和支持向量机的基础。

例如一个典型的二分类问题：银行卡申请问题，对于顾客，决定是否给予信用卡

对于一个顾客的信息（年龄、薪资、当前债务等等），我们可以用一个向量表示。然后每个信息条目（维度）均对是否给他信用卡有着正面或者负面的影响，决定我们是否给他信用卡。我们把这些维度加权叠加计算出来，结果若大于某个阈值就给，否则就不给。

设$X=(x_1,x_2,...,x_d)$表示客人的信息，$W=(w_1,w_2,...,w_d)$代表对应的权重系数。则：
$$\{\begin{array}{ll}给,& \text{if }{\sum }_{i=1}^d{w}_i{x}_i>threshold\\ 不给,& \text{if }{\sum }_{i=1}^d{w}_i{x}_i<threshold\end{array}$$
上式子还可以写成：
$$\begin{array}{rl}h(x)& =sign((\sum _{i=1}^d{w}_i{x}_i)-threshold)\\ & =sign((\sum _{i=1}^d{w}_i{x}_i)+(-threshold)\ast (+1))\\ & =sign(\sum _{i=0}^d{w}_i{x}_i)\\ & =sign(w^{T}x)\end{array}$$
这样就可以看成是二个向量的内积再套一个sign函数。

感知机的学习策略：

假设样本线性可分，感知机学习的目标就是求能将正负样本完全分开的分离超平面,即要寻找w，b(因为$wx+b=0$确定了分离超平面)。因此我们需要确定一个学习策略，即定义损失函数，并通过训练样本使其最小化。

损失函数的一个自然选择是误分类点的总数，但是，通过这种方式定义的损失函数对参数w,b来说不是连续可导函数，不易于优化。所有感知机采取的是误分类点到超平面S的总距离。损失函数的推到如下：

设训练集为$T=\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n),\}$，其中$x_i$就相当于我们示例中的客人信息(特征向量)，$y_i$代表是否给信用卡(-1或+1)。则任意点$x_i$到超平面的距离为$d=\frac{w\ast x_i+b}{||w||}$

设超平面S的误分类点集合为M，则误分类点到S的总距离为：
$$\begin{array}{rl}s& =-\frac{1}{||w||}\sum _{x_i\in M}{y}_i\ast (w\ast x_i+b)\\ & =-\sum _{x_i\in M}{y}_i\ast (w\ast x_i+b),\frac{1}{||w||}\text{可忽略}\end{array}$$
感知机学习问题转化为求解上述损失函数的最优化问题，这里可以通过随机梯度下降法来求解。

1. 首先，任意选取一个超平面，然后用梯度下降法不断地极小化目标函数(损失函数)$minL(w,b)=-{\sum }_{x_i\in M}{y}_i\ast (w\ast x_i+b)$。极小化过程中一次随机选取一个误分类点使其梯度下降。

2. 随机梯度下降：

   1. 对w求偏导：$\nabla w \ L(w,b) = - \sum_{x_i\in M} y_i * x_i $

   2. 对b求偏导：$\nabla bL(w,b)=-{\sum }_{x_i\in M}{y}_i$

   3. 更新w,b
      $$\begin{gathered} w⟸w-\eta \ast (-y_i\ast x_i) \\ b⟸b-\eta \ast (-y_i) \end{gathered}$$

3. 判断是否还有误分类点，有则继续，没有则训练结束

举个例子，这个是上课老师布置的作业题目，我们解决下:

方法一：直接Python 冲了它

import numpy as np
import matplotlib.pyplot as plt
import random

# 符号函数
def sign(v):
    if v >= 0:
        return 1
    else:
        return -1

def train(train_num, train_data, lr=0.5):  # 原始训练部分
    w = [1., 1.]  # 初始化权重向量和偏置
    b = -1
    for i in range(train_num):
        #x = random.choice(train_data)
        for x in train_data:
            x1, x2, y = x
            if y * sign(x1 * w[0] + x2 * w[1] + b) <= 0:
                w[0] += lr * y * x1
                w[1] += lr * y * x2
                b += lr * y
                #print(w,b)
    return w, b

# 画散点图
def plot_points(train_data, w, b):
    plt.figure()
    x1 = np.linspace(-1.5, 1.5, 100)
    x2 = (-b - w[0] * x1) / w[1]  # 化简 w1*x1 + w2*x2 + b =0 此时x2相当于竖轴坐标
    plt.plot(x1, x2, color='r', label='y1 data')
    datas_len = len(train_data)
    for i in range(datas_len):
        if train_data[i][-1] == 1:
            plt.scatter(train_data[i][0], train_data[i][1], s=50)
        else:
            plt.scatter(train_data[i][0], train_data[i][1], marker='x', s=50)
    plt.show()

if __name__ == '__main__':
    train_data1 = [[-0.30,0.96,1],[1.49,0.25,1],[0.78,0.96,1]]  # 正样本
    train_data2 = [[-0.89,-1.62,-1], [0.06,-0.68,-1],[-1.13,0.14,-1]]  # 负样本
    data_set = train_data1 + train_data2  # 样本集
    w, b = train(100, data_set, 0.5)  # lr 学习率
    plot_points(data_set, w, b)

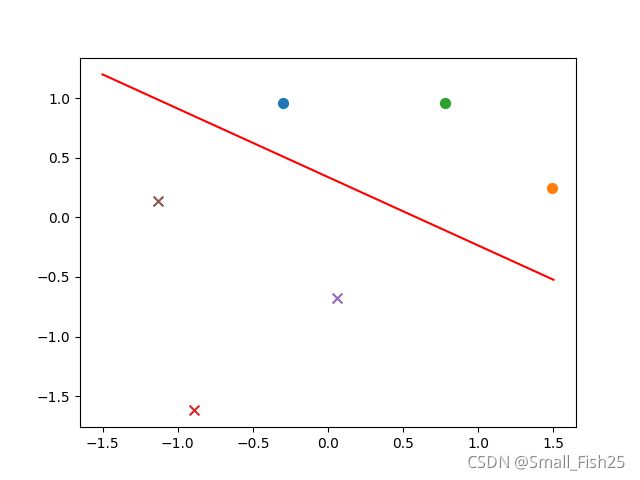
结果如下：

输出$w=(0.85,1.48)b=-0.5$

方法二： 手算呗…

已知初值$w=(1,1)b=-1$，分别待入样本，当$x=-0.3,y=0.96$时不符合，则更新$w和b$
$$\begin{gathered} w=w+\eta (-0.3,0.96)=(0.85,1.48) \\ b=b+\eta \ast (+1)=-0.5 \end{gathered}$$
之后，继续进行训练，此时可能数据比较好，均通过了训练。训练结束…