永磁同步电机控制笔记:电机参数离线辨识方法
文章目录
- 概述
- 1、定子电阻离线辨识
-
- 1.1、定子电阻离线辨识原理
- 1.2、定子电阻离线辨识的误差来源及补偿方法
- 1.3、电阻离线辨识的具体方法
-
- 方法一
- 方法二
- 2、定子电感离线辨识
-
- 2.1、定子电感离线辨识原理
-
- 2.1.1 输入阶跃电压
- 2.1.2 输入脉冲电压
- 2.1.3 输入高频电压
- 2.2、电感辨识的具体方法及误差来源
-
- 2.2.1、零状态响应法
- 2.2.2、斜率法
- 2.2.3、高频电压法
- 3、永磁体磁链辨识
-
- 3.1、永磁体磁链常数辨识原理及方法
- 3.2、永磁体磁链常数辨识仿真验证
- 3.3、小结
概述
永磁同步电机在使用转子磁场定向(foc)方式控制时,需要根据电机的基波模型计算电机转子位置,计算过程中需要依赖电机的定子电阻,定子等效电感,永磁体磁链常数。虽然这几个参数容易测量(测量方法在博主文章永磁同步电机控制笔记:永磁同步电机电阻电感磁链常数的测量方法中进行了简介),但是在一些特殊场合并不便于仪器测量,所以有必要研究使用驱动器进行电机参数辨识的方法。
1、定子电阻离线辨识
定子电阻离线辨识的原理比较简单,但是想要实现准确的定子电阻离线辨识依然不容易。
1.1、定子电阻离线辨识原理
根据欧姆定律,有 R = U / I
显然,使用逆变器发出恒定电压,测量反馈电流即可计算定子电阻。
1.2、定子电阻离线辨识的误差来源及补偿方法
一般来说,相同额定电压下,电机功率越大,额定电流越大,定子电阻越小。电机静止时,逆变器的输出电压全部加在电机的线圈上,想要达到电机的额定电流需要的电压很小。
以一款额定电压50V,额定功率3kw的永磁同步电机为例。额定电流80A,电机定子电阻10毫欧。
理论上只需要0.8V电压,即达到额定电流。因为开关管死区的存在,在输出较小电压时,逆变器输出存在严重的失真。为了获得实际给到线圈的电压,应该尽可能的使用相电压采样电压,而不是给定电压。对于没有相电压采样功能的驱动器,有必要通过死区补偿抵消死区产生的失真。
另外,驱动器无法输出连续的模拟量,其输出为占空比可调的方波,即使电感对电流有一定的滤波能力,但是也无法得到真正的直流电流。

实际的电流响应如上图波形。
为了尽可能的减少电流采样带来的误差,要求每个开关周期在同样的时刻采样电流。并对电流采样结果进行低通滤波。
1.3、电阻离线辨识的具体方法
方法一
1、U相上桥打开,V相下桥打开,W相上下桥均保持关断。采集V相电流。
2、逐渐增加U相上桥,V相下桥打开时间,等待V相电流达到额定电流的1/2
3、保持步骤2占空比,采集此时的电流和电压,并分别低通滤波。
4、等待一定时间后,记录滤波后的电流Iuv和电压值Uuv。
5、计算相电阻为Rs = Uuv/Iuv
6、为了增加电阻辨识精度,可以重复1-5三次,分别发U->V,U->W,V->W电压。测量三次电阻取平均值。
方法二
1、设置电压矢量角度为0(或其他恒定值)。令Vd = 0,Vq = 0,通过svpwm输出。
2、将采样到的相电流进行clark变换,计算Is = sqrt(Iα2 + Iβ2)
3、逐渐增加Vd幅值,等待Is达到1/2额定电流。
4、保持步骤3的Vd幅值,采集此时的电流和电压,并分别低通滤波。
5、等待一定时间后,记录滤波后的电流Is和电压值Vd。
6、计算相电阻Rs = Vd/Is
方法一虽然能够准确测量相电阻,但是需要频繁改变寄存器,控制电流的方向。方法二能够避免操作寄存器,容易在不同的控制器之间移植。
方法二需要用到坐标变换,svpwm调制,计算量大,但是所用到的模块和foc控制所用到的一致,可以直接复用foc代码。
2、定子电感离线辨识
2.1、定子电感离线辨识原理
观察在几种不同电压激励信号下LR电路的相应
2.1.1 输入阶跃电压
LR电路可以看作RC电路的镜像电路。
对LR电路施加阶跃电压,电路的电流波形和对RC电路施加阶跃电流对应的电压波形一致。

对LR电路施加阶跃电压,LR电路的0状态响应如上图。
t = L/R时,电流上升到稳态电流的0.632倍。
稳态电流Iinf = U/R
对定子线圈施加阶跃电压,记录一系列足够密集的电流采样点。找到电流上升到0.632倍Iinf所需时间,测量稳态电流Iinf可以计算定子电阻Rs定子电感Ls
2.1.2 输入脉冲电压

根据电感公式 U = di/dt * L
给定时间为Δt,幅度为Udc的电压脉冲,其中Δt非常小,LR电路时间常数的1/10以下。
此时电流以恒定斜率上升,斜率为Udc/L(忽略电阻压降,也可以看作LR电路0状态相应的起始段)。
测量斜率,可以计算电感。
2.1.3 输入高频电压
电感电流向量图如下,电感电流滞后电压90°,电阻电流和电压相位相同。对于LR串联电路,电流和电压之间的相位差取决于电阻和电感在输入电压频率下的阻抗比例
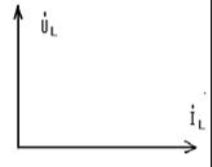
当输入电压矢量Uω频率无限高的时候,电流和电压相位无限接近90°,因为此时电感感抗无穷大,电流幅度无限小。随着Uω频率降低,电流和电压之间相位逐渐减小,电流逐渐变大。

根据上述关系,如果LR电路电阻阻值已知,测量电压电流之间相位差,或者测量电流电压幅度均可以算出电感大小。测量电压电流幅度和相位差,可以同时算得LR电路电感和电阻。
2.2、电感辨识的具体方法及误差来源
本节假设定子电阻已经测得,根据2.1节理论,分析在电机驱动器上可行的电感测量方法。并分析各方法的优缺点和误差来源。
2.2.1、零状态响应法
根据2.1.1,逆变器输出固定脉宽的方波,测量零状态响应。
1、U相上桥开,V相下桥开,其余桥臂关断。发U相到V相电压,W相悬空。使能定时器,令等效电压Uuv = Irate * Rs,其中Irate为电机额定电流,Rs为相电阻
2、高速采集V相电流,并记录每一次触发电流采样时定时器计数值。等到电流稳定时,停止记录。
3、根据记录的电流和采样时刻,拟合指数曲线。
4、计算电流达到0.632倍稳态电流所用时间t0.632
5、Luv = 2Rs * t0.632
重复1-5测量Luw,Lvw
该方法能够同时测量电阻电感,并且容易计算任意两相之间电感,进而计算交直轴Ld,Lq。但是对采样率要求高,计算量大,不容易准确计算出电感大小。而且需要进行较多的寄存器配置。
2.2.2、斜率法
根据2.1.2,逆变器输出Δt为1/20 L/R到1/10L/R之间的脉冲,测量电流斜率。
1、U相上桥开,V相下桥开,其余桥臂关断。发U相到V相电压,W相悬空。使能定时器。
2、触发V相电流采样,并记录触发电流采样时定时器计数值。
3、等待Δt时间后,重复步骤2
4、根据两次电流和时间记录结果计算电流斜率。
5、Luv = Udc / (di/dt)
重复1-5测量Luw,Lvw
该方法能够同时测量电阻电感,并且容易计算任意两相之间电感,进而计算交直轴Ld,Lq。但是不容易补偿电阻压降,逆变器压降。计算结果存在略微误差。同样,该方法需要频繁操作寄存器。
2.2.3、高频电压法
根据2.1.3,逆变器输出高频电压,计算电流的幅度或者电压电流相位可以计算电感。
该需要用到坐标变换,svpwm调制,计算量大,但是所用到的模块和foc控制所用到的一致,可以直接复用foc代码。但是该方法不容易区分交直轴Ld,Lq,更适合表贴式电机
3、永磁体磁链辨识
目前为止大多数永磁体磁链常数辨识的方法都需要电机旋转,几乎没有人能够在电机静止状态下准确辨识永磁体磁链。
3.1、永磁体磁链常数辨识原理及方法
根据永磁同步电机数学模型
v α = R s i α + d ϕ α d t v_{\alpha} = R_s i_{\alpha} + \frac{d \phi _{\alpha}}{dt}\\ vα=Rsiα+dtdϕα
v β = R s i β + d ϕ β d t v_{\beta} = R_s i_{\beta} + \frac{d \phi _{\beta}}{dt}\\ vβ=Rsiβ+dtdϕβ
式中 ϕ α \phi _{\alpha} ϕα为 α \alpha α轴磁链, ϕ β \phi _{\beta} ϕβ为 β \beta β轴磁链。
对于表贴式永磁同步电机,忽略Ld,Lq差异,有
ϕ α = L s i α + ϕ f c o s ( θ ) \phi _{\alpha} = L_s i_{\alpha} + \phi _f cos(\theta) ϕα=Lsiα+ϕfcos(θ)
ϕ β = L s i β + ϕ f s i n ( θ ) \phi _{\beta} = L_s i_{\beta} + \phi _f sin(\theta) ϕβ=Lsiβ+ϕfsin(θ)
式中, ϕ f \phi _f ϕf为永磁体磁链, L s L_s Ls为相电感
d ϕ α d t = v α − R s i α \frac{d \phi _{\alpha}}{dt} = v_{\alpha} - R_s i_{\alpha}\\ dtdϕα=vα−Rsiα
d ϕ β d t = v β − R s i β \frac{d \phi _{\beta}}{dt} = v_{\beta} - R_s i_{\beta}\\ dtdϕβ=vβ−Rsiβ
通过电压可以很容易得到Φα,Φβ的微分。
d ϕ α d t \frac{d \phi _{\alpha}}{dt} dtdϕα d ϕ β d t \frac{d \phi _{\beta}}{dt} dtdϕβ 积分得到 ϕ α \phi _{\alpha} ϕα , ϕ β \phi _{\beta} ϕβ
ϕ f c o s ( θ ) = ϕ α − L s i α \phi _f cos(\theta) = \phi _{\alpha} - L_s i_{\alpha} ϕfcos(θ)=ϕα−Lsiα
ϕ f s i n ( θ ) = ϕ β − L s i β \phi _f sin(\theta) = \phi _{\beta} - L_s i_{\beta} ϕfsin(θ)=ϕβ−Lsiβ
ϕ f = ϕ f c o s ( θ ) 2 + ϕ f s i n ( θ ) 2 \phi _f = \sqrt{\phi _f cos(\theta) ^2 + \phi _f sin(\theta) ^2} ϕf=ϕfcos(θ)2+ϕfsin(θ)2
至此可以计算出永磁体磁链。
需要注意的是,通过对电压积分计算 Φα,Φβ时,因为积分漂移的原因,需要加一个高通滤波器。
3.2、永磁体磁链常数辨识仿真验证
3.3、小结
上述磁链常数辨识方法不需要知道电机的转速,不需要电机的转子位置准确。该方法除了可以用于磁链常数离线辨识,也可以用于磁链常数在线辨识。
也有其他方法根据dq坐标系下的电机模型,实现磁链常数辨识,但是需要转子位置准确,或转速准确。此处不再赘述。