Python实现VRP常见求解算法——自适应大邻域搜索算法（ALNS）

基于python语言，实现经典自适应大邻域搜索算法（ALNS）对车辆路径规划问题（CVRP）进行求解。

优质资源

• python实现6种智能算法求解CVRP问题
• python实现7种智能算法求解MDVRP问题
• python实现7种智能算法求解MDVRPTW问题
• Python版MDHFVRPTW问题智能求解算法代码【TS算法】
• Python版MDHFVRPTW问题智能求解算法代码【SA算法】
• Python版MDHFVRPTW问题智能求解算法代码【GA算法】
• Python版MDHFVRPTW问题智能求解算法代码【DPSO算法】
• Python版MDHFVRPTW问题智能求解算法代码【DE算法】
• Python版MDHFVRPTW问题智能求解算法代码【ACO算法】
• Python版HVRP问题智能求解算法代码【GA算法】
• Python版HVRP问题智能求解算法代码【DPSO算法】

1. 适用场景

• 求解CVRP
• 车辆类型单一
• 车辆容量不小于需求节点最大需求
• 单一车辆基地

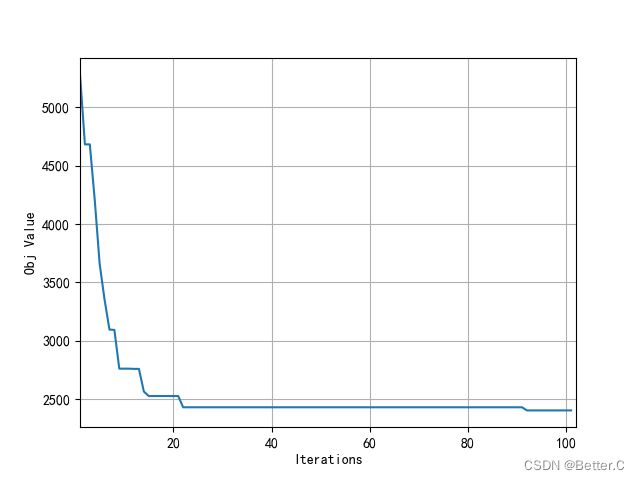
2. 求解效果

（1）收敛曲线

（2）车辆路径

3. 问题分析

CVRP问题的解为一组满足需求节点需求的多个车辆的路径集合。假设某物理网络中共有10个顾客节点，编号为1~10，一个车辆基地，编号为0，在满足车辆容量约束与顾客节点需求约束的条件下，此问题的一个可行解可表示为：[0-1-2-0,0-3-4-5-0,0-6-7-8-0,0-9-10-0]，即需要4个车辆来提供服务，车辆的行驶路线分别为0-1-2-0,0-3-4-5-0,0-6-7-8-0,0-9-10-0。由于车辆的容量固定，基地固定，因此可以将上述问题的解先表示为[1-2-3-4-5-6-7-8-9-10]的有序序列，然后根据车辆的容量约束，对序列进行切割得到若干车辆的行驶路线。因此可以将CVRP问题转换为TSP问题进行求解，得到TSP问题的优化解后再考虑车辆容量约束进行路径切割，得到CVRP问题的解。这样的处理方式可能会影响CVRP问题解的质量，但简化了问题的求解难度。

4. 数据格式

以xlsx文件储存网络数据，其中第一行为标题栏，第二行存放车辆基地数据。在程序中车辆基地seq_no编号为-1，需求节点seq_id从0开始编号。可参考github主页相关文件。

5. 分步实现

（1）数据结构
为便于数据处理，定义Sol()类，Node()类，Model()类，其属性如下表：

• Sol()类，表示一个可行解

属性	描述
nodes_seq	需求节点seq_no有序排列集合，对应TSP的解
obj	优化目标值
routes	车辆路径集合，对应CVRP的解

• Node()类，表示一个网络节点

属性	描述
id	物理节点id，可选
name	物理节点名称，可选
seq_no	物理节点映射id，基地节点为-1，需求节点从0编号
x_coord	物理节点x坐标
y_coord	物理节点y坐标
demand	物理节点需求

• Model()类，存储算法参数

属性	描述
best_sol	全局最优解，值类型为Sol()
node_list	物理节点集合，值类型为Node()
node_seq_no_list	物理节点映射id集合
depot	车辆基地，值类型为Node()
number_of_nodes	需求节点数量
opt_type	优化目标类型，0：最小车辆数，1：最小行驶距离
vehicle_cap	车辆容量
distance	网络弧距离
rand_d_max	随机破坏程度上限
rand_d_min	随机破坏程度下限
worst_d_max	最坏破坏程度上限
worst_d_min	最坏破坏程度下限
regret_n	次优位置个数
r1	算子奖励1
r2	算子奖励2
r3	算子奖励3
rho	算子权重衰减系数
d_weight	破坏算子权重
d_select	破坏算子被选中次数/每轮
d_score	破坏算子被奖励得分/每轮
d_history_select	破坏算子历史共计被选中次数
d_history_score	破坏算子历史共计被奖励得分
r_weight	修复算子权重
r_select	修复算子被选中次数/每轮
r_score	修复算子被奖励得分/每轮
r_history_select	修复算子历史共计被选中次数
r_history_score	修复算子历史共计被奖励得分
（2）文件读取

def readXlsxFile(filepath,model):
    # It is recommended that the vehicle depot data be placed in the first line of xlsx file
    node_seq_no = -1#the depot node seq_no is -1,and demand node seq_no is 0,1,2,...
    df = pd.read_excel(filepath)
    for i in range(df.shape[0]):
        node=Node()
        node.id=node_seq_no
        node.seq_no=node_seq_no
        node.x_coord= df['x_coord'][i]
        node.y_coord= df['y_coord'][i]
        node.demand=df['demand'][i]
        if df['demand'][i] == 0:
            model.depot=node
        else:
            model.node_list.append(node)
            model.node_seq_no_list.append(node_seq_no)
        try:
            node.name=df['name'][i]
        except:
            pass
        try:
            node.id=df['id'][i]
        except:
            pass
        node_seq_no=node_seq_no+1
    model.number_of_nodes=len(model.node_list)

（3）初始化参数
在初始化参数时计算网络弧距离，以便后续算子使用。

def initParam(model):
    for i in range(model.number_of_nodes):
        for j in range(i+1,model.number_of_nodes):
            d=math.sqrt((model.node_list[i].x_coord-model.node_list[j].x_coord)**2+
                        (model.node_list[i].y_coord-model.node_list[j].y_coord)**2)
            model.distance[i,j]=d
            model.distance[j,i]=d

（4）初始解

def genInitialSol(node_seq):
    node_seq=copy.deepcopy(node_seq)
    random.seed(0)
    random.shuffle(node_seq)
    return node_seq

（5）目标值计算
目标值计算依赖 " splitRoutes " 函数对TSP可行解分割得到车辆行驶路线和所需车辆数， " calDistance " 函数计算行驶距离。

def splitRoutes(nodes_seq,model):
    num_vehicle = 0
    vehicle_routes = []
    route = []
    remained_cap = model.vehicle_cap
    for node_no in nodes_seq:
        if remained_cap - model.node_list[node_no].demand >= 0:
            route.append(node_no)
            remained_cap = remained_cap - model.node_list[node_no].demand
        else:
            vehicle_routes.append(route)
            route = [node_no]
            num_vehicle = num_vehicle + 1
            remained_cap =model.vehicle_cap - model.node_list[node_no].demand
    vehicle_routes.append(route)
    return num_vehicle,vehicle_routes
def calDistance(route,model):
    distance=0
    depot=model.depot
    for i in range(len(route)-1):
        distance+=model.distance[route[i],route[i+1]]
    first_node=model.node_list[route[0]]
    last_node=model.node_list[route[-1]]
    distance+=math.sqrt((depot.x_coord-first_node.x_coord)**2+(depot.y_coord-first_node.y_coord)**2)
    distance+=math.sqrt((depot.x_coord-last_node.x_coord)**2+(depot.y_coord - last_node.y_coord)**2)
    return distance
def calObj(nodes_seq,model):
    num_vehicle, vehicle_routes = splitRoutes(nodes_seq, model)
    if model.opt_type==0:
        return num_vehicle,vehicle_routes
    else:
        distance=0
        for route in vehicle_routes:
            distance+=calDistance(route,model)
        return distance,vehicle_routes

（6）定义destroy算子（破坏算子）
这里实现两种destory：

• random destroy : 随机从当前解中移除一定比例的需求节点
• worst destroy：从当前解中移除一定比例引起目标函数增幅较大的需求节点

# define random destory action
def createRandomDestory(model):
    d=random.uniform(model.rand_d_min,model.rand_d_max)
    reomve_list=random.sample(range(model.number_of_nodes),int(d*model.number_of_nodes))
    return reomve_list
# define worse destory action
def createWorseDestory(model,sol):
    deta_f=[]
    for node_no in sol.nodes_seq:
        nodes_seq_=copy.deepcopy(sol.nodes_seq)
        nodes_seq_.remove(node_no)
        obj,vehicle_routes=calObj(nodes_seq_,model)
        deta_f.append(sol.obj-obj)
    sorted_id = sorted(range(len(deta_f)), key=lambda k: deta_f[k], reverse=True)
    d=random.randint(model.worst_d_min,model.worst_d_max)
    remove_list=sorted_id[:d]
    return remove_list

（7）定义repair算子（修复算子）
这里实现三种repair：

• random repair ：将被移除的需求节点随机插入已分配节点序列中；
• greedy repair ：根据被移除的需求节点插入已分配节点序列中每个可能位置的目标函数增量大小，依次选择目标函数增量最小的需求节点与插入位置组合，直到所有被移除的需求节点都重新插入为止（可简单理解为，依次选择使目标函数增量最小的需求节点与其最优的插入位置）；
  $$argmi{n}_{p\in P,i\in IP}f(s_{p,i})$$
  其中，$P$为未分配的需求节点集合，$IP$为可能插入的位置集合，$f(s_{p,i})$为将需求节点$p$插入$s$中第$i$个位置时的目标函数值。
• regret repair：计算被移除节点插回到已分配节点序列中n个次优位置时其目标函数值与最优位置的目标函数值的差之和，然后选择差之和最大的需求节点及其最优位置。（可简单理解为，优先选择n个次优位置与最优位置距离较远的需求节点及其最优位置。）；
  $$argma{x}_{p\in P}\left\{{\sum }_{i=2}^n(f(s_i(p))-f(s_1(p)))\right\}$$
  其中，$P$为未分配的需求节点集合，$f(s_i(p))-f(s_1(p))$为将需求节点$p$插入$s$中最优位置和第$i$次优位置时目标函数差值。

def createRandomRepair(remove_list,model,sol):
    unassigned_nodes_seq=[]
    assigned_nodes_seq = []
    # remove node from current solution
    for i in range(model.number_of_nodes):
        if i in remove_list:
            unassigned_nodes_seq.append(sol.nodes_seq[i])
        else:
            assigned_nodes_seq.append(sol.nodes_seq[i])
    # insert
    for node_no in unassigned_nodes_seq:
        index=random.randint(0,len(assigned_nodes_seq)-1)
        assigned_nodes_seq.insert(index,node_no)
    new_sol=Sol()
    new_sol.nodes_seq=copy.deepcopy(assigned_nodes_seq)
    new_sol.obj,new_sol.routes=calObj(assigned_nodes_seq,model)
    return new_sol

def createGreedyRepair(remove_list,model,sol):
    unassigned_nodes_seq = []
    assigned_nodes_seq = []
    # remove node from current solution
    for i in range(model.number_of_nodes):
        if i in remove_list:
            unassigned_nodes_seq.append(sol.nodes_seq[i])
        else:
            assigned_nodes_seq.append(sol.nodes_seq[i])
    #insert
    while len(unassigned_nodes_seq)>0:
        insert_node_no,insert_index=findGreedyInsert(unassigned_nodes_seq,assigned_nodes_seq,model)
        assigned_nodes_seq.insert(insert_index,insert_node_no)
        unassigned_nodes_seq.remove(insert_node_no)
    new_sol=Sol()
    new_sol.nodes_seq=copy.deepcopy(assigned_nodes_seq)
    new_sol.obj,new_sol.routes=calObj(assigned_nodes_seq,model)
    return new_sol

def findGreedyInsert(unassigned_nodes_seq,assigned_nodes_seq,model):
    best_insert_node_no=None
    best_insert_index = None
    best_insert_cost = float('inf')
    assigned_nodes_seq_obj,_=calObj(assigned_nodes_seq,model)
    for node_no in unassigned_nodes_seq:
        for i in range(len(assigned_nodes_seq)):
            assigned_nodes_seq_ = copy.deepcopy(assigned_nodes_seq)
            assigned_nodes_seq_.insert(i, node_no)
            obj_, _ = calObj(assigned_nodes_seq_, model)
            deta_f = obj_ - assigned_nodes_seq_obj
            if deta_f<best_insert_cost:
                best_insert_index=i
                best_insert_node_no=node_no
                best_insert_cost=deta_f
    return best_insert_node_no,best_insert_index

def createRegretRepair(remove_list,model,sol):
    unassigned_nodes_seq = []
    assigned_nodes_seq = []
    # remove node from current solution
    for i in range(model.number_of_nodes):
        if i in remove_list:
            unassigned_nodes_seq.append(sol.nodes_seq[i])
        else:
            assigned_nodes_seq.append(sol.nodes_seq[i])
    # insert
    while len(unassigned_nodes_seq)>0:
        insert_node_no,insert_index=findRegretInsert(unassigned_nodes_seq,assigned_nodes_seq,model)
        assigned_nodes_seq.insert(insert_index,insert_node_no)
        unassigned_nodes_seq.remove(insert_node_no)
    new_sol = Sol()
    new_sol.nodes_seq = copy.deepcopy(assigned_nodes_seq)
    new_sol.obj, new_sol.routes = calObj(assigned_nodes_seq, model)
    return new_sol

def findRegretInsert(unassigned_nodes_seq,assigned_nodes_seq,model):
    opt_insert_node_no = None
    opt_insert_index = None
    opt_insert_cost = -float('inf')
    for node_no in unassigned_nodes_seq:
        n_insert_cost=np.zeros((len(assigned_nodes_seq),3))
        for i in range(len(assigned_nodes_seq)):
            assigned_nodes_seq_=copy.deepcopy(assigned_nodes_seq)
            assigned_nodes_seq_.insert(i,node_no)
            obj_,_=calObj(assigned_nodes_seq_,model)
            n_insert_cost[i,0]=node_no
            n_insert_cost[i,1]=i
            n_insert_cost[i,2]=obj_
        n_insert_cost= n_insert_cost[n_insert_cost[:, 2].argsort()]
        deta_f=0
        for i in range(1,model.regret_n):
            deta_f=deta_f+n_insert_cost[i,2]-n_insert_cost[0,2]
        if deta_f>opt_insert_cost:
            opt_insert_node_no = int(n_insert_cost[0, 0])
            opt_insert_index=int(n_insert_cost[0,1])
            opt_insert_cost=deta_f
    return opt_insert_node_no,opt_insert_index

（8）随机选择算子
采用轮盘赌法选择destory和repair算子。

#select destory action and repair action
def selectDestoryRepair(model):
    d_weight=model.d_weight
    d_cumsumprob = (d_weight / sum(d_weight)).cumsum()
    d_cumsumprob -= np.random.rand()
    destory_id= list(d_cumsumprob > 0).index(True)

    r_weight=model.r_weight
    r_cumsumprob = (r_weight / sum(r_weight)).cumsum()
    r_cumsumprob -= np.random.rand()
    repair_id = list(r_cumsumprob > 0).index(True)
    return destory_id,repair_id

（9）执行destory算子
根据被选择的destory算子返回需要被移除的节点index序列。

# do destory action
def doDestory(destory_id,model,sol):
    if destory_id==0:
        reomve_list=createRandomDestory(model)
    else:
        reomve_list=createWorseDestory(model,sol)
    return reomve_list

（10）执行repair算子
根据被选择的repair算子对当前接进行修复操作。

def doRepair(repair_id,reomve_list,model,sol):
    if repair_id==0:
        new_sol=createRandomRepair(reomve_list,model,sol)
    elif repair_id==1:
        new_sol=createGreedyRepair(reomve_list,model,sol)
    else:
        new_sol=createRegretRepair(reomve_list,model,sol)
    return new_sol

（11）重置算子得分
在每执行pu次destory和repair，重置算子的得分和被选中次数。

# reset action score
def resetScore(model):

    model.d_select = np.zeros(2)
    model.d_score = np.zeros(2)

    model.r_select = np.zeros(3)
    model.r_score = np.zeros(3)

（12）更新算子权重
对于算子权重的更新有两种策略，一种是每执行依次destory和repair更新一次，另一种是每执行pu次destory和repair更新一次权重。前者，能够保证权重及时得到更新，但却需要更多的计算时间；后者，通过合理设置pu参数，节省了计算时间，同时又不至于权重更新太滞后。这里采用后者更新策略。
$$w(h)=\{\begin{array}{cccc}& (1-\rho )w(h)+\rho \frac{s(h)}{u(h)},& if& u(h)>0\\ & (1-\rho )w(h),& if& u(h)=0\end{array}$$
其中，$w(h)$表示算子权重，$\rho$为衰减系数，$s(h)$为算子总奖励得分，$u(h)$为算子被选中次数。

# update action weight
def updateWeight(model):
    for i in range(model.d_weight.shape[0]):
        if model.d_select[i]>0:
            model.d_weight[i]=model.d_weight[i]*(1-model.rho)+model.rho*model.d_score[i]/model.d_select[i]
        else:
            model.d_weight[i] = model.d_weight[i] * (1 - model.rho)
    for i in range(model.r_weight.shape[0]):
        if model.r_select[i]>0:
            model.r_weight[i]=model.r_weight[i]*(1-model.rho)+model.rho*model.r_score[i]/model.r_select[i]
        else:
            model.r_weight[i] = model.r_weight[i] * (1 - model.rho)
    model.d_history_select = model.d_history_select + model.d_select
    model.d_history_score = model.d_history_score + model.d_score
    model.r_history_select = model.r_history_select + model.r_select
    model.r_history_score = model.r_history_score + model.r_score

（13）绘制收敛曲线

def plotObj(obj_list):
    plt.rcParams['font.sans-serif'] = ['SimHei']  #show chinese
    plt.rcParams['axes.unicode_minus'] = False   # Show minus sign
    plt.plot(np.arange(1,len(obj_list)+1),obj_list)
    plt.xlabel('Iterations')
    plt.ylabel('Obj Value')
    plt.grid()
    plt.xlim(1,len(obj_list)+1)
    plt.show()

（14）输出结果

def outPut(model):
    work=xlsxwriter.Workbook('result.xlsx')
    worksheet=work.add_worksheet()
    worksheet.write(0,0,'opt_type')
    worksheet.write(1,0,'obj')
    if model.opt_type==0:
        worksheet.write(0,1,'number of vehicles')
    else:
        worksheet.write(0, 1, 'drive distance of vehicles')
    worksheet.write(1,1,model.best_sol.obj)
    for row,route in enumerate(model.best_sol.routes):
        worksheet.write(row+2,0,'v'+str(row+1))
        r=[str(i)for i in route]
        worksheet.write(row+2,1, '-'.join(r))
    work.close()

（15）主函数
主函数中设置两层循环，外层循环由epochs参数控制，内层循环由pu参数控制，每执行一次内层循环更新一次算子权重。对于邻域新解的接受准则有很多类型，比如RW, GRE,SA,TA,OBA,GDA，这里采用TA准则，即f(newx)-f(x)

def run(filepath,rand_d_max,rand_d_min,worst_d_min,worst_d_max,regret_n,r1,r2,r3,rho,phi,epochs,pu,v_cap,opt_type):
    """
    :param filepath: Xlsx file path
    :param rand_d_max: max degree of random destruction
    :param rand_d_min: min degree of random destruction
    :param worst_d_max: max degree of worst destruction
    :param worst_d_min: min degree of worst destruction
    :param regret_n:  n next cheapest insertions
    :param r1: score if the new solution is the best one found so far.
    :param r2: score if the new solution improves the current solution.
    :param r3: score if the new solution does not improve the current solution, but is accepted.
    :param rho: reaction factor of action weight
    :param phi: the reduction factor of threshold
    :param epochs: Iterations
    :param pu: the frequency of weight adjustment
    :param v_cap: Vehicle capacity
    :param opt_type: Optimization type:0:Minimize the number of vehicles,1:Minimize travel distance
    :return:
    """
    model=Model()
    model.rand_d_max=rand_d_max
    model.rand_d_min=rand_d_min
    model.worst_d_min=worst_d_min
    model.worst_d_max=worst_d_max
    model.regret_n=regret_n
    model.r1=r1
    model.r2=r2
    model.r3=r3
    model.rho=rho
    model.vehicle_cap=v_cap
    model.opt_type=opt_type
    readXlsxFile(filepath, model)
    initParam(model)
    history_best_obj = []
    sol = Sol()
    sol.nodes_seq = genInitialSol(model.node_seq_no_list)
    sol.obj, sol.routes = calObj(sol.nodes_seq, model)
    model.best_sol = copy.deepcopy(sol)
    history_best_obj.append(sol.obj)
    for ep in range(epochs):
        T=sol.obj*0.2
        resetScore(model)
        for k in range(pu):
            destory_id,repair_id=selectDestoryRepair(model)
            model.d_select[destory_id]+=1
            model.r_select[repair_id]+=1
            reomve_list=doDestory(destory_id,model,sol)
            new_sol=doRepair(repair_id,reomve_list,model,sol)
            if new_sol.obj<sol.obj:
                sol=copy.deepcopy(new_sol)
                if new_sol.obj<model.best_sol.obj:
                    model.best_sol=copy.deepcopy(new_sol)
                    model.d_score[destory_id]+=model.r1
                    model.r_score[repair_id]+=model.r1
                else:
                    model.d_score[destory_id]+=model.r2
                    model.r_score[repair_id]+=model.r2
            elif new_sol.obj-sol.obj<T:
                sol=copy.deepcopy(new_sol)
                model.d_score[destory_id] += model.r3
                model.r_score[repair_id] += model.r3
            T=T*phi
            print("%s/%s:%s/%s， best obj: %s" % (ep,epochs,k,pu, model.best_sol.obj))
            history_best_obj.append(model.best_sol.obj)
        updateWeight(model)

    plotObj(history_best_obj)
    outPut(model)
    print("random destory weight is {:.3f}\tselect is {}\tscore is {:.3f}".format(model.d_weight[0],
                                                                        model.d_history_select[0],
                                                                        model.d_history_score[0]))
    print("worse destory weight is {:.3f}\tselect is {}\tscore is {:.3f} ".format(model.d_weight[1],
                                                                        model.d_history_select[1],
                                                                        model.d_history_score[1]))
    print("random repair weight is {:.3f}\tselect is {}\tscore is {:.3f}".format(model.r_weight[0],
                                                                       model.r_history_select[0],
                                                                       model.r_history_score[0]))
    print("greedy repair weight is {:.3f}\tselect is {}\tscore is {:.3f}".format(model.r_weight[1],
                                                                       model.r_history_select[1],
                                                                       model.r_history_score[1]))
    print("regret repair weight is {:.3f}\tselect is {}\tscore is {:.3f}".format(model.r_weight[2],
                                                                       model.r_history_select[2],
                                                                       model.r_history_score[2]))

6. 完整代码

代码和数据文件可获取【私信】：

https://download.csdn.net/download/python_n/37357242

参考

1. https://oparu.uni-ulm.de/xmlui/bitstream/handle/123456789/3264/vts_9568_14474.pdf?sequence=1
2. https://homes.di.unimi.it/righini/Didattica/AlgoritmiEuristici/MaterialeAE/15%20-%20ALNS.pdf
3. https://mp.weixin.qq.com/s/fpeNCKo62d_7gqBnWd2tTw
4. https://mp.weixin.qq.com/s/l7fTHRye4pPBtWrlPrZ6mA
5. https://mp.weixin.qq.com/s/K6EgtMdarCgr_vK4qZfGlw