【附核心代码】C++实现特征值连续的多分类问题(朴素贝叶斯、决策树、感知机)
C++实现简单机器学习算法
- 朴素贝叶斯
-
- 原理
- 核心代码
- 决策树
-
- 原理
- 核心代码
- 感知机
-
- 原理
- 算法流程
- 核心代码
- 总结
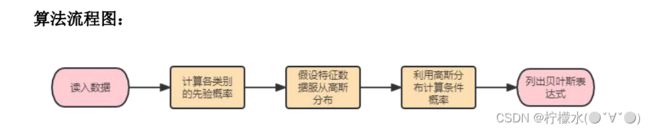
朴素贝叶斯
原理
详细公式及推导请参考博客 朴素贝叶斯
核心代码
//计算先验概率
vector<vector<double>> Probability(vector<vector<double>> train_data) {
vector<vector<double>> p_u;
vector<double> p{ 0,0,0,0 }; //初始化p为3个0
vector<double> u1{ 0,0,0,0 }; //第一列数据的均值,u1[0]表示类别‘0’中第一个特征的均值
vector<double> u2{ 0,0,0,0 };
vector<double> s1{ 0,0,0,0 }; //第一列数据的方差,s1[0]表示类别‘0’中第一个特征的方差
vector<double> s2{ 0,0,0,0 };
int len = train_data.size();
for (int i = 0; i < len; ++i)
{
double a = train_data[i][0];
double b = train_data[i][1];
if (train_data[i][2] == 0)
{
p[0]++;
u1[0] += a;
u2[0] += b;
}
if (train_data[i][2] == 1)
{
p[1]++;
u1[1] += a;
u2[1] += b;
}
if (train_data[i][2] == 2)
{
p[2]++;
u1[2] += a;
u2[2] += b;
}
if (train_data[i][2] == 3)
{
p[3]++;
u1[3] += a;
u2[3] += b;
}
}
for (int i = 0; i < 4; ++i)
{
u1[i] /= p[i];
u2[i] /= p[i];
}
p_u.push_back(p);
p_u.push_back(u1);
p_u.push_back(u2);
//计算sigma
for (int k = 0; k < len; ++k)
{
double a = train_data[k][0];
double b = train_data[k][1];
if (train_data[k][2] == 0)
{
s1[0] += (a - u1[0]) * (a - u1[0]);
s2[0] += (a - u2[0]) * (a - u2[0]);
}
if (train_data[k][2] == 1)
{
s1[1] += (a - u1[1]) * (a - u1[1]);
s2[1] += (a - u2[1]) * (a - u2[1]);
}
if (train_data[k][2] == 2)
{
s1[2] += (a - u1[2]) * (a - u1[2]);
s2[2] += (a - u2[2]) * (a - u2[2]);
}
if (train_data[k][2] == 3)
{
s1[3] += (a - u1[3]) * (a - u1[3]);
s2[3] += (a - u2[3]) * (a - u2[3]);
}
}
for (int k = 0; k < 4; ++k)
{
s1[k] = s1[k] / p[k];
s2[k] = s2[k] / p[k];
}
for (int i = 0; i < 4; ++i) p[i] = (p[i] + 1) / (len + 4);
p_u.push_back(s1);
p_u.push_back(s2);
return p_u;
}
//计算P(x_j|c_i):类别i的情况下特征是x_j的概率
double P_Gauss(double x, double u, double s_f) {
return exp(-(((x - u) * (x - u)) / (2 * s_f))) / sqrt(2 * PI * s_f);
}
决策树
原理
参见 决策树分类原理
这篇文章我受益很多,里面举了具体的例子,强烈推荐大家阅读


核心代码
由于我也是人工智能萌新一枚,以下代码框架是根据python决策树改写而来的,因此有些地方可能略显复杂,但是我秉持着能跑就行的心态,后期也懒得动改了。
类的构造略显单调,能用就行!!!id存的是第几个属性,value是属性的值
class Node {
public:
int id;
double value;
Node* leftBranch;
Node* rightBranch;
Node()
{
this->id = -1;
this->value = -1;
this->leftBranch = NULL;
this->rightBranch = NULL;
}
};
下面主要展示递归构建树的过程以及连续特征是如何划分的
//分割后第0列为小数据,第1列为大数据
vector<vector<vector<double>>> splitDataSet(vector<vector<double>> dataSet, int id, double val) {
vector<vector<vector<double>>> sp;
vector<vector<double>> dataSet_feat;
vector<vector<double>> left;
vector<vector<double>> right;
const int len = dataSet.size();
Order2Sort* s = new Order2Sort[len];
Vec2Stru(s, dataSet);
if (id == 0)
{
sort(s, s + len, cmp1);//对特征1进行升序排列
dataSet_feat = Stru2Vec(s, len);//特征1升序
delete[] s;
}
else if (id == 1)
{
sort(s, s + len, cmp2);//对特征2进行升序排列
dataSet_feat = Stru2Vec(s, len);//特征2升序
delete[] s;
}
else
{
cout << "ERROR IN splitDataSet \"id=-1\"";
exit(1);
}
for (int i = 0; i < len; ++i)
{
if (dataSet_feat[i][id] <= val)
{
left.push_back(dataSet_feat[i]);
}
if (dataSet_feat[i][id] > val)
{
right.push_back(dataSet_feat[i]);
}
}
sp.push_back(left);
sp.push_back(right);
return sp;
}
vector<Node*> MyTrees;
Node* createTree(Node* tree, vector<vector<double>> dataSet) {
const int len = dataSet.size();
vector<double> labels = { 0,0,0,0 };
for (int i = 0; i < len; ++i)
{
if (dataSet[i][2] == 0) labels[0]++;
if (dataSet[i][2] == 1) labels[1]++;
if (dataSet[i][2] == 2) labels[2]++;
if (dataSet[i][2] == 3) labels[3]++;
}
for (int i = 0; i < 4; ++i)
{
if (labels[i] == len)
{
tree->value = i;
return tree;
}
}
vector<vector<double>> mid_numVec = get_MidnumVec(dataSet);
Feat_Id fd = chooseBestFeatureToSplit(dataSet, mid_numVec);
tree->id = fd.id;
tree->value = fd.feature;
//cout << "feature=" << fd.feature << " id=" << fd.id << endl;
vector<vector<vector<double>>> sp = splitDataSet(dataSet, fd.id, fd.feature);
vector<vector<double>> left = sp.at(0);
vector<vector<double>> right = sp.at(1);
MyTrees.push_back(new Node());
tree->leftBranch = createTree(MyTrees.back(), left);
MyTrees.push_back(new Node());
tree->rightBranch = createTree(MyTrees.back(), right);
return tree;
}
感知机
原理
详细公式及推导推荐参考博客感知机
算法流程
不知道大家看了上面那个博客没有,我在这提醒一下,上面博客中的多分类情况的适用范围是多分类线性可分的情况(我的理解大概是这样的,就是说把某一个类别看成类别1,其他类别全看成类别-1,这个二分类是线性可分的),下面我们打印出的数据集分布情况可以看出红色于其他数据是非 线性可分的,所以直接用该方法行不通 跳坑的我 亲测该算法训练了一万轮也没出结果,而且权重越来越怪异,静下心来把原理理了一边才发现问题所在 菜狗本狗一枚
由于perceptron对训练集数据是否线性可分有严格要求,在处理非线性可分的数据集时往往需要通过核函数来处理。正如“二”中所介绍,我将采用进行多次二分类的方法来完成多分类任务,那么我首先需要知道训练集大致的分布情况以决定是否需要使用核函数,通过以下matlab代码可以轻松生成训练集的分布情况,我们发现数据集两两之间是线性可分的,虽然“类别0”和“类别1”有一定的重叠区,但考虑到那仅仅是极小的一部分数据,对整体预测效果的影响不大,我们可以近似认为它也是线性可分的。

流程图:
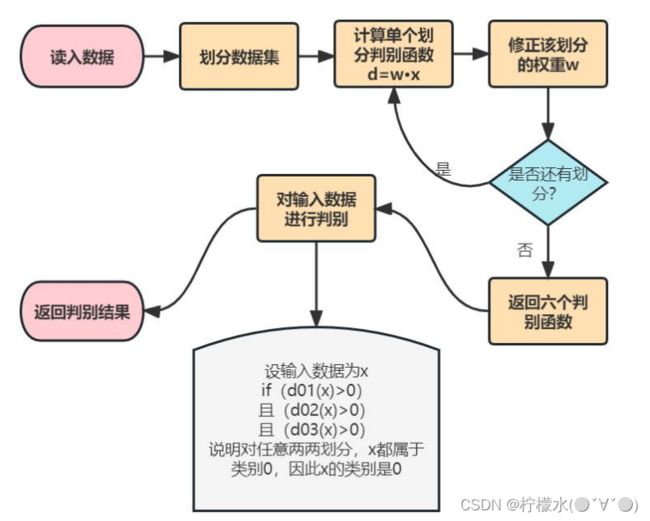
核心代码
double distance(vector<double> w, vector<double> x) {
if (x.size() == 2) x.push_back(1); //该行用于测试集,因为测试集仅两列,补充此行代码可简化后续测试
double wx = (w[0] * x[0] + w[1] * x[1] + w[2]) * x[2];
return wx;
}
double yita = 1;
void SGD(vector<double>& w, vector<double>x) {
double c = yita * x[2];
w[0] += c * x[0];
w[1] += c * x[1];
w[2] += c;
}
int cnt = 0;
//数据传的是哪两类的,w就传入对应的类别。 如dataSet传data01,则w传w01,clus传0(表示类别0为正例)
bool updata(vector<vector<double>> dataSet, vector<double>& w, int clus) {
printf("第%d轮迭代……\n", ++cnt);
bool signal = true;
int len = dataSet.size();
for (int i = 0; i < len; ++i)
{
int cluster = dataSet[i][2];
vector<double> tempX = dataSet[i];
if (cluster == clus) tempX[2] = 1;
else tempX[2] = -1;
double w_x = distance(w, tempX);
if (w_x > 0) continue;
else
{
SGD(w, tempX);
signal = false;
}
}
printf("本轮权重:%lf\t%lf\t%lf\n", w[0], w[1], w[2]);
return signal;
}
// 0 1 2 3 4 5
//01 02 03 12 13 23
int selectCluster(vector<vector<double>> ww, vector<double> testx) {
if (distance(ww[0], testx) > 0 && distance(ww[1], testx) > 0 && distance(ww[2], testx) > 0)
return 0;
if (distance(ww[0], testx) <= 0 && distance(ww[3], testx) > 0 && distance(ww[4], testx) > 0)
return 1;
if (distance(ww[1], testx) <= 0 && distance(ww[3], testx) <= 0 && distance(ww[5], testx) > 0)
return 2;
if (distance(ww[2], testx) <= 0 && distance(ww[4], testx) <= 0 && distance(ww[5], testx) <= 0)
return 3;
else
{
cout << "selectCluster()函数中止" << endl;
return -1;
}
}
总结
第一次写博客,写的不好的地方望谅解