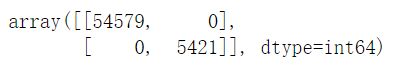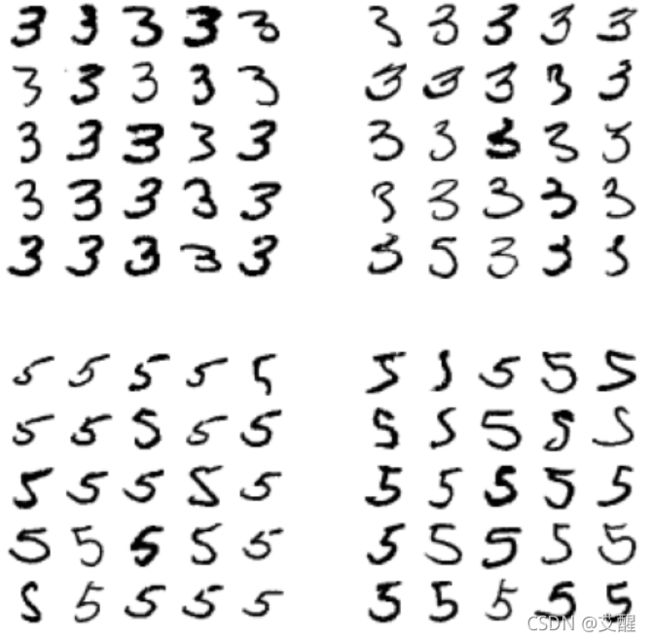多种分类以及模型评估
多种分类以及模型评估
- 分类
-
- 获取mnist数据集
- 获取训练数据和标签
- 数据标准化及数据集划分
- 训练二分类器
-
- 划分数据集
- 随机梯度下降分类
- 性能测试
-
- 使用交叉验证测量准确率
- 傻瓜版分类器
- 混淆矩阵
-
- 随机梯度下降分类器对应的混淆矩阵
- 混淆矩阵最佳状态
- 精度和召回率
-
- 精度/召回率权衡
- 阈值为0的情况
- 阈值为8000的情况
- 阈值对精度和召回率影响变化图像
- 确定阈值
- ROC曲线
-
- 测试精度和召回率
- 多类分类器
-
- OvR与OvO
- 随机梯度下降和随机森林
- 误差分析
- 3和5误判的情况
- 多标签分类
- 多输出分类
分类
获取mnist数据集
from sklearn.datasets import fetch_openml
import numpy as np
mnist = fetch_openml('mnist_784', version=1)
mnist.keys()
运行结果：
其中：
DESCR:描述数据集
data:包含一个数组，每个实例一行，每个特征一列
target:包含一个带标记的数组
获取训练数据和标签
X, y = mnist['data'], mnist['target']
import matplotlib.pyplot as plt
import matplotlib as mpl
some_digit = np.array(X)[0]
some_digit_image = some_digit.reshape(28, 28)
plt.imshow(some_digit_image, cmap="binary")
plt.axis("off")
plt.show()
显示第0个图片
数据标准化及数据集划分
因为标签是字符型的，现在将字符型转换成无符号8位整型
y = y.astype(np.uint8)
mnist数据集已经分好了训练集（前60000）和测试集（后10000）这里直接分离就行
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
训练二分类器
划分数据集
这里是将原来的0-9数据集按照5或非5进行划分
y_train_5 = (y_train == 5) # 是5为1，非5为0
y_test_5 = (y_test == 5)
随机梯度下降分类
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(random_state=42) # random_state=42是将随机值设置为42,这里也可以换做其他数值
sgd_clf.fit(X_train, y_train_5) # 训练
sgd_clf.predict([some_digit]) # some_digit这个图片是之前plot的那个5的图片
运行结果：
性能测试
使用交叉验证测量准确率
k折分层抽样：
from sklearn.model_selection import StratifiedKFold # K折分层抽样
from sklearn.base import clone
skfolds = StratifiedKFold(n_splits=3) # 分成3折
for train_index, test_index in skfolds.split(X_train, y_train_5): # 这还是那个5和非5的分类器
clone_clf = clone(sgd_clf) # 克隆训练好的sgd_clf(随机梯度下降分类器)
# 划分训练集
X_train_flods = np.array(X_train)[train_index]
y_train_flods = y_train_5[train_index]
# 划分验证集
X_test_flods = np.array(X_train)[test_index]
y_test_flods = y_train_5[test_index]
clone_clf.fit(X_train_flods, y_train_flods) # 训练一折中的训练数据
y_pred = clone_clf.predict(X_test_flods) # 预测一折中的验证数据
n_correct = sum(y_pred == y_test_flods)
print(n_correct / len(y_pred))
运行结果：
交叉验证：
from sklearn.model_selection import cross_val_score # 交叉验证
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")
运行结果：
傻瓜版分类器
from sklearn.base import BaseEstimator
class Never5Classifier(BaseEstimator): # 傻瓜版的分类器
def fit(self, X, y=None):
return self # 这个训练其实就是没训练
def predict(self, X):
return np.zeros((len(X), 1), dtype=bool) # 这个预测是无论输入什么都归为0
never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train, y_train_5, cv=3, scoring="accuracy")
运行结果：
因为5的数据为占全部数据的1/10，所以随机的结果也很好，但是这种很好的表现是一种虚假的表现。
混淆矩阵
随机梯度下降分类器对应的混淆矩阵
计算混淆矩阵需要有预测值才能和实际目标比较，这里暂时不使用测试集，所以使用cross_val_predict替代
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
confusion_matrix(y_train_5, y_train_pred)
运行结果：
混淆矩阵最佳状态
y_train_perfect_predictions = y_train_5
confusion_matrix(y_train_5, y_train_perfect_predictions) # 一个完美分类器的混淆矩阵
运行结果：
精度和召回率
精度 = TP(真正类[判别为正类的真正的正类]) / (TP + FP(假正类[判断为正类的不是正类])) 判出来的真正的正类和真正的正类的比
召回率 = TP / (TP(真正类) + FN(假负类)) 判出来的真正的正类和所有被判为正类的比
from sklearn.metrics import precision_score, recall_score
precision_score(y_train_5, y_train_pred)
运行结果：
recall_score(y_train_5, y_train_pred)
运行结果：
从上面可以看出来，当一个数据是5时，有precision_score的概率是准确的， 只有recall_score的5被检测出来
将精度和召回率组合成单一的指标F1分数，F1分数是精度和召回率的谐波平均值，谐波平均值会给予低的值更高的权重，只有召回率和精度都很高时分类器才能得到较高的F1分数
F1 = 2 / (1/精度 + 1/召回率) = 2 * 精度 * 召回率 /（精度 + 召回率） = TP/（TP+（FN+FP）/2）
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)
运行结果：
F1对于精度和召回率相近的分类器有利
精度/召回率权衡
提高阈值精度提升，降低阈值会增加召回率降低精度
y_scores= sgd_clf.decision_function([some_digit])
y_scores
运行结果：
阈值为0的情况
threshold = 0
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred
运行结果：
阈值为8000的情况
threshold = 8000
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred
运行结果：
阈值对精度和召回率影响变化图像
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") # 返回决策函数
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
plt.plot(thresholds, precisions[:-1], "b--", label="Precison")
plt.plot(thresholds, recalls[:-1], "g-", label="Recall")
plt.xlim(-45000, 45000)
plt.ylim(0, 1)
plt.legend()
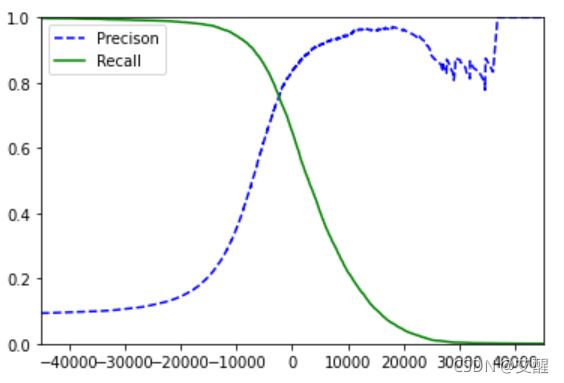
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.show()
确定阈值
假设现在要将精度设为90%，首先查阈值
np.argmax(precisions > 0.9) # 找到精度大于90%的阈值对应的索引
运行结果：
threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]
threshold_90_precision # 找到阈值
y_train_pred_90 = (y_scores >= threshold_90_precision)
precision_score(y_train_5, y_train_pred_90)
recall_score(y_train_5, y_train_pred_90)
plt.plot(recalls, precisions)
plt.show()
ROC曲线
受试者工作特征曲线（简称ROC）,描绘的是真正类率（召回率）和假正类率（FPR），FPR是被错误分为正类的负类实例的比值，等于1-真负类率（TNR）
from sklearn.metrics import roc_curve # 计算多种阈值的TPR和FPR
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
def plot_roc_curve(fpr, tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0, 1], [0, 1], 'k--')
plot_roc_curve(fpr, tpr)
plt.show()
这里面临一个折中权衡，召回率（TPR）越高，分类器产生的假正类（FPR）就越多，虚线表示纯随机分类器的ROC曲线，一个优秀的分类器应该离这个线越远越好
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores) # 有一种比较分类器的方法是测量曲线下面积（AUC）。完美的分类器的ROC AUC等于1，纯随机的ROC_AUC等于0.5
由于ROC曲线与精度/召回率（PR）曲线非常相似，当正类非常少见或者更关注假正类而不是假负类时，应该选择PR曲线，反之是ROC曲线
跟负类（非5）相比，正类（数字5）的数量真的很少，PR曲线清楚的说明分类器还有改进的空间
现在来训练一个随机森林分类器并比较他和随机梯度下降分类器的ROC曲线和ROC AUC分数
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3, method="predict_proba") # 因为随机森林没有decision_function,有的是predict_proba
roc_curve需要标签和分数，这里直接使用正类的概率作为分数值
y_probas_forest
y_score_forest = y_probas_forest[:, 1]
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5, y_score_forest)
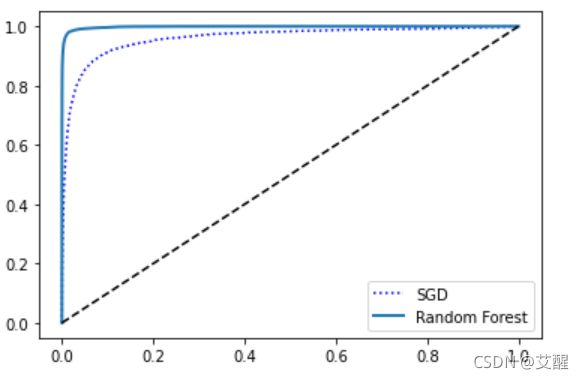
plt.plot(fpr, tpr,"b:", label="SGD")
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
plt.legend(loc="lower right")
plt.show()
比较ROC曲线，随机森林优于随机梯度下降
roc_auc_score(y_train_5, y_score_forest)
测试精度和召回率
precision_score(y_train_5, y_score_forest > 0.5) # 因为前面是标签类别，后面是概率，所以要按照概率形成标签
recall_score(y_train_5, y_score_forest > 0.5)
多类分类器
OvR与OvO
OvR策略：一对剩余 ；OvO策略：一对一
scikit-Learn 可以检测尝试使用二分类算法进行多类分类任务，会根据情况自动运行OvR,OvO, 下面用sklearn.svm.SVC类试试SVM分类器(SVM是支持向量机，这里就是拿来举个例子，后面的章节还会具体介绍)
from sklearn.svm import SVC
svm_clf = SVC()
svm_clf.fit(X_train, y_train) # 可以看到这里不是单纯的二分类了，而是10分类（0-9）
svm_clf.predict([some_digit])
在内部实际上训练了45个二元分类器，为了测试是否是这样，调用decision_function(),会返回10个分数
some_digit_scores = svm_clf.decision_function([some_digit])
some_digit_scores
from sklearn.multiclass import OneVsRestClassifier
ovr_clf = OneVsRestClassifier(SVC()) # 强制使用OvR
ovr_clf.fit(X_train, y_train)
ovr_clf.predict([some_digit])
随机梯度下降和随机森林
sgd_clf.fit(X_train, y_train)
sgd_clf.predict([some_digit])
sgd_clf.decision_function([some_digit])
cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring="accuracy")
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler() # 缩放
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64)) # 这里的fit_transform是将transform和fit结合在一起的，包含数据缩放和模型训练
cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring="accuracy")
误差分析
假设现在已经有了一个有潜力的模型，现在希望找到一些方法对其进一步改进，其中的一种方法就是分析其错误类型（误判的类型，即为什么会被误判）
y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
conf_mx = confusion_matrix(y_train, y_train_pred)
conf_mx
由于数字较多，并且不够直观，这里使用matshow(这个的作用是将矩阵绘制成图像，注意区分他和热力图的区别)查看混淆矩阵的图像表示
plt.matshow(conf_mx, cmap=plt.cm.gray)
plt.show()
大多数图片都在对角线上，说明基本上是被正确分类了（一个好的分类器的对角线是比较亮的）
row_sums = conf_mx.sum(axis=1, keepdims=True) # 按列求和（个人认为按行求和也可以）
norm_conf_mx = conf_mx / row_sums # 求占的比例
用0填充对角线，只保留错误，重新绘制结果（实际上就是降低亮度，来突出误判的亮度）
np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx, cmap=plt.cm.gray)
plt.show()
可以看到8的这个类别里面错误的分类要多，后续的优化可以针对8来进行（书中写的是搜集更多像8的数据，或者用算法计算闭环）
3和5误判的情况
def plot_digits(instances, images_per_row=10, **options): # 这里是参照网上的一个函数：https://github.com/ageron/handson-ml/issues/257
size = 28
images_per_row = min(len(instances), images_per_row)
images = [np.array(instances.iloc[i]).reshape(size, size) for i in range(instances.shape[0])] #change done here
if images_per_row == 0:
images_per_row = 0.1
n_rows = (len(instances) - 1) // images_per_row + 1
row_images = []
n_empty = n_rows * images_per_row - len(instances)
images.append(np.zeros((size, size * n_empty)))
for row in range(n_rows):
rimages = images[row * images_per_row : (row + 1) * images_per_row]
row_images.append(np.concatenate(rimages, axis=1))
image = np.concatenate(row_images, axis=0)
plt.imshow(image, cmap = plt.cm.binary, **options)
plt.axis("off")
cl_a, cl_b = 3, 5
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)] # 正确分为3的情况
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)] # 将3分为5的情况
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)] # 正确分为5的情况
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)] # 将5分为3的情况
plt.figure(figsize=(8, 8))
plt.subplot(221);plot_digits(X_aa[:25], images_per_row=5)
plt.subplot(222);plot_digits(X_ab[:25], images_per_row=5)
plt.subplot(223);plot_digits(X_bb[:25], images_per_row=5)
plt.subplot(224);plot_digits(X_ba[:25], images_per_row=5)
plt.show()
多标签分类
输出多个标签的分类器（之前介绍的分类器的结果都只有一个标签）
from sklearn.neighbors import KNeighborsClassifier # K临近算法
y_train_large = (y_train >= 7) # 将>=7的数称为大数
y_train_odd = (y_train % 2 == 1) # 奇数
y_multilabel = np.c_[y_train_large, y_train_odd] # 将两个标签合成多标签
print(y_multilabel.shape)
print(y_multilabel)
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_multilabel)
训练出来的模型预测结果包括两个标签，一个判断是不是大数，一个判断是不是奇数（这种方式不推荐，因为增加了模型的运算量，会影响精度，一般是先预测出数字，再判断是不是大数和奇数）
knn_clf.predict([some_digit])
y_train_knn_pred = cross_val_predict(knn_clf, X_train, y_multilabel, cv=3)
f1_score(y_multilabel, y_train_knn_pred, average="macro")
# 使用平均F1分数计算所有标签, 这里是假设不同标签具有同样的权值，若average=“weighted"则是给每个标签设置一个等于其自身支持的权值
多输出分类
大体上和多标签分类相似，是多标签分类的泛化，下面用图片降噪为例说明多输出分类
noise = np.random.randint(0, 100, (len(X_train), 784)) # 产生噪声(训练集)
X_train_mod = X_train + noise
noise = np.random.randint(0, 100, (len(X_test), 784)) # 产生噪声(测试集)
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test
some_index = 1 # 随便设置一个索引
plt.imshow(np.array(X_train_mod[some_index-1:some_index]).reshape((28, 28)), cmap="binary") # 噪声图片
plt.axis("off")
plt.show()
plt.imshow(np.array(y_train_mod[some_index-1:some_index]).reshape((28, 28)), cmap="binary") # 降噪图片
plt.axis("off")
plt.show()
knn_clf.fit(X_train_mod, y_train_mod)
clean_digit = knn_clf.predict(X_test_mod[some_index-1:some_index])
plt.imshow(np.array(X_test_mod[some_index-1:some_index]).reshape(28, 28), cmap="binary") # 降噪图片
plt.axis("off")
plt.show()
plt.imshow(np.array(clean_digit).reshape(28, 28), cmap="binary") # 降噪图片
plt.axis("off")
plt.show()
