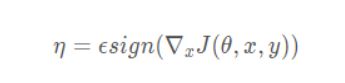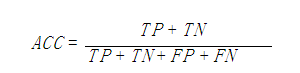FGSM和PGD算法的介绍与实际应用

基于FGSM/PGD算法的对抗样本的生成

在中文文本分类的场景下，以TextCNN（利用卷积神经网络对文本进行分类的算法）为基准模型，通过FGSM算法生成对抗样本进行训练，基于Pytorch实现。
对抗训练的核心步骤是：用被对抗性样本污染过的训练样本来训练模型，直到模型能学习到如此类型的抵抗。从而保证模型的安全性，在自动驾驶和图像识别领域，保证模型的安全性尤为重要。

中文数据集

从THUCNews中抽取了20万条新闻标题，文本长度在20到30之间。一共10个类别，每类2万条。 类别：财经、房产、股票、教育、科技、社会、时政、体育、游戏、娱乐。

运行环境

• Pytorch 1.6
• cuda 10.2
• cudnn 8.2
• python 3.6

实验参数

• batch_size 1024
• embedding_dim 128
• 训练集 18w
• 验证集 1w
• 测试集 1w

实验代码

FGSM

# FGSM
class FGSM:
    def __init__(self, model: nn.Module, eps=0.1):
        self.model = (
            model.module if hasattr(model, "module") else model
        )
        self.eps = eps
        self.backup = {}

    # 只攻击词embedding层
    def attack(self, emb_name='embedding'):
        for name, param in self.model.named_parameters():

            if param.requires_grad and emb_name in name:
                self.backup[name] = param.data.clone()
                r_at = self.eps * param.grad.sign()		#使用sign（符号）函数，将对x求了偏导的梯度进行符号化
                param.data.add_(r_at)

    def restore(self, emb_name='embedding'):
        for name, para in self.model.named_parameters():
            if para.requires_grad and emb_name in name:
                assert name in self.backup
                para.data = self.backup[name]

        self.backup = {}

---

PGD

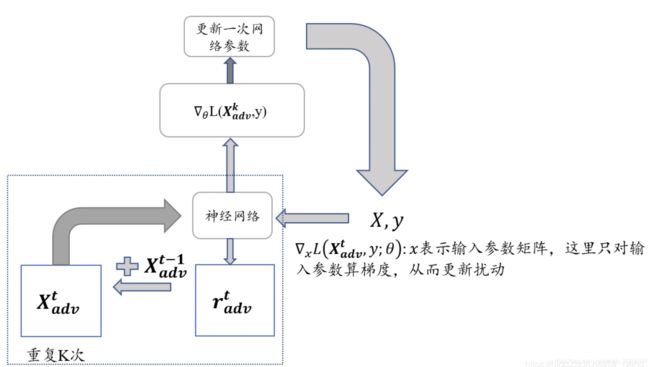
相比较于FGM的一步对抗到位，PGD采用小步多走的策略进行对抗。具体来说，就是一次次地进行前后向传播，一次次地根据grad计算扰动r，一次次地将新的扰动r累加到embedding层的grad上，若超出一个范围，则再映射回给定范围内。最终，将最后一步计算得到的grad累加到原始梯度上。即以累加过t步扰动的梯度对应的grad对原梯度进行更新。

由上面公式（1）（2）可以看出，在一步更新网络内（公式2），在S 范围内进行了多步小的对抗训练（公式1）,在这多步小的对抗训练中，对wordEmbedding空间扰动是累加的。每次都是在上一次加扰动的基础上再加扰动，然后取最后一次的梯度来更新网络参数。

---

前置：设置PGD的扰动积累步数为K步
计算在正常embedding下的loss和grad（即先后进行forward、backward），在此时，将模型所有grad进行备份；
K步的for循环: # 反向传播(计算grad)是为了计算当前embedding权重下的扰动r。同时为了不干扰后序扰动r的计算，还要将每次算出的grad清零
a. 对抗攻击：如果是首步，先保存一下未经attack的grad。然后按照PGD公式以及当前embedding层的grad计算扰动，然后将扰动累加到embedding权重上；
b. if-else分支：
i. 非第K-1步时：模型当前梯度清零；
ii. 到了第K-1步时：恢复到step-1时备份的梯度（因为梯度在数次backward中已被修改）；
c. 使用目前的模型参数（包括被attack后的embedding权重）以及batch_input，做前后向传播，得到loss、更新grad
恢复embedding层2.a时保存的embedding的权重（注意恢复的是权重，而非梯度）
optimizer.step()，梯度下降更新模型参数。这里使用的就是累加了K次扰动后计算所得的grad

# PGD
class PGD:
    def __init__(self, model, eps=0.1, alpha=0.3):
        self.model = (
            model.module if hasattr(model, "module") else model
        )
        self.eps = eps
        self.alpha = alpha
        self.emb_backup = {}
        self.grad_backup = {}

    def attack(self, emb_name='embedding', is_first_attack=False):
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name:
                if is_first_attack:
                    self.emb_backup[name] = param.data.clone()
                norm = torch.norm(param.grad)
                if norm != 0 and not torch.isnan(norm):
                    r_at = self.alpha * param.grad / norm
                    param.data.add_(r_at)
                    param.data = self.project(name, param.data)

    def restore(self, emb_name='embedding'):
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name:
                assert name in self.emb_backup
                param.data = self.emb_backup[name]
        self.emb_backup = {}

    def project(self, param_name, param_data):
        r = param_data - self.emb_backup[param_name]
        if torch.norm(r) > self.eps:
            r = self.eps * r / torch.norm(r)
        return self.emb_backup[param_name] + r

    def backup_grad(self):
        for name, param in self.model.named_parameters():
            if param.requires_grad and param.grad is not None:
                self.grad_backup[name] = param.grad.clone()

    def restore_grad(self):
        for name, param in self.model.named_parameters():
            if param.requires_grad and param.grad is not None:
                param.grad = self.grad_backup[name]

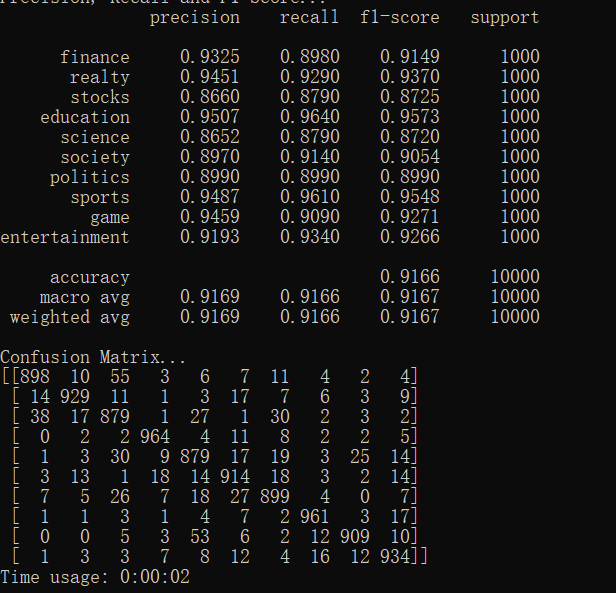
如下展示FGSM算法运行结果

结果

补充

【Confusion Matrix】混淆矩阵，我们希望的是绿色的部分的数值尽可能地大，橙色部分的数值尽可能地小。这样模型的效果是更好的。

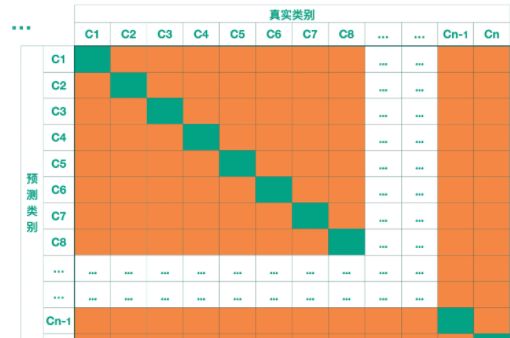
混淆矩阵

• True Positive(真正，TP)：将正类预测为正类数

• True Negative(真负，TN)：将负类预测为负类数

• False Positive(假正，FP)：将负类预测为正类数误报 (Type I error)

• False Negative(假负，FN)：将正类预测为负类数→漏报 (Type II error)
  

【Accuracy】准确度，计算公式

【sensitive】灵敏度，sensitive = TP/P，表示的是所有正例中被分对的比例，衡量了分类器对正例的识别能力。

【recall】召回率是覆盖面的度量，度量有多个正例被分为正例recall=TP/(TP+FN)=TP/P=sensitive，可以看到召回率与灵敏度是一样的。

以上三个指标均是衡量机器学习的评价标准。

代码

链接：https://pan.baidu.com/s/1Jw9DIi7WM_IynI6LITmBjw
提取码：romy

【参考】

对抗学习总结：FGSM-＞FGM-＞PGD-＞FreeAT, YOPO -＞FreeLb-＞SMART-＞LookAhead-＞VAT