技术干货 | 基于MindSpore的图算融合探索和实践

还记得一年前的MindSpore 0.5版本中，我们怀着忐忑的心情首次发布了图算融合特性，主要支持了昇腾硬件平台。在该版本中，图算融合初步实现了图算一体的DSL表达能力，并打开了图算协同优化的大门。

在之后的一年里面，我们持续进行了大量的特性完善和开发增强。随着MindSpore 1.3版本的发布，图算融合刚好满一岁！我们也正好借这个契机跟大家聊一聊图算融合这一年来收获的经验和教训。

01

为什么需要图算融合？

1.1 计算图和算子再认识

包括MindSpore在内的AI框架，不约而同都采用计算图实现网络结构的表达。所以也间接证明了计算图在AI框架中强大的生命力。那么到底什么是计算图呢？

我们引用[tutorialspoint]中的一段话来介绍：

A computational graph is defined as a directed graph where the nodes correspond to mathematical operations. Computational graphs are a way of expressing and evaluating a mathematical expression.

For example, here is a simple mathematical equation .

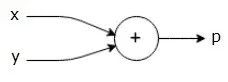
 P = x + y

We can draw a computational graph of the above equation as follows.

总结来说，计算图是一个以算子（Operators）为节点的有向图所表达的计算函数。在AI框架里面，这个计算函数对输入tensor依次调用执行有向图中的算子节点，并得到最终的输出tensor。

那么什么是算子呢？引用Wikipedia：

In mathematics, an operation is a function which takes zero or more input values (called operands) to a well-defined output value. The number of operands is the arity of the operation.

所以，算子本质还是一个计算函数。在AI框架里面，这个计算函数还是对输入tensor依次进行若干内部处理，然后得到最终的输出tensor。那么算子的内部处理都是什么呢？通过对大量的算子进行分析，我们会发现，绝大部分算子都是可以拆分为若干更为基本的算子组成的的子图，比如Sigmoid，其内部计算可以用如下计算图表示：

通过以上分析，我们不难发现，计算图和算子在计算本质上是一致的。算子是打包后的计算图，计算图是拆包后的算子。所以理论上，我们可以定义一个小规模的“基本算子”集合，然后通过一个或多个基本算子组合去等价表达任何的现有算子。从而进一步表达任意的现有计算图。

既然用小规模的“基本算子”集合就可以表达任意现有计算图。为什么现有主流AI框架还要定义大量的、本来可以用基本算子等价实现的复合算子呢？这个问题背后的主要原因还是性能。相比多个基本算子组成的计算图，使用复合算子可以具有更好的计算和内存局部性，从而获得更好的执行性能。这是不难理解的，因为对于基本算子计算图来说，相邻算子之间只能通过全局内存（或显存）进行数据传递。而对于复合算子来说，相邻的基本计算之间则可以通过局部内存或者寄存器进行数据传递。除了性能之外，在一些场景下，通过算子融合也能有效减少对全局内存的的实际占用。

1.2 为什么需要图算融合

基于以上分析可见，相比复合算子，基本算子具有更好的通用组合表达能力，同时使得AI框架在算子支持方面更为精简。但相比基本算子，复合算子在性能方面存在优势。可以简单图示如下：

对于以上问题，我们是否可以通过某些技术同时兼顾？或者更具体地，使得上图的“计算性能”线变为水平？

另一方面，我们在通过AI框架提供的算子表达计算网络时，通常是混合使用不同复合程度的算子。比如LayerNorm由12个基本算子组成，而Relu则只有1个基本算子。所以，对于这种不同复合程度的算子组成的计算图，从整体执行性能角度，我们是否可以将他们组合成更为合理的复合粒度算子，来获得最佳的整体计算图性能？

在TVM、XLA等自动算子编译技术出现之前，AI框架主流采用手工融合的方式解决如上问题。主要思路是：

1）识别常见的热点算子组合子图，比如：Add(Mul(x, y))。然后针对该算子子图手工实现对应融合算子；

 2）将融合算子注册到AI框架，并在AI框架中增加对应的优化pass，将匹配的算子子图替换为融合算子节点。

这种方式的缺点是显而易见的。因为它只能针对若干热点场景进行融合，所以是无法做到通用和泛化的。

基于以上问题背景，并结合MindSpore自身需求，我们提出图算融合解决方案。其主要思路是：

1）以通用的pattern识别计算图中的融合场景，并生成融合算子子图；

2）将生成的融合算子子图通过自动算子编译技术（AKG）生成对应的融合算子。

通过图算融合之后，用户在进行网络定义时，不管使用组合表达能力更强的基本算子，还是复合算子。最终都将通过图算融合重新组织和融合，并替换为最优复合粒度的融合算子。

02

业界相关技术

2.1 XLA

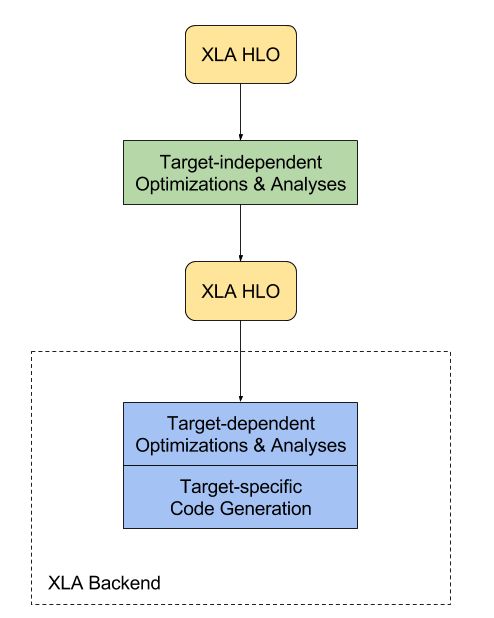
XLA最早基于TensorFlow开发。不过它采用了与TensorFlow不同的计算图IR表示。所以在TensorFlow中，需要将TensorFlow的计算图IR首先转换为XLA的计算图IR（HLO）。然后XLA基于HLO进行融合优化等，最后通过LLVM等后端编译生成相应融合算子。

由于采用独立的IR，XLA具有较好的可移植性，目前在PyTorch、JAX等非TensorFlow框架中也有不错的表现。

图片来源：https://www.tensorflow.org/xla/architecture

2.2 TVM

TVM主要用于推理场景。在架构上，主要包括relay和tir两层。其通过relay导入推理模型，然后进行融合优化，最后通过tir生成融合算子。

TVM在算子编译方面采用compute和schedule分离的技术，并且不同算子compute所需要的schedule通常是不同的。为了更好支持不同融合算子场景，TVM支持对算子进行自动tuning，来生成较优的切分参数甚至schedule。由于tuning空间较大，目前tuning时间相对还是比较长的。根据笔者曾经使用经验，平均每个算子应该在20~30分钟以上。

图片来源：https://tvm.apache.org/docs/dev/index.html#example-compilation-flow

03

图算融合设计思考

3.1 MindIR原生设计

在MindSpore内部，是使用MindIR来表示计算图。MindIR除了支持普通计算图表达，还可以支持子图表达。每个子图等价于一个子计算函数，并且可以被其它计算图调用。

为了方便处理，图算融合直接基于MindIR子图来表达图算融合不同处理阶段的计算逻辑，比如：

1）为了避免对已有网络的直接修改，并实现优化，我们会自动将复合算子展开成复合算子图；

2）将相邻的复合算子子图聚合成更大的聚合算子子图；

3）根据融合策略，将聚合算子子图拆分拆分为多个融合算子子图。每个融合算子子图最终通过akg编译生成可执行融合算子。

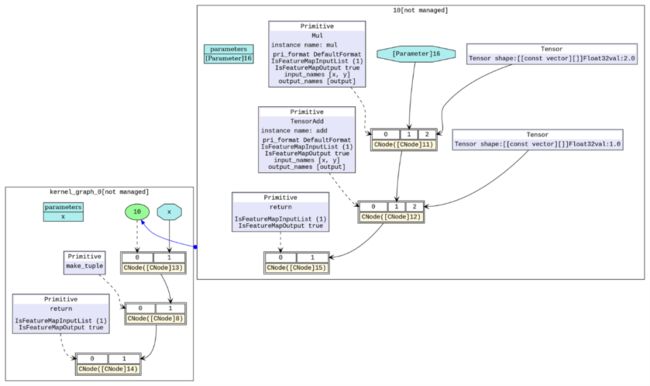
MindIR子图如下所示：

大家可能会疑惑：XLA采用独立的IR有那么多好处，为什么我们反其道而行之，采用MindIR原生设计呢？

所有的设计决策都是在做取舍。所以这个问题本质是由设计目的决定的。由于我们没有MindSpore之外单独使用的需求，所以我们可以抛开这个包袱，直接基于MindIR原生表达，并获得如下好处：

1）可以直接复用MindSpore的已有公共优化和基础设施，大大减少代码开发量；

2）可以实现于MindSpore统一的运行时内存分配管理、流分配等；

3）图层知道算子内的计算逻辑，进行更多全局优化（比如跨子图等）。

3.2 Polyhedral调度技术

在AKG算子编译层面，我们通过polyhedral技术进行自动的算子优化和生成。借助于Polyhedral编译技术，能够对算子的迭代空间进行依赖分析，自动生成兼顾并行性与数据局部性的调度。同时，迭代空间的依赖关系还能帮助我们完成循环重排、循环融合、循环切分等变换优化，进而达到较优的执行性能。

相比业界其它自动算子生成能力，我们采用Polyhedral技术主要好处：

1）不需要手工指定schedule，以及schedule空间的tuning。从而支持任意的融合算子编译生成。使得图算融合应用于JIT训练场景成为可能；

2）能够有效提升算子融合深度及融合算子泛化能力。在针对单算子或一个独立的循环嵌套进行优化时，Polyhedral模型并不能轻易地得到与手工优化算子库或其它通过手工指定调度的方法相当的性能，但是在多个算子融合或多个循环嵌套之间快速寻找优化手段方面，Polyhedral却有着相对较大的优势。我们在ModelZoo上的泛化验证结果也证明，无论是在融合算子的规模（200+融合算子），还是融合pattern的复杂程度（多输出、多算子类型）上，AKG都能够快速高效的生成对应的kernel。

3.3 图算协同优化

由于图算融合同时介入图层（MindSpore）以及算子层（AKG）。所以相比业界实现，我们可以非常方便实现一些图层和算子层协同优化的技术。

· 3.3.1通过原子加实现Reduction融合类算子性能提升

在很多网络中，ReduceSum具有非常广泛的应用。由于ReduceSum的数据累加天然不具备数据并行性，目前业界通常的算子实现是单block（核）的算子，多核资源利用率较低。

为了解决该问题，我们与AKG协同，通过使用原子加指令，使得ReduceSum可以实现多block进行。其算子原理是：将累加计算分摊到不同的并行block上，每个block首先完成block内的累加，然后通过原子加方式向外部global内存做输出结果累加。

在实现上，我们重点解决了两个问题：

1）ReduceSum的输出Tensor内存必须依赖算子外部进行清零，我们在图层预先识别需要使能原子加的融合算子，并提前插入初始化清零算子；

2）通过poly schedule生成高性能的原子加融合算子。利用poly多面体模型和自动切分求解实现调度变换，并调用高性能的模板类库实现Block内的reduce计算，如下图所示：

实验数据表明，在大shape场景下，akg的reduction算子性能提升显著，如表1所示（数据类型为float32）。

表1 不同场景下AKG与cudnn、TVM 、Ansor测试reduce_sum算子性能对比（单位：us）

· 3.3.2将部分Gemm类算子替换为AKG实现

对于一些特定类型的Gemm算子，cuBLAS等第三方库尚未达到性能最优。对于这类算子，我们将其替换为对应的AKG实现，从而实现了更好的性能收益。

Gemm算子编译优化全流程如上图所示。在AKG的Polyhedral调度优化中，针对Gemm算子依次进行了自适应切分参数生成、多层级切分、Warp级循环轴映射、多层级内存提升以及GPU资源重映射等。同时，在后端优化流程，也针对GEMM实现/使能了部分通用优化pass，包括对共享内存重排以避免Bank冲突、分析处理矩阵生命周期以提高内存利用率、向量化数据加载以增大吞吐、数据预取以形成计算-存取流水等。

我们对Gemm类算子性能进行了实验测试，部分测试结果如表所示。泛化验证中发现，对于规约轴小于某阈值的场景，AKG性能优于cuBLAS，达到了110~300%；因此，当前1.3版本中，通过规则部分打开了混合精度网络模型中的Gemm类算子，在不同神经网络模型的不同BatchSize下，与原方案（cuBLAS）相比，整网收益2~8%不等。

表2 不同场景下AKG与cuBLAS/cuDNN、TVM测试Gemm类算子性能对比

此外，我们还基于polyhedral调度实现了Gemm与Elemwise算子的融合能力。通过扩展API以及对融合矩阵的调度优化，在Fragment级别实现了Gemm与Elemwise计算融合，从而达到更优的性能。下表示例为Gemm + BiasAdd的融合，同cuBLAS/cuDNN相比，整体性能提升可达50%-70%。

表3 不用场景下AKG与cuBLAS/cuDNN测试Gemm+BiasAdd融合性能对比

04

性能评测

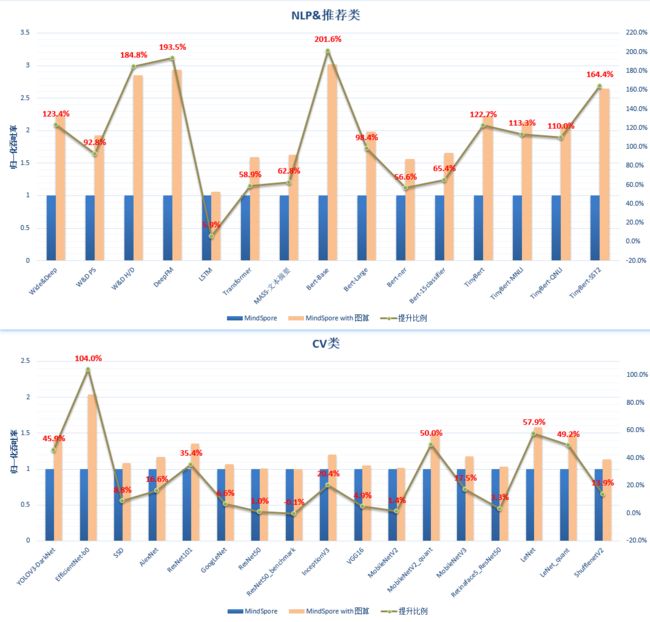
在MindSpore 1.3版本中，我们对GPU的支持做了极大的完善和增强。通过对Model Zoo大量GPU网络进行验证，图算融合平均性能提升：NLP类96.4%↑；推荐类136.6%↑; CV类30.7%↑。

05

参考资料

[1] XLA. https://www.tensorflow.org/xla

[2] TVM. https://tvm.apache.org/

[3] MindSpore. https://www.mindspore.cn/

[4] AKG. https://gitee.com/mindspore/akg  

[5] Jie Zhao, Bojie Li等. 2021. AKG: Automatic Kernel Generation for Neural Processing Units using Polyhedral Transformations. (PLDI 2021). https://doi.org/10.1145/3453483.3454106

[6] Jie Zhao,Peng Di. 2020. Optimizing the Memory Hierarchy by Compositing Automatic Transformations on Computations and Data. (MICRO-53). https://doi.org/10.1109/MICRO50266.2020.00044

[7] Polyhedral编译调度算法(1)——Pluto算法, 赵捷. https://zhuanlan.zhihu.com/p/199683290