车间调度建模系列4|扩展析取图之工序相关性
获取更多资讯,赶快关注公众号(名称:智能制造与智能调度,公众号:deeprlscheduler)吧!
三维析取图模型建模系列目录
- 复杂车间调度问题三维析取图建模系列预告
- 车间调度建模系列1|复杂车间调度问题特点
- 车间调度建模系列2|复杂车间调度问题描述
- 车间调度建模系列3|复杂车间调度问题解的表示
- 车间调度建模系列4|扩展析取图之工序相关性)(本文)
完整的符号说明详见车间调度建模系列2|复杂车间调度问题描述。
经典的二维析取图模型仅表达了工艺路线决定的顺序约束,无法表达时间约束(如最早开始、最晚结束)、资源约束(如机床偏好和调整)、流转方式(如平顺)、交互约束(如锁定)等其他类型的约束,因此在传统模型的基础上对其进行扩展得到了赋时三维析取图模型,并使用集合 G = ( N , N ′ , C , E , F ) G=\left(N, N^{\prime}, C, E, F\right) G=(N,N′,C,E,F)来表达,其中 N N N表示所有实节点 O i h m O_{ihm} Oihm集合, N ′ N^{\prime} N′为所有虚节点 O i ′ h ′ m ′ O_{i^{\prime} h^{\prime} m^{\prime}} Oi′h′m′的集合, O i ′ h ′ m ′ O_{i^{\prime} h^{\prime} m^{\prime}} Oi′h′m′表示工件 i ′ i^{\prime} i′的第 h ′ h^{\prime} h′道工序不存在或不能在机床上 m ′ m^{\prime} m′加工; C C C为有向实线(连接弧)集合,表示同一零件下各工序的工艺顺序; E E E为无向虚线(析取弧)集合,连接可在同一机床上加工的两道工序; F F F为双点划线(可选弧)集合,表示只能从连接的节点中选择一个,即同一零件的同一工序只能在一台机床上加工。新的模型通过增加虚节点集合 N ′ N^{\prime} N′和可选弧集合 F F F来表达工序的多台可选机床约束,此外,还增加了工序相关性约束以丰富连接弧集合 C C C,并通过考虑工序间物流周转时间、顺序不依赖准备时间、机床选择偏好和资源日历得到弧权重的五元组表达。
工序相关性
工序相关性定义
经典的析取图模型仅仅表达了工艺路线决定的顺序约束,却无法表达在许多复杂制造企业中广泛存在的另外2类约束。一类为延迟约束,即工件的前一道工序加工完成后,需要延迟一定时间其当道才能开始加工。例如,当某一热处理工序完成后,其下一道工序需要先进行一段时间的冷却处理后才能开始加工;另一类为工件之间的工艺约束。这类约束在工件之间存在装配关系时最为常见,在人机交互调度中,当调度员设置工序不允许影响时,也会建立这种约束关系。这两类工艺约束在实际调度中是存在且不能忽略的,为此给出工序相关性定义如下:
定义1:工序相关性。除常规的工艺路线顺序约束外,不同工序的开始时间及完成时间之间存在的某种顺序约束及延时约束,称为工序相关性。
定义2:相关前工序和相关后工序。若两道工序之间存在工序相关性,则称前面的工序为相关前置工序,后面的工序为相关后置工序。
工序相关性可分为4种类型:开始—开始相关、开始—结束相关、结束—开始相关和结束—结束相关。具体意义为:若两道工序存在“开始—开始”相关,则表示相关前工序开始加工一定时间后,相关后工序才能开始加工;若存在“结束—开始”相关,则表示相关前工序结束加工一定时间后,相关后工序才能开始加工,其余类型的意义类推。
工序相关性数学描述
若某两道工序 O i h O_{ih} Oih, O j l ( h ≠ l ) O_{jl}(h \neq l) Ojl(h=l)之间存在相关性,则用一个二元组 R j l i h = ( t j l i h , g j l i h ) R_{j l}^{i h}=\left(t_{j l}^{i h}, g_{j l}^{i h}\right) Rjlih=(tjlih,gjlih)表示,其中 t j l i h t_{j l}^{i h} tjlih为相关性类型, g j l i h g_{j l}^{i h} gjlih为相关时间。
开始—开始、开始—结束、结束—开始和结束—结束4种相关性类型分别表示为SS,SF,FS和FF。将所有类型表示为一个集合,记为: T = { S S , S F , F S , F F } T=\{S S, S F, F S, F F\} T={SS,SF,FS,FF}。因此有: t j l i h ∈ T t_{j l}^{i h} \in T tjlih∈T。此外,不失一般性,令相关时间 g j l i h ≥ 0 g_{j l}^{i h} \ge 0 gjlih≥0。
对 R j l i h = ( S S , g j l i h ) R_{j l}^{i h}=\left(S S, g_{j l}^{i h}\right) Rjlih=(SS,gjlih),有
S i h m ≥ S j l n + g j l i h (2.7) S_{i h m} \geq S_{j l n}+g_{j l}^{i h}\tag{2.7} Sihm≥Sjln+gjlih(2.7)
对 R j l i h = ( S F , g j l i h ) R_{j l}^{i h}=\left(S F, g_{j l}^{i h}\right) Rjlih=(SF,gjlih),有
C i h m ≥ S j l n + g j l i h (2.8) C_{i h m} \geq S_{j l n}+g_{j l}^{i h}\tag{2.8} Cihm≥Sjln+gjlih(2.8)
对 R j l i h = ( F S , g j l i h ) R_{j l}^{i h}=\left(F S, g_{j l}^{i h}\right) Rjlih=(FS,gjlih),有
S i l m ≥ C j l n + g j l i h (2.9) S_{i l m} \geq C_{j l n}+g_{j l}^{i h}\tag{2.9} Silm≥Cjln+gjlih(2.9)
对 R j l i h = ( F F , g j l i h ) R_{j l}^{i h}=\left(F F, g_{j l}^{i h}\right) Rjlih=(FF,gjlih),有
C i l n ≥ C j l n + g j l i h (2.10) C_{i l n} \geq C_{j l n}+g_{j l}^{i h}\tag{2.10} Ciln≥Cjln+gjlih(2.10)
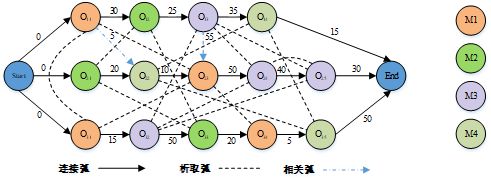
如图8所示,在工艺路线顺序约束中,相邻两道工序之间的连接弧上的权重表示的是前道工序的加工时间,其可以理解为前道工序开始一定时间(该工序加工时间)后后道工序才能开始,所以按照工序相关性的定义,在工艺路线顺序约束中相邻两道工序的关系类似于工序相关性 R j l i h = ( S S , g j l i h ) R_{j l}^{i h}=\left(S S, g_{j l}^{i h}\right) Rjlih=(SS,gjlih),因此为在析取图中能够全面表达不同相关性类型的同时又能简化模型,需要将其他三种类型转换成“开始—开始”,其转换推导如下:
对于“开始—结束”相关性 ,由式(2.8)可得
C i l m ≥ S j l n + g j l i h ⇒ S i l m + P i h m ≥ S j l n + g j l i h ⇒ S i l m ≥ S j l n + ( g j l i h − P i l m ) (2.11) C_{i l m} \geq S_{j l n}+g_{j l}^{i h} \Rightarrow S_{i l m}+P_{i h m} \geq S_{j l n}+g_{j l}^{i h} \Rightarrow S_{i l m} \geq S_{j l n}+\left(g_{j l}^{i h}-P_{i l m}\right)\tag{2.11} Cilm≥Sjln+gjlih⇒Silm+Pihm≥Sjln+gjlih⇒Silm≥Sjln+(gjlih−Pilm)(2.11)
因此“开始—结束”相关性向“开始—开始”的转换可表示为:
R j l i h = ( S F , g j l i h ) ⇔ R j l i h = ( S S , g j l i h − P i h m ) (2.12) R_{j l}^{i h}=\left(S F, g_{j l}^{i h}\right) \Leftrightarrow R_{j l}^{i h}=\left(S S, g_{j l}^{i h}-P_{i h m}\right)\tag{2.12} Rjlih=(SF,gjlih)⇔Rjlih=(SS,gjlih−Pihm)(2.12)
同理,可得其他两种类型的相关性向“开始—开始”类型转换的等价式为:
R j l i h = ( F S , g j l i h ) ⇔ R j l i h = ( S S , g j l i h + P j l n ) (2.13) R_{j l}^{i h}=\left(F S, g_{j l}^{i h}\right) \Leftrightarrow R_{j l}^{i h}=\left(S S, g_{j l}^{i h}+P_{j l n}\right)\tag{2.13} Rjlih=(FS,gjlih)⇔Rjlih=(SS,gjlih+Pjln)(2.13)
R j l i h = ( F F , g j l i h ) ⇔ R j l i h = ( S S , g j l i h + P j l n − P i h m ) (2.14) R_{j l}^{i h}=\left(F F, g_{j l}^{i h}\right) \Leftrightarrow R_{j l}^{i h}=\left(S S, g_{j l}^{i h}+P_{j l n}-P_{i h m}\right)\tag{2.14} Rjlih=(FF,gjlih)⇔Rjlih=(SS,gjlih+Pjln−Pihm)(2.14)
工序相关性约束
除了工艺顺序和机床能力约束外,由于引入了工序相关性约束,工序的最早开始时间和最早结束时间将受制于相关前置工序。设 P r e d O R i h PredOR_{ih} PredORih为工件 i i i的第 h h h道工序的相关前置工序集合,则
当相关性类型为“开始—开始”即 t j l i h = S S t_{j l}^{i h}=S S tjlih=SS时,最早开始时间 E S i h m = max { C i ( h − 1 ) r , C i ′ h ′ m , max { S j l n + g j l i h } } E S_{i h m}=\max \left\{C_{i(h-1) r}, C_{i^{\prime} h^{\prime} m}, \max \left\{S_{j l n}+g_{j l}^{i h}\right\}\right\} ESihm=max{Ci(h−1)r,Ci′h′m,max{Sjln+gjlih}},其中工序 O j l ∈ Pred O R i h O_{j l} \in \operatorname{Pred} O R_{i h} Ojl∈PredORih;
当相关性类型为“结束—开始”即 t j l i h = F S t_{j l}^{i h}=F S tjlih=FS时,最早开始时间 E S i h m = max { C i ( h − 1 ) r , C i ′ h ′ m , max { C j l n + g j l i h } } E S_{i h m}=\max \left\{C_{i(h-1) r}, C_{i^{\prime} h^{\prime} m}, \max \left\{C_{j l n}+g_{j l}^{i h}\right\}\right\} ESihm=max{Ci(h−1)r,Ci′h′m,max{Cjln+gjlih}},其中工序 O j l ∈ Pred O R i h O_{j l} \in \operatorname{Pred} O R_{i h} Ojl∈PredORih;
当相关性类型为“开始—结束”即 t j l i h = S F t_{j l}^{i h}=S F tjlih=SF时,最早结束时间 E C i h m = max { S i h m + P i h m , max { S j l n + g j l i h } } E C_{i h m}=\max \left\{S_{i h m}+P_{i h m}, \max \left\{S_{j l n}+g_{j l}^{i h}\right\}\right\} ECihm=max{Sihm+Pihm,max{Sjln+gjlih}},其中工序 O j l ∈ Pred O R i h O_{j l} \in \operatorname{Pred} O R_{i h} Ojl∈PredORih;
当相关性类型为“结束—结束”即 t j l i h = F F t_{j l}^{i h}=F F tjlih=FF时,最早结束时间 E C i h m = max { S i h m + P i h m , max { C j l n + g j l i h } } E C_{i h m}=\max \left\{S_{i h m}+P_{i h m}, \max \left\{C_{j l n}+g_{j l}^{i h}\right\}\right\} ECihm=max{Sihm+Pihm,max{Cjln+gjlih}},其中工序 O j l ∈ Pred O R i h O_{j l} \in \operatorname{Pred} O R_{i h} Ojl∈PredORih。
在经典析取图中增加虚线箭头表示相关弧,如下图所示。