推荐系统—基于物品的协同过滤（一）

推荐系统—基于物品的协同过滤（一）

前言

​ ​ 最近在工作当中接到一个关于推荐系统相关的需求，于是对推荐系统这一块进行了学习和调研，于是想对推荐系统做一些记录和总结。

什么是推荐系统

​ ​ 随着移动互联网的发展，我们进入了信息爆炸的时代，面对海量的信息使得用户的选择变得困难，同时用户的需求也变得不那么明确。如何在用户需求不明确的情况下，从海量的历史数据中寻找用户感兴趣的信息，成为了推荐系统需要解决的主要问题。推荐系统的本质是在用户需求不明确的情况下，通过机器学习、深度学习技术结合用户历史数据构建兴趣模型，为用户提供精准的个性化推荐帮助用户减少用户搜索成本，提高资源配置效率。推荐系统也被称为互联网的“增长引擎”。

出现的原因

​ ​ 信息过载；
​ ​ 个性化表达的需要；
​ ​ 特定场景下，个人对自己的需求不是那么明显。

作用意义

​ ​ 用户角度（用户体验优化）：推荐系统解决用户在“信息过载”的情况下，用户如何高效获得感兴趣信息的问题。
 ​ 公司角度（公司商业利益）：最大限度地吸引用户、留存用户、增加用户黏性、提高用户转化率，从而达到商业目标连续增长、增加公司收益（新闻类：点击率，电商类：购买转换率，视频类：观看时长等）。

发展历程

​ ​ 协同过滤、逻辑回归<2010年之前> =》因子分解、梯度提升树、组合模型 =》深度学习推荐模型<2015年之后>。

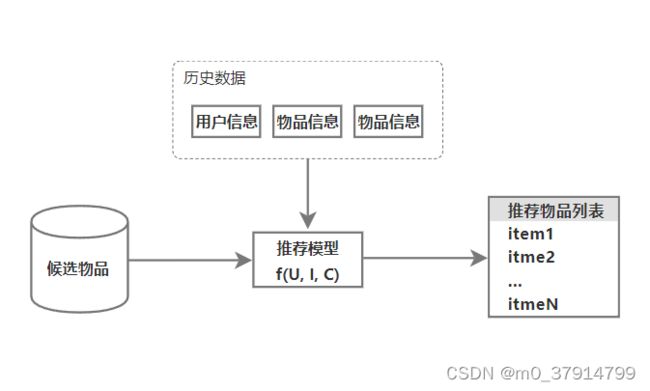
逻辑框架

​ ​ 在已经获取的“用户信息”、“物品信息”，“场景信息”数据基础上，对于用户U(user)在一个特定场景C(context)下，针对海量的物品信息，构建一个函数f(U, I, C)，用这个函数f预测用户对特定候选物品I（items）的喜好程度，然后对喜好程度进行排序，选取喜好程度最大的Top(n)个候选物品作为推荐列表展示给用户。

相关算法

 ​  协同过滤(Collaborative Filtering) 是一种在推荐系统广泛使用的技术，2003年由Amazon发表的论文中提出，并迅速成为业界主流的推荐模型，尽管今天已经在推荐系统中引入了深度学习，但模型的基本原理还是没有脱离经典协同过滤的思路。该技术主要通过分析用户或者事务之间的相似性，来预测用户可能感兴趣的内容并将此内容推荐给用户。这里的相似可以是人口特征的相似，也可以是历史浏览人内容的相似，还可以是一个人通过一定机制给与某个事务的回应。假如有两个人A和B是很好的朋友，并且都是人工智能方面的研发者，他们都喜欢看书，那么协同过滤会认为他们两个的相似度很高，会将A喜欢看的书而B没有看的书推荐给B。
 ​ 协同过滤的算法分以下几种：
 ​  ​ a.基于内容的协同过滤（ItemCF思想精髓物以类聚）；
 ​  ​ b.基于用户的协同过滤（UserCF思想精髓人以群分）；
 ​  ​ c.矩阵分解模型LFM（Latent Factor Model，加入了隐向量的概念）。
 ​ 逻辑回归（Logistic Regression, LR） 协同过滤只是应用用户和物品之间的显示信息或者隐式信息，LR可以利用和融合更多用户、物品的上下文特征。LR模型是一种宽而不深的结构，模型优点是简单、可控性好，但是效果的好坏直接依赖特征工程的程度，需要非常精细的连续型、离散型、实践型等特征。
 ​ 逻辑回归的算法有以下几种：
 ​  ​ a.逻辑回归（Logistic Regression，LR）
 ​  ​ b.大规模分片线性模型（Large Scale Piece-wise Linear Model, LS-PLM）
 ​ 因子分解机模型（Factorization Machines, FM） 考虑了特征间的交叉，对所有嵌套变量交互进行建模，因此相比LR模型FM在数据非常稀疏的情况下，依然可以估计出可靠参数进行预测。此外FM也可以用线性时间来计算，同时还能够与许多优秀的协同过滤方法相融合。FM在推荐系统和广告领域关注的点击率（Click-through Rate，CTR）和转化率（Conversion Rate，CVR）两项指标上有着良好的表现。
 ​ FM模型算法有以下两种：
 ​  ​ a.因子分解机（Factorization Machines, FM）
 ​  ​ b.域感知因子分解机（Field-aware Factorization Machine，FFM）通过加入域的概念，进一步加强了FM的特征交叉的能力
 ​ 组合模型 为了融合多个模型的优点，将不同的模型组合使用。像Facebook提出的梯度提升决策树（Gradient Boosting Decision Tree，GBDT）+ 逻辑回归模型（Logical Logistic Regression）是目前业界影响力最大的组合方式，还有结合深度学习算法的DeepFM和处于探索阶段的NFM将FM进行神经网络化尝试等等。

协同过滤

 ​ 协同大家的反馈、评价和意见，一起对海量信息进行过滤，从中筛选出目标用户可能感兴趣的信息的推荐过程。通过研究搜集具有类似偏好或属性的用户数据来主动向用户推荐最需要的资源。通用做法是收集和维护关于用户喜好的数据，然后通过算法从数据中分析出具有相似口味的用户，最后根据要推荐用户的相似用户的喜好向其推荐商品即可。

基于物品的协同过滤算法

 ​ 本文主要是介绍基于物品的协同过滤算法的原理及代码实现。ItemCF是目前业界使用最广泛，同时也是最容易落地的算法之一，像亚马逊、YouTube他们的推荐算法基础都是基于ItemCF的。假设你是一个户外运动爱好者，你在某个App上面买了一个登山杖，然后App给你推荐了一双登山鞋，实现这样一套逻辑的背后就是ItemCF在运作。在你购买登山杖的时候，ItemCF通过计算与登山杖相似物品的相似度，最后发现登山鞋与登山杖最相似，最后ItemCF把登山鞋推荐给了你。

 ​ 根据上面的例子可知ItemCF算法的大致思路如下，首先计算出物品的相似度，然后根据相似度的大小和用户历史行为数据生成推荐列表。那么ItemCF是如何计算物品间的相似度，物品的形状？大小？材质？它的工作原理又是怎样的呢？

ItemCF的算法原理

 ​ 当然ItemCF算法并不是直接去根据物品的属性去直接去计算物品之间的相似度的，而是通过用户的行为间接计算物品之间的相似度。我们换个角度看，假设很多用户在买登山杖的同时也买了登山鞋，我们就可以认为这两个物品非常相似，从而得到如下的计算相似度的模型（1）：
$$W_{\mu v}=\frac{|N(\mu )\bigcap N(v)|}{|N(\mu )|}\text{\hspace{1em}(1)}$$
 ​ 模型（1）中分子部分|N(μ)∩N(v)|表示的含义是同时购买了物品μ和v的用户数量，如果购买了μ的同时都购买了v那么物品μ和v的相似度为1，分母中|N(μ)|代表的是购买了商品μ的用户总数。那么模型（1）还存在什么问题呢？我们假设商品v是一个非常热门的一个商品，这个时候v和任何商品相似度都会很高，从而导致ItemCF算法总是给用户推荐热门商品，因此我们需要对模型（1）进行优化，从而得到如下模型（2）：
$$W_{\mu v}=\frac{|N(\mu )\bigcap N(v)|}{\sqrt{|N(\mu )||N(v)|}}\text{\hspace{1em}(2)}$$
 ​ 模型（2）中在母部分做了变更，分母中|N(μ)||N(v)|表示购买了商品μ的用户数和购买了商品v的用户数的乘积。模型（2）对物品v加了惩罚，当N(v)比较大时分母也会比较大，从而降低了热门物品与其他物品相似的可能性。但是模型（2）依然存在一些问题，假设有一个用户他是卖服装的，他在App上买了200万件服装用于售卖，假设App平台有230万件服装，那么这200万件服装之间就产生了相似度，从而导致影响相似度的结果。我们可以认为购买物品的较多用户比购买物品较少的用户对相似度的贡献要低，从而提出如下模型：
$$W_{\mu v}=\frac{\sum _{i\in N(\mu )\bigcap N(v)}\frac{1}{log(1+|N(i)|)}}{\sqrt{|N(\mu )||N(v)|}}\text{\hspace{1em}(3)}$$
 ​ 模型（3）中在模型（2）的基础上对分子做了变更，N(μ)∩N(v)表示同时购买了μ和v的用户的集合，N(i)代表用户i购买的所有物品的总数，然后分别累加求和。最终我们得到优化的相似度计算模型，模型（3）被称作IUF（Inverse User Frequence） 算法。

​ 得到相似度计算模型后，我们要做的就是从多个相似的物品中挑选用户最感兴趣的物品。ItemCF主要是通过模型计算出用户对物品的感兴趣程度，计算模型如下：
$$P(u,\mu )=\sum _{v\in S(\mu ,K)\bigcap N(u)}{W}_{\mu v}{R}_{uv}$$
 ​ 上式中N(u)表示用户u喜欢的物品集合，S(μ，K)代表的是和物品μ最相似的k个物品的集合，W_μv表示物品μ和v的相似度，R_uv表示用户u对物品v的兴趣（假设购买过的R_uv=1，未购买过的R_uv=0）。最后根据P(u,μ)的大小进行逆序排列，取TopN作为推荐列表推荐给用户。

相似度归一化

 ​ 假设现在有两类商品A和B，A类物品之间的相似度为0.5，B类物品之间的相似度为0.7，A和B之间的相似度为0.2。在这样一个前提下如果一个用户喜欢了5个A类物品和5个B类物品，如果只推荐5个商品的话，由于B类之间的相似度很大，最终通过ItemCF算法推荐的物品都是B类物品。但是如果对相似度进行归一化之后，A类物品之间的相似度变成了1，B类物品之间的相似度也变成了1，这种情况下ItemCF算法推荐的A类物品和B类物品大致相等。因此，通过归一化可以提高推荐物品的多样性，提高推荐系统的覆盖率。归一化公式如下：

$$W_{ij}^{\prime }=\frac{w_{ij}}{\underset{j}{\max }(w_{ij})}$$

ItmeCF算法工作流程

 ​ 我们假设有数据集如下，以cosine相似度计算为例：

	物品
用户	a	b	c	d	e
U1	线性代数（a）	概率论（b）
U2			深度学习（c）		Python编程（e）
U3			深度学习（c）	数学之美（d）
U4		概率论（b）		数学之美（d）	Python编程（e）
U5	线性代数（a）			数学之美（d）

 ​ a.统计用户购买的列表

 ​  ​ {U1: {‘线性代数’, ‘概率论’}, U2: {‘深度学习’, ‘Python编程’}, U3: {‘深度学习’, ‘数学之美’}, U4: {‘概率论’, ‘数学之美’, ‘Python编程’}, U5: {‘线性代数’, ‘数学之美’}}

 ​ b.统计每个物品购买的用户数

 ​  ​ {‘线性代数’: 2, ‘概率论’: 2, ‘深度学习’: 2, ‘数学之美’: 3, ‘Python编程’: 2}

 ​ c.求解整体共现矩阵

求解整体共现矩阵过程
用户U1的共现矩阵 a b c d e a 0 1 0 0 0 b 1 0 0 0 0 c 0 0 0 0 0 d 0 0 0 0 0 e 0 0 0 0 0	用户U2的共现矩阵 a b c d e a 0 0 0 0 0 b 0 0 0 0 0 c 0 0 0 0 1 d 0 0 0 0 0 e 0 0 1 0 0	用户U3的共现矩阵 a b c d e a 0 0 0 0 0 b 0 0 0 0 0 c 0 0 0 1 0 d 0 0 1 0 0 e 0 0 0 0 0
用户U4的共现矩阵 a b c d e a 0 0 0 0 0 b 0 0 0 1 1 c 0 0 0 0 0 d 0 1 0 0 1 e 0 1 0 1 0	用户U5的共现矩阵 a b c d e a 0 0 0 1 0 b 0 0 0 0 0 c 0 0 0 0 0 d 1 0 0 0 0 e 0 0 0 0 0	整体共现矩阵 a b c d e a 0 1 0 1 0 b 1 0 0 1 1 c 0 0 0 1 1 d 1 1 1 0 1 e 0 1 1 1 0

​ d.计算相似矩阵
$$W_{ad}=W_{da}=\frac{|N(a)\bigcap N(d)|}{\sqrt{|N(a)||N(d)|}}=\frac{1}{\sqrt{2\ast 3}}=\frac{1}{\sqrt{6}}=0.4$$

$$W_{bd}=W_{db}=\frac{|N(b)\bigcap N(d)|}{\sqrt{|N(b)||N(d)|}}=\frac{1}{\sqrt{2\ast 3}}=\frac{1}{\sqrt{6}}=0.4$$

$$W_{ce}=W_{ec}=\frac{|N(c)\bigcap N(e)|}{\sqrt{|N(c)||N(e)|}}=\frac{1}{\sqrt{2\ast 2}}=\frac{1}{\sqrt{4}}=0.5$$

$$W_{cd}=W_{dc}=\frac{|N(c)\bigcap N(d)|}{\sqrt{|N(c)||N(d)|}}=\frac{1}{\sqrt{2\ast 3}}=\frac{1}{\sqrt{6}}=0.4$$

 ​ e.计算用户对物品感兴趣程度，以用户U3为例，U3用户购买了{深度学习（c）,数学之美(d)}，查找相似矩阵与用c相似的物品有{数学之美（d）, Python编程（e）}，与d物品相似的有{线性代数（a）, 概率论（b）, 深度学习（c）, Python编程（e）}，除去c和d最终推荐列表为{a, b, e}
$$P(U3,a)=W_{ca}{R}_{ca}+W_{da}{R}_{da}=W_{da}=0.4$$

$$P(U3,b)=W_{cb}{R}_{cb}+W_{db}{R}_{db}=W_{db}=0.4$$

$$P(U3,e)=W_{ce}{R}_{ce}+W_{de}{R}_{de}=W_{ce}+W_{de}=0.5+0.4=0.9$$

 ​ f.最后根据感兴趣程度倒排，如果推荐一个商品的话，那么最应该推的是商品Python编程（e）

代码实现

 ​ 代码中为了提升效率，使用嵌套字典模拟实现物品的共现矩阵

import itertools
from collections import Counter
from operator import itemgetter

from math import log1p, sqrt


def preprocess(data):
    """
    数据处理
    :param data: DataFrame数据
    :return:
    """
    user_items = {}
    items = data['item'].values
    for user, item in zip(data['user'].values, items):
        user_items.setdefault(user, set()).add(item)
    return user_items, Counter(items)


def cos(data):
    """
    计算余弦相似矩阵分子部分
    :param data:
    :return:
    """
    cos_mat = {}
    cos_setdefault, cos_get = cos_mat.setdefault, cos_mat.get
    for items in data.values():
        for y in items:
            cos_setdefault(y, {})
        items_len = len(items)
        if items_len > 1:
            for y, x in itertools.permutations(items, 2):
                cos_get(y).setdefault(x, 1) if cos_get(y).get(x) is None else cos_get(y).update(
                    {x: cos_get(y).get(x) + 1}
                )
    return cos_mat


def iuf(data):
    """
    改进后的相似矩阵分子部分
    :param data:
    :return:
    """
    iuf_mat = {}
    iuf_setdefault, iuf_get = iuf_mat.setdefault, iuf_mat.get
    for items in data.values():
        for y in items:
            iuf_setdefault(y, {})
        items_len = len(items)
        if items_len > 1:
            for y, x in itertools.permutations(items, 2):
                lg = 1. / log1p(items_len * 1.)
                iuf_get(y).setdefault(x, lg) if iuf_get(y).get(x) is None else iuf_get(y).update(
                    {x: iuf_get(y).get(x) + lg}
                )
    return iuf_mat


def co_matrix(train_data, func):
    """
    计算相似共现矩阵
    :param train_data:
    :param func:
    :return:
    """
    if func == 'iuf':
        return iuf(train_data)
    elif func == 'cos':
        return cos(train_data)


class ItemCF(object):

    def __init__(self, data, func='iuf', is_norm=False):
        self._train_data, self._item_count = preprocess(data)
        self._func = func
        self._sim_matrix = {}
        self._is_norm = is_norm

    def train(self):
        """
        计算相似度矩阵
        :return:
        """
        _train_data = self._train_data
        _func = self._func
        _item_count = self._item_count
        _sim_matrix = self._sim_matrix
        # 共现矩阵
        co_mat = co_matrix(_train_data, _func)
        # 计算相似度矩阵
        for i, co_sum in co_mat.items():
            _sim_matrix.setdefault(i, {})
            for j, cji in co_sum.items():
                _sim_matrix.get(i).setdefault(j, cji / sqrt(_item_count[i] * _item_count[j]))
        if self._is_norm:
            for i, relations in _sim_matrix.items():
                max_num = relations[max(relations, key=relations.get)]
                # 对字典进行归一化操作后返回新的字典
                _sim_matrix[i] = {k: v / max_num for k, v in relations.items()}

    def recommend(self, user, ton_n, scope):
        """
        推荐
        :param user: 需要推荐的用户
        :param ton_n: 推荐top_n列表
        :param scope: 查找范围
        :return:
        """
        recommend_list = {}
        _sim_matrix = self._sim_matrix
        items = self._train_data[user]
        for item in items:
            for i, sim in sorted(_sim_matrix[item].items(), key=itemgetter(1), reverse=True)[:scope]:
                if i in items:
                    continue
                val = recommend_list.get(i)
                recommend_list.setdefault(i, sim) if val is None else recommend_list.update({i: val + sim})
        return dict(sorted(recommend_list.items(), key=itemgetter(1), reverse=True)[:ton_n])

测试结果

 ​ 编写Test文件

from dmp.recommand.cus.cf import ItemCF
import pandas as pd

if __name__ == '__main__':
    good_label = pd.read_csv('data/test.csv')
    itemCF = ItemCF(good_label, 'cos')
    itemCF.train()
    recommend_list = itemCF.recommend('U3', ton_n=5, scope=5)
    print(recommend_list)

 ​ 运行结果如下图

总结

 ​ 优点：
 ​  ​ 模型简单，可解释性强，通过对用户和商品添加标签可以获得更好的精度
 ​  ​ 可以为具有特殊兴趣爱好的用户进行推荐
 ​ 缺点：
 ​  ​ 物品属性有限，难以区分商品信息的品质
 ​  ​ 模型相似度衡量的标准只考虑了物品本身，具有片面性
 ​  ​ 不能为用户发现新的感兴趣的产品

最后

 ​ 本人想组建一个技术交流群，有兴趣的可以扫码加入，用于学习和交流，希望和大家一起学习一起进步。
 ​  ​ QQ群：814507419

 ​  ​ 微信群：由于微信群二维码会失效，大家可以加我微信，然后拉大家进群期待和大家一起进步一起学习。微信号18397716181