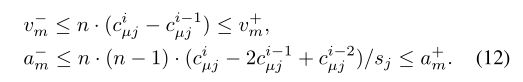Online Safe Trajectory Generation For Quadrotors Using Fast Marching Method and Bernstein Basis Poly
作者： 19届 lz
日期：2021-11-14
论文：《Online Safe Trajectory Generation For Quadrotors Using Fast Marching Method and Bernstein Basis Polynomial》
问题:
(a)第一个问题是分段轨迹的时间分配，选择不当的时间分配很容易产生低质量的轨迹。
(b)第二个问题是如何有效地约束自由空间内的整个轨迹及其导数在硬约束的可行空间内。
贡献:
(1)提出了一种基于欧氏距离场的快速推进方法，用于搜索时间指标路径，为轨迹优化提供合理的时间分配。
(2)一个轨迹优化框架，利用 bernstein 基生成平滑、安全、动态可行的轨迹。
(3)提出的运动规划方法和系统集成在一个完整的四旋翼平台上的实时实现。
一、背景：
在本文中，我们提出了一种四旋翼运动规划方法，不仅可以在未知环境中生成安全的，而且可以在动态范围内生成可行的轨迹。
二、有关工作：
三、研究过程及结果：
前端轨迹生成
快速行进算法:
是一种模拟波传播的方法，通过假设波阵面以 f 的速度沿其法向传播来计算波首次到达某一点的时间。假设传播速度 f > 0，即波阵面只向外发展，且具有时不变性，并且只依赖于空间中的位置.
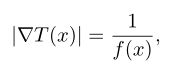
对于路径搜索，我们可以定义一个机器人导航的速度图。通过模拟从起点展开的波浪，得到地图上各点的到达时间。通过沿着到达时间梯度下降方向从目标点到达起点的路径追踪，得到了一条到达时间最短的路径。这就是在路径搜索中应用快速行进算法的主要思想。
与其他基于势场的方法不同，快速行进算法方法没有局部极小值。
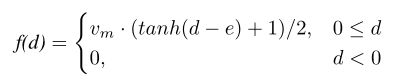
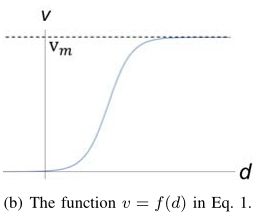
vm为最大速度, d为距离最近障碍物的距离
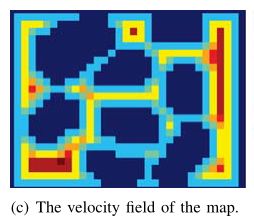
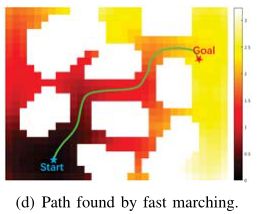
©表示地图中速度的分布,欧式符号距离场
(d)表示地图中,每个点到达的时间
启发式
d*(x): 表示x到目标点的欧氏距离
飞行走廊
在获得时间索引的最小到达路径后，提取环境中的自由空间，形成后端优化的飞行走廊。充分利用自由空间，因为寻找解空间和获得最优解对于轨迹生成同样重要。
首先通过欧式符号距离场,得到一个安全的空间球，初始化飞行走廊作为球体的内切立方体。然后我们通过查询轴对齐方向 x，y，z 最大的自由方向上的邻居网格来放大每个立方体
分析: 为什么要先初始化一个内切正方体?
可能是为了提高扩展速度，如果范围太大，就不用一层一层扩充了
后端轨迹优化
贝塞尔轨迹优化
贝塞尔曲线
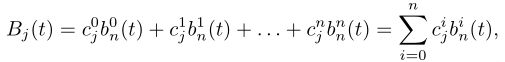
性质:
(1)经过第一个和最后一个控制点
(2)固定区间性质。参数t属于[0, 1]
(3)凸包性质。
(4)导数仍是贝塞尔曲线。
损失函数
因为是最小化jerk(加加速度), 所以k=3
si:比例因子,用于轨迹缩放
约束
对于每一段贝塞尔曲线，它的高阶导数可以用相应的低阶控制点的线性组合来表示
l:阶数
i:第几个控制点
u:x,y,z轴
j:控制点个数(阶)
路点约束
四旋翼飞行器需要通过的路径点,因为轨迹一定会经过第一个和最后一个控制点,所以通过路点约束,保证每段曲线之间的连接
连续性约束
保证每两段轨迹之间的连接是连续的
安全性约束
如上文, 如果保证控制点位于安全飞行走廊(凸包性质)中, 那么可以保证轨迹是无碰撞的
运动可行性约束
结果
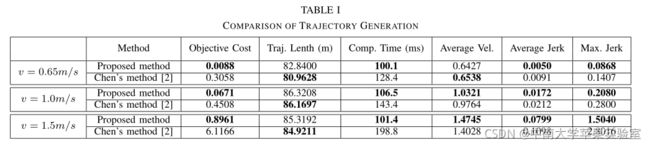
和chen方法区别:
(a)利用速度场中的快速行进算法来提供一个自然的时间索引路径，而不是根据一些启发式算法来搜索路径和分配时间.
(b)直接利用伯恩施坦多项式基来获得安全性和动力学可行性，这样就避免了碰撞风险。
conclusion
本文提出了一种用于四旋翼自主导航的在线运动规划框架。该方法采用一种快速的基于行进的路径搜索方法，在适应环境的速度场中找到一条基于时间指数化的路径。飞行走廊是基于路径生成和膨胀，以充分利用环境中的自由空间。最后，我们利用基于优化的方法来生成安全和动态可行的硬约束伯恩施坦多项式轨迹。