ADNet视频目标跟踪论文笔记
文章目录
- 1. 论文基本信息
- 2. 论文想要解决的问题
- 3. 核心思想
- 4. 数学符号
- 5. 重要概念及定义
-
- 5.1 Action
- 5.2 State
- 5.3 状态转移函数(State transition function)
- 5.4 奖励(Reward)
- 6. 网络结构
- 7. Off-line Supervised Learning
- 8. Off-line Reinforcement Learning
-
- 8.1 模拟跟踪(tracking simulation)
- 8.2 动作迭代
- 8.3 强化学习建模
- 8.4 RL算法描述
- 9. Online Adaptation
- 10. 总结
1. 论文基本信息
- 论文标题:Action-Decision Networks for Visual Tracking with Deep Reinforcement Learning
- 论文作者:Sangdoo Yun(Seoul National University, South Korea)等人
- 论文出处:CVPR 2017
- 在线阅读:http://openaccess.thecvf.com/content_cvpr_2017/papers/Yun_Action-Decision_Networks_for_CVPR_2017_paper.pdf
- 补充材料:http://openaccess.thecvf.com/content_cvpr_2017/supplemental/Yun_Action-Decision_Networks_for_2017_CVPR_supplemental.pdf
- 源码链接1:https://github.com/hellbell/ADNet (MATLAB版本)
- 源码链接2:https://github.com/ildoonet/tf-adnet-tracking (TensorFlow版本)
2. 论文想要解决的问题
当前大多数深度学习的跟踪算法存在如下两方面不足:
- 算法没能有效地去选择候选样本,具有一定的盲目性。例如MDNet算法就进行了密集采样,然后输出得分,选择最高得分的样本作为目标图像,这样做的不足之处在于做了一些不必要的样本搜索,浪费了不必要的时间。
- 在训练深度网络时需要依赖大量的标记数据,在半监督模式下无法使用未标记的视频帧。使用传统的深度学习跟踪方法在实际应用中,仅仅利用公开的标注数据集可能不够,特别是在特定应用场景下需要自己建立标注数据集,这样比较耗时费力。
3. 核心思想
为解决上述第一点不足,作者提出利用action-driven机制来捕获目标物体的运动信息,这样可以保证优先搜索到更高质量的候选样本。为解决上述第二点不足,作者采用强化学习方法在部分标记的数据集上进行训练,训练出前面提及的action-driven模型。
论文的核心思想如下图所示:

从上图可以看出,论文的核心思想就是Action-decision,即通过不同的动作来进行连续采样,并最终定位到目标的位置。
4. 数学符号
本文的数学符号较多,在这里先建立一个数学符号表格备查,如下所示:
| 符号 | 含义 |
|---|---|
| l l l | 帧号 |
| t t t | 迭代次数 |
| s t s_t st | 第 t t t次迭代后的状态 |
| p t p_t pt | 第 t t t次迭代时的图像块 |
| d t d_t dt | 第 t t t次迭代时的动作动态(action dynamics),它包含过去的 k k k次历史行为 |
| b t b_t bt | 第 t t t次迭代初始时的bounding-box |
| m m m (from 论文Figure. 2) | 可选的 m m m种动作,对于本文, m = 11 m=11 m=11(即论文Figure. 3中定义的11种action) |
| m m m (from 论文Eq. (6)) | training过程中一个batch的样本数量 |
| F F F | 完整的视频画面图像 |
| a t − 1 a_{t-1} at−1 | 第 t − 1 t-1 t−1次迭代的动作(action) |
| Δ x ( t ) \Delta {x^{\left( t \right)}} Δx(t), Δ y ( t ) \Delta {y^{\left( t \right)}} Δy(t) | 第 t t t次迭代时,在 x x x和 y y y两个方向上的试探位移量 |
| r ( s t ) r\left( {{s_t}} \right) r(st) | 第 t t t次迭代后得到的奖励,在迭代过程中该数值为0 |
| W W W | 深度网络权重 |
| p ( a p(a p(a | s t ; W ) s_t;W) st;W) | 给定状态 s t s_t st下的行为概率(action probability) |
| p ( t a r g e t p(target p(target | s t ; W ) s_t;W) st;W) | 给定状态 s t s_t st下,对应图像块是目标的概率 |
| { F l } l = 1 L \left \{ F_l \right \}_{l=1}^{\mathcal{L}} {Fl}l=1L 和 { G l } l = 1 L \left \{ G_l \right \}_{l=1}^{\mathcal{L}} {Gl}l=1L | 随机选择的一段视频帧画面以及对应的ground-truths |
| { u l } l = 1 L \left \{ u_l \right \}_{l=1}^{\mathcal{L}} {ul}l=1L | 随机选择的一段视频帧数据,其中 u l = { s t , l , a t , l } t = 1 T l u_l = \left \{ s_{t,l}, a_{t,l} \right \}_{t=1}^{T_l} ul={st,l,at,l}t=1Tl |
| T l T_l Tl | 在RL训练过程中,第 l l l帧内部的迭代步数 |
| z t , l z_{t,l} zt,l | 跟踪结果得分。论文用IoU指标计算该得分,并将该得分作为奖励 |
注: 文本中一共有两处出现了字母 m m m,它们代表了不同的含义:一处出现在示意图中,它表示action score向量的维数;另一处出现在论文的4.1节中,它表示batch的size。
5. 重要概念及定义
5.1 Action
Action是指强化学习代理的行为。在ADNet跟踪算法中,一共设置了11种行为,它们分为三类:移动、缩放和停止,如下图所示:

5.2 State
State指的是强化学习代理采取某种行为后的状态。在ADNet论文中,算法在每一帧中都会迭代多次,其中每迭代一次,就会执行上述某种行为,进而就会更新一次状态。其公式如下所示:
s t = ( p t , d t ) = ( ϕ ( b t , F ) , [ φ ( a t − 1 ) , φ ( a t − 2 ) , … , φ ( a t − k ) ] ) (1) \begin{aligned} {s_t} &= \left( {{p_t},{d_t}} \right) \\ &= \left( {\phi \left( {{b_t},F} \right),\left[ {\varphi \left( {{a_{t - 1}}} \right),\varphi \left( {{a_{t - 2}}} \right), \ldots ,\varphi \left( {{a_{t - k}}} \right)} \right]} \right) \\ \end{aligned} \tag {1} st=(pt,dt)=(ϕ(bt,F),[φ(at−1),φ(at−2),…,φ(at−k)])(1)
其中, p t p_t pt表示每一次迭代得到的图像块, d t d_t dt表示行为动态(action dynamics),它包含过去的 k k k次历史行为。
5.3 状态转移函数(State transition function)
这里的状态转移主要包括两点内涵:图像块的转移和action dynamics的转移。图像块的转移是指:在当前状态下,因为采取了某种动作(平移、缩放等),使得采样的图像块发生了变化。action dynamics的转移是指:因为采取了动作, d t d_t dt的内容会发生更新(因为进来了新的动作记录)。
5.4 奖励(Reward)
在强化学习过程中,论文对每一个状态 s t s_t st计算奖励 r ( s t ) r(s_t) r(st),其计算公式为:
r ( s t ) = { 1 if I o U ( b t , G ) > 0.7 − 1 otherwise (2) r\left ( s_t \right ) = \begin{cases} 1 & \text{ if } IoU\left ( b_t,G \right )>0.7 \\ -1 & \text{ otherwise } \end{cases} \tag {2} r(st)={1−1 if IoU(bt,G)>0.7 otherwise (2)
其中 b t b_t bt是状态 s t s_t st时采样的图像块, G G G表示ground-truth。
6. 网络结构
ADNet跟踪算法的网络结构如下图所示:

从图中可以看出,网络的核心部分是一个VGG-m卷积神经网络,只是本文网络结构的特色在于,在fc5全连接之后的输出结果concat了一个 m × k m \times k m×k维的向量(对应了 m m m种动作, k k k个历史记录)。
在作者给出的官方MATLAB源码中,可以发现其完整的网络结构如下图所示:

上图中,fc6_2其实就是论文建模中的fc7 layer,可以将它理解为动作分类器,即根据输入的图像块决定应该采取何种action来尽可能地靠近目标。
7. Off-line Supervised Learning
在离线监督学习阶段,算法训练所有的网络权重(即 w 1 , w 2 , w 3 , … , w 7 \mathbf{w}_1, \mathbf{w}_2, \mathbf{w}_3, \dots, \mathbf{w}_7 w1,w2,w3,…,w7)(这里的 w 7 \mathbf{w}_7 w7即为MATLAB源码网络中的fc6_2 layer),训练的样本由算法生成出来,每一个training样本包含如下三种信息:
- 图像块 { p j } \left \{ p_j \right \} {pj}
- 动作标签 { o j ( a c t ) } \left \{ o_{j}^{\left ( act \right )} \right \} {oj(act)}
- 类别标签 { o j ( c l s ) } \left \{ o_{j}^{\left ( cls \right )} \right \} {oj(cls)}
其中,上述动作标签 o j ( a c t ) o_{j}^{\left ( act \right )} oj(act)的定义为:
o j ( a c t ) = arg max a I o U ( f ˉ ( p j , a ) , G ) (3) o_{j}^{\left ( act \right )} = \text{arg} \underset{a}{\text{max}}IoU\left ( \bar{f}\left ( p_j,a \right ),G \right ) \tag {3} oj(act)=argamaxIoU(fˉ(pj,a),G)(3)
上面的公式中, G G G是指ground-truth的图像块, f ˉ ( p j , a ) \bar{f}\left ( p_j,a \right ) fˉ(pj,a)的含义是:在当前图像块 p j p_j pj的基础上,执行动作 a a a,于是得到一个新的图像采样 f ˉ ( p j , a ) \bar{f}\left ( p_j,a \right ) fˉ(pj,a)。对于这样的动作,我们会执行多种,因此也会得到多个新的图像块。对于得到的每一种图像块,我们都会计算它与ground-truth图像块的IoU数值,取具有最大IoU图像块对应的动作 a a a作为当前training样本的动作标签。
类别标签 o j ( c l s ) o_{j}^{\left ( cls \right )} oj(cls)的定义为:
o j ( c l s ) = { 1 if I o U ( p j , G ) > 0.7 0 otherwise (4) o_{j}^{\left ( cls \right )} = \begin{cases} 1 & \text{ if } IoU\left ( p_j,G \right )>0.7 \\ 0 & \text{ otherwise } \end{cases} \tag {4} oj(cls)={10 if IoU(pj,G)>0.7 otherwise (4)
在supervised learning阶段,算法采用随机梯度下降(stochastic gradient descent,SGD)来训练网络权重,其对应的损失函数是一个multi-task loss function,如下所示(带hat符号的表示网络的预测值, m m m表示一个batch的大小):
L S L = 1 m ∑ j = 1 m L ( o j ( a c t ) , o ^ j ( a c t ) ) + 1 m ∑ i = j m L ( o j ( c l s ) , o ^ j ( c l s ) ) (5) L_{SL} = \frac{1}{m}\sum_{j=1}^{m}L\left ( o_{j}^{(act)},\hat{o}_j^{(act)} \right )+\frac{1}{m}\sum_{i=j}^{m}L\left ( o_{j}^{(cls)},\hat{o}_j^{(cls)} \right ) \tag {5} LSL=m1j=1∑mL(oj(act),o^j(act))+m1i=j∑mL(oj(cls),o^j(cls))(5)
从上面的公式可以看出,supervised learning包含两个任务:对动作的损失计算以及对分类的损失计算,两者之和即构成了监督学习阶段的loss function。值得一提的是,尽管这里的损失函数已经应用了动作的概念,但这部分并不属于真正意义上的强化学习,因为这里既没有用到类似于Q-learning,也没有策略梯度等求解方法,这部分的损失函数定义与大多数深度学习方法相同,都是属于直接利用label值的差异来进行定义。
8. Off-line Reinforcement Learning
离线强化学习阶段紧跟着上述supervised learning之后进行,在这一阶段,算法仅仅训练网络权重中的 w 1 , w 2 , w 3 , … , w 6 \mathbf{w}_1, \mathbf{w}_2, \mathbf{w}_3, \dots, \mathbf{w}_6 w1,w2,w3,…,w6,不训练 w 7 \mathbf{w}_7 w7(即:不训练prediction score前面的fc layer),在这一阶段,论文使用的强化学习方法为policy gradient(R. J. Williams. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine learning, 8(3-4):229–256, 1992. 2,3,5,在线阅读)。
8.1 模拟跟踪(tracking simulation)
在RL阶段中,论文随机地截取一段训练视频 { F l } l = 1 L \left \{ F_l \right \}_{l=1}^{\mathcal{L}} {Fl}l=1L以及对应的ground-truth { G l } l = 1 L \left \{ G_l \right \}_{l=1}^{\mathcal{L}} {Gl}l=1L,对于这一段视频,论文采用了一种模拟跟踪(tracking simulation)的方法来进行深度强化学习,这种方法带有半监督性质,具体是指:在截取的一段视频中,让算法自由跟踪目标一段时间,当到达某一个关键帧时(对于关键帧,需要利用该帧的ground-truth信息),评估跟踪的结果并计算奖励 R R R。其主要过程如下图所示(红色矩形框为ground-truth,蓝色矩形框为算法模拟跟踪的结果):

从上图可以看出,在第160帧至第190帧,算法自由跟踪目标物体,并且在第190帧时利用ground-truth信息对跟踪质量进行评价,得到了+1分的奖励(因为第190帧时算法基本上准确地定位了目标)。从第190帧到第220帧,算法得到的奖励为-1分(因为在第220帧时算法丢失了目标)。
注: 尽管论文的训练视频数据是每一帧都带有ground-truth的,但算法在进行模拟跟踪期间,出了关键帧以外,即使有其他帧的标注,算法也不会去用。
模拟跟踪部分的代码如下所示(跟踪 + 评价):
for frameIdx = frameStart+1:frameEnd
curr_img = imread(fullfile(vid_info.img_files(frameIdx).name));
if(size(curr_img,3)==1), curr_img = cat(3,curr_img,curr_img,curr_img); end
curr_gt_bbox = vid_info.gt(frameIdx,:);
[curr_bbox, action_history, ~, ~, ims, actions, ah_onehot, ~] = ...
tracker_rl(curr_img, curr_bbox, net_conv, net_fc, action_history, opts);
ah_onehots = cat(2, ah_onehots, ah_onehot);
imgs = cat(4, imgs, ims);
action_labels = cat(1, action_labels, actions);
end
% target value (z)
if overlap_ratio(curr_gt_bbox, curr_bbox) > 0.7
ah_pos = cat(2, ah_pos, ah_onehots);
imgs_pos = cat(4, imgs_pos, imgs);
action_labels_pos = cat(1, action_labels_pos, action_labels);
else
ah_neg = cat(2, ah_neg, ah_onehots);
imgs_neg = cat(4, imgs_neg, imgs);
action_labels_neg = cat(1, action_labels_neg, action_labels);
end
从上述代码可以看出,算法在模拟跟踪期间主要依赖RL阶段的专用自由跟踪函数tracker_rl(curr_img, curr_bbox, net_conv, net_fc, action_history, opts),在跟踪过程中不进行任何评价,因此也不需要使用标注的ground-truth信息,当这一段视频的自由跟踪结束才会利用IoU指标进行评价,并且仅仅评价最后一帧的结果。这里也体现出了论文的第二个研究动机:大多数传统tracking算法在训练深度网络时需要依赖大量的标记数据,在半监督模式下无法使用未标记的视频帧。
8.2 动作迭代
研究动作迭代,需要弄清楚三个问题:
- 什么地方需要用到动作迭代?
- 迭代时如何选择动作,其依据是什么?
- 何时停止迭代?
首先回答第一个问题。动作迭代用于tracking行为,不仅在RL训练阶段会用到动作迭代的方法,并且在真正的testing阶段也会用到动作迭代方法。
由于RL阶段的任务非常明确:就是学习一套找到目标的策略(对于本文而言,策略包含一系列的动作,因此在RL阶段会涉及到迭代,这也是RL阶段与SL阶段不同的地方。),论文在这里提出了一个动作动态( action dynamics)的概念,其作用是存储过去迭代步骤中的动作集合,用 d t d_t dt进行表示:
d t = [ ψ ( a t − 1 ) , ψ ( a t − 2 ) , … , ψ ( a t − k ) ] (6) d_t=\left [ \psi \left ( a_{t-1} \right ) , \psi \left ( a_{t-2} \right ) , \dots, \psi \left ( a_{t-k} \right ) \right ] \tag {6} dt=[ψ(at−1),ψ(at−2),…,ψ(at−k)](6)
这里,论文将 k k k设置为10,再考虑到每一次迭代都有11种action可以选择,于是 d t d_t dt为一个110维的向量。里面的 ψ ( ⋅ ) \psi( \cdot) ψ(⋅)表示one-hot编码函数,对采取的那一种动作编码1,对其他动作编码0。
在模拟跟踪(tracking simulation)的过程中,为了达到定位的目的,每一帧内部包含多次动作迭代。 而其中每一次迭代都会选择一个动作 a t , l a_{t,l} at,l,其动作选择公式为:
a t , l = arg max a p ( a ∣ s t , l ; W R L ) (7) a_{t,l}=\text{arg}\underset{a}{\text{max}}p\left ( a \mid s_{t,l}; W_{RL} \right ) \tag {7} at,l=argamaxp(a∣st,l;WRL)(7)
上面这个公式的意思是:在当前网络的权重条件,以及第 l l l帧画面中的第 t t t次迭代的状态下,具有最大输出概率的动作 a a a即为当前迭代要采取的动作。这里如何理解 p ( a ∣ s t , l ; W R L ) p\left ( a \mid s_{t,l}; W_{RL} \right ) p(a∣st,l;WRL)?因为论文设计的网络输出中,对于fc6_1这一层的动作得分输出是一个11维的向量,它包含11个元素,其中每一个元素表示对应action的概率,如下图所示:
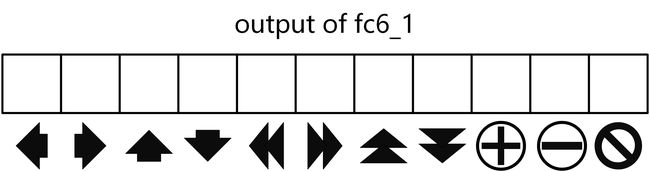
这样算法在执行时,每一次迭代只需要选择具有最高得分所对应的action即可。
RL阶段中的动作迭代代码如下所示:
while (move_counter <= num_action_step_max)
bb_step(move_counter,:) = curr_bbox;
my_net_conv.mode = 'test';
[curr_feat_conv, im] = get_conv_feature(my_net_conv, curr_img, curr_bbox, opts);
ims(:,:,:, move_counter) = im;
conv_feats(:,:,:, move_counter) = curr_feat_conv;
curr_feat_conv = gpuArray(curr_feat_conv);
my_net_fc.mode = 'test';
labels = zeros(1);
ah_oh = get_action_history_onehot(action_history(1:opts.num_action_history), opts);
ah_oh = reshape(ah_oh, [1,1,numel(ah_oh),1]);
ah_onehot(:,move_counter) = ah_oh;
inputs = {'x10', curr_feat_conv, 'action_history', gpuArray( ah_oh)};
my_net_fc.eval(inputs);
my_net_pred = squeeze(gather(my_net_fc.getVar('prediction').value));
my_net_pred_score = squeeze(gather(my_net_fc.getVar('prediction_score').value));
curr_score = my_net_pred_score(2);
[~, my_net_max_action] = max(my_net_pred(1:end));
if (prev_score < -5.0 && curr_score < prev_score)
if randn(1) < 0.5
my_net_max_action = randi(11);
end
end
actions(move_counter) = my_net_max_action;
curr_bbox = do_action(curr_bbox, opts, my_net_max_action, imSize);
% when come back again (oscillating)
[~, ism] = ismember(round(bb_step), round(curr_bbox), 'rows');
if sum(ism) > 0 ...
&& my_net_max_action ~= opts.stop_action
my_net_max_action = opts.stop_action;
end
action_history(2:end) = action_history(1:end-1);
action_history(1) = my_net_max_action;
this_actions(move_counter) = 1;
if my_net_max_action == opts.stop_action
break;
end
move_counter = move_counter + 1;
prev_score = curr_score;
end
从上述代码中可以发现,动作迭代的停止条件有两个:1) 如果迭代到了停止动作,就停止迭代;2) 如果超过了最大的迭代次数,就停止迭代。
8.3 强化学习建模
综上,我们得到了action选择方法,有了奖励计算公式,此时可以进行策略梯度(policy gradient)的强化学习建模,首先建立目标函数:
J ( W R L ) = E u l ∼ p ( u l ; W R L ) [ R ( u l ) ] = ∑ u l ∈ U p ( u l ; W R L ) ⋅ R ( u l ) = ∑ u l ∈ U p ( u l ; W R L ) ⋅ 1 T l ∑ t T l z t , l = ∑ u l ∈ U p ( u l ; W R L ) ⋅ z T l , l (8) \begin{aligned} J\left ( W_{RL} \right )&= \mathbb{E}_{u_{l} \sim p\left (u_{l};W_{RL} \right)} \left [ R\left ( u_{l} \right ) \right ] \\ &= \sum_{u_{l} \in \mathbb{U}} p\left ( u_{l}; W_{RL} \right ) \cdot R\left ( u_{l} \right ) \\ &= \sum_{u_{l} \in \mathbb{U}} p\left ( u_{l}; W_{RL} \right ) \cdot \frac{1}{T_l}\sum_{t}^{T_l} z_{t,l} \\ &= \sum_{u_{l} \in \mathbb{U}} p\left ( u_{l}; W_{RL} \right ) \cdot z_{T_l,l} \end{aligned} \tag {8} J(WRL)=Eul∼p(ul;WRL)[R(ul)]=ul∈U∑p(ul;WRL)⋅R(ul)=ul∈U∑p(ul;WRL)⋅Tl1t∑Tlzt,l=ul∈U∑p(ul;WRL)⋅zTl,l(8)
论文用 { u l } l = 1 L \left \{ u_l \right \}_{l=1}^{\mathcal{L}} {ul}l=1L表示随机选择的一段视频帧数据,其中 u l u_l ul只是这一段视频中的一帧,而它的内部又包含了 T l T_l Tl个元素,每一个元素对应一次动作迭代:
u l = { s t , l , a t , l } t = 1 T l (9) u_l = \left \{ s_{t,l}, a_{t,l} \right \}_{t=1}^{T_l} \tag {9} ul={st,l,at,l}t=1Tl(9)
所有可能的帧的集合就是 U \mathbb{U} U, p ( u l ; W R L ) p\left ( u_{l}; W_{RL} \right ) p(ul;WRL)表示在当前的网络权重 W R L W_{RL} WRL条件下,第 l l l帧选择的动作概率分布, R ( u l ) R\left ( u_{l} \right ) R(ul)表示第 l l l帧的奖励。
z t , l z_{t,l} zt,l表示跟踪结果得分,论文用IoU指标计算该得分,并将该得分作为奖励。
这样的形式化表述也从侧面说明了:在论文的设计方案中,RL的训练只涉及一部分视频帧,而每一帧内都会进行多次动作迭代。
上述目标函数公式的最后两行很关键,这里再重复写一下:
J ( W R L ) = ∑ u l ∈ U p ( u l ; W R L ) ⋅ 1 T l ∑ t T l z t , l = ∑ u l ∈ U p ( u l ; W R L ) ⋅ z T l , l (10) \begin{aligned} J\left ( W_{RL} \right ) &= \sum_{u_{l} \in \mathbb{U}} p\left ( u_{l}; W_{RL} \right ) \cdot \frac{1}{T_l}\sum_{t}^{T_l} z_{t,l} \\ &= \sum_{u_{l} \in \mathbb{U}} p\left ( u_{l}; W_{RL} \right ) \cdot z_{T_l,l} \end{aligned} \tag {10} J(WRL)=ul∈U∑p(ul;WRL)⋅Tl1t∑Tlzt,l=ul∈U∑p(ul;WRL)⋅zTl,l(10)
为何 1 T l ∑ t T l z t , l = z T l , l \frac{1}{T_l}\sum_{t}^{T_l} z_{t,l} = z_{T_l,l} Tl1∑tTlzt,l=zTl,l?这是因为根据论文的模拟跟踪(tracking simulation)机制,在计算奖励时,仅仅使用关键帧的标注信息。即:仅仅在关键帧才计算奖励。
利用Markov假设,这里目标函数中的 p ( u l ; W R L ) p\left ( u_{l}; W_{RL} \right ) p(ul;WRL)可以写成:
p ( u l ; W R L ) = p ( s 1 , l ) Π t = 1 T p ( s t + 1 , l ∣ s t , l , a t , l ) p ( a t , l ∣ s t , l ; W R L ) = [ p ( s T + 1 , l ∣ s T , l , a T , l ) p ( a T , l ∣ s T , l ; W R L ) ] ⋅ [ p ( s T , l ∣ s T − 1 , l , a T − 1 , l ) p ( a T − 1 , l ∣ s T − 1 , l ; W R L ) ] ⋅ … [ p ( s 4 , l ∣ s 3 , l , a 3 , l ) p ( a 3 , l ∣ s 3 , l ; W R L ) ] ⋅ [ p ( s 3 , l ∣ s 2 , l , a 2 , l ) p ( a 2 , l ∣ s 2 , l ; W R L ) ] ⋅ [ p ( s 2 , l ∣ s 1 , l , a 1 , l ) p ( a 1 , l ∣ s 1 , l ; W R L ) ] ⋅ p ( s 1 , l ) (11) \begin{array}{l} \;\;\;\;p\left( {{u_l};{W_{RL}}} \right)\\ = p\left( {{s_{1,l}}} \right)\Pi _{t = 1}^Tp\left( {{s_{t + 1,l}}\left| {{s_{t,l}},{a_{t,l}}} \right.} \right)p\left( {{a_{t,l}}\left| {{s_{t,l}};{W_{RL}}} \right.} \right)\\ = \left[ {p\left( {{s_{T + 1,l}}\left| {{s_{T,l}},{a_{T,l}}} \right.} \right)p\left( {{a_{T,l}}\left| {{s_{T,l}};{W_{RL}}} \right.} \right)} \right] \cdot \\ \;\;\;\;\left[ {p\left( {{s_{T,l}}\left| {{s_{T - 1,l}},{a_{T - 1,l}}} \right.} \right)p\left( {{a_{T - 1,l}}\left| {{s_{T - 1,l}};{W_{RL}}} \right.} \right)} \right] \cdot \\ \;\;\;\; \ldots \\ \;\;\;\;\left[ {p\left( {{s_{4,l}}\left| {{s_{3,l}},{a_{3,l}}} \right.} \right)p\left( {{a_{3,l}}\left| {{s_{3,l}};{W_{RL}}} \right.} \right)} \right] \cdot \\ \;\;\;\;\left[ {p\left( {{s_{3,l}}\left| {{s_{2,l}},{a_{2,l}}} \right.} \right)p\left( {{a_{2,l}}\left| {{s_{2,l}};{W_{RL}}} \right.} \right)} \right] \cdot \\ \;\;\;\;\left[ {p\left( {{s_{2,l}}\left| {{s_{1,l}},{a_{1,l}}} \right.} \right)p\left( {{a_{1,l}}\left| {{s_{1,l}};{W_{RL}}} \right.} \right)} \right] \cdot \\ \;\;\;\;p\left( {{s_{1,l}}} \right) \end{array} \tag {11} p(ul;WRL)=p(s1,l)Πt=1Tp(st+1,l∣st,l,at,l)p(at,l∣st,l;WRL)=[p(sT+1,l∣sT,l,aT,l)p(aT,l∣sT,l;WRL)]⋅[p(sT,l∣sT−1,l,aT−1,l)p(aT−1,l∣sT−1,l;WRL)]⋅…[p(s4,l∣s3,l,a3,l)p(a3,l∣s3,l;WRL)]⋅[p(s3,l∣s2,l,a2,l)p(a2,l∣s2,l;WRL)]⋅[p(s2,l∣s1,l,a1,l)p(a1,l∣s1,l;WRL)]⋅p(s1,l)(11)
现在,我们求解目标函数 J ( W R L ) J\left( W_{RL} \right) J(WRL)的偏导数,有:
∇ W R L J ( W R L ) = ∑ u l ∈ U ∇ W R L p ( u l ; W R L ) R ( u l ) (12) {\nabla _{{W_{RL}}}}J\left( {{W_{RL}}} \right) = \sum\limits_{{u_l} \in U} {{\nabla _{{W_{RL}}}}p\left( {{u_l};{W_{RL}}} \right)R\left( {{u_l}} \right)} \tag {12} ∇WRLJ(WRL)=ul∈U∑∇WRLp(ul;WRL)R(ul)(12)
在公式中,论文使用对数似然
∇ W R L log p ( u l ; W R L ) = 1 p ( u l ; W R L ) ⋅ ∇ W R L p ( u l ; W R L ) (13) {\nabla _{{W_{RL}}}}\log p\left( {{u_l};{W_{RL}}} \right) = \frac{1}{{p\left( {{u_l};{W_{RL}}} \right)}} \cdot {\nabla _{{W_{RL}}}}p\left( {{u_l};{W_{RL}}} \right) \tag {13} ∇WRLlogp(ul;WRL)=p(ul;WRL)1⋅∇WRLp(ul;WRL)(13)
于是目标函数的偏导数可以写成:
∇ W R L J ( W R L ) = ∑ u l ∈ U ∇ W R L p ( u l ; W R L ) R ( u l ) = ∑ u l ∈ U p ( u l ; W R L ) ⋅ ∇ W R L log p ( u l ; W R L ) R ( u l ) = E u l ∼ p ( u l ; W R L ) [ ∇ W R L log p ( u l ; W R L ) R ( u l ) ] (14) \begin{aligned} {\nabla _{{W_{RL}}}}J\left( {{W_{RL}}} \right) &= \sum\limits_{{u_l} \in U} {{\nabla _{{W_{RL}}}}p\left( {{u_l};{W_{RL}}} \right)R\left( {{u_l}} \right)} \\ &= \sum\limits_{{u_l} \in U} {p\left( {{u_l};{W_{RL}}} \right) \cdot {\nabla _{{W_{RL}}}}\log p\left( {{u_l};{W_{RL}}} \right)R\left( {{u_l}} \right)} \\ &= {\mathbb{E}_{{u_l} \sim p\left( {{u_l};{W_{RL}}} \right)}}\left[ {{\nabla _{{W_{RL}}}}\log p\left( {{u_l};{W_{RL}}} \right)R\left( {{u_l}} \right)} \right] \end{aligned} \tag {14} ∇WRLJ(WRL)=ul∈U∑∇WRLp(ul;WRL)R(ul)=ul∈U∑p(ul;WRL)⋅∇WRLlogp(ul;WRL)R(ul)=Eul∼p(ul;WRL)[∇WRLlogp(ul;WRL)R(ul)](14)
将公式(11)代入到上式,并忽略掉与 W R L W_{RL} WRL无关的项,得:
∇ W R L J ( W R L ) = E u l ∼ p ( u l ; W R L ) [ ∇ W R L log p ( u l ; W R L ) R ( u l ) ] = E u l ∼ p ( u l ; W R L ) [ ∇ W R L log [ p ( s 1 , l ) Π t = 1 T l p ( s t + 1 , l ∣ s t , l , a t , l ) p ( a t , l ∣ s t , l ; W R L ) ] ⋅ R ( u l ) ] = E u l ∼ p ( u l ; W R L ) [ ∇ W R L log [ p ( s 1 , l ) Π t = 1 T l p ( s t + 1 , l , a t , l ; W R L ) ] ⋅ R ( u l ) ] = E u l ∼ p ( u l ; W R L ) [ ∇ W R L [ log p ( s 1 , l ) + ∑ t = 1 T l log p ( s t + 1 , l , a t , l ; W R L ) ] ⋅ R ( u l ) ] ∝ E u l ∼ p ( u l ; W R L ) [ ∇ W R L [ log p ( s 1 , l ) + ∑ t = 1 T l log p ( s t + 1 , l , a t , l ; W R L ) ] ⋅ R ( u l ) ] ≈ E u l ∼ p ( u l ; W R L ) [ ∇ W R L ∑ t = 1 T l log p ( s t + 1 , l , a t , l ; W R L ) ⋅ R ( u l ) ] = E u l ∼ p ( u l ; W R L ) [ ∑ t = 1 T l ∇ W R L log p ( s t + 1 , l , a t , l ; W R L ) ⋅ R ( u l ) ] = ∑ u l ∈ U p ( u l ; W R L ) ⋅ [ ∑ t = 1 T l ∇ W R L log p ( s t + 1 , l , a t , l ; W R L ) ⋅ R ( u l ) ] = ∑ l L p ( u l ; W R L ) ⋅ [ ∑ t = 1 T l ∇ W R L log p ( s t + 1 , l , a t , l ; W R L ) ⋅ R ( u l ) ] = ∑ l L ∑ t = 1 T l p ( u l ; W R L ) ⋅ ∇ W R L log p ( s t + 1 , l , a t , l ; W R L ) ⋅ R ( u l ) ≈ 1 L ∑ l L ∑ t = 1 T l ∇ W R L log p ( s t + 1 , l , a t , l ; W R L ) ⋅ R ( u l ) ≈ 1 L ∑ l L ∑ t = 1 T l ∇ W R L log p ( a t , l , s t + 1 , l ; W R L ) ⋅ R ( u l ) ( 本 文 得 出 的 推 导 结 果 ) ≈ 1 L ∑ l L ∑ t = 1 T l ∇ W R L log p ( a t , l , s t , l ; W R L ) ⋅ R ( u l ) ( 论 文 得 出 的 推 导 结 果 ) (15) \begin{aligned} {\nabla _{{W_{RL}}}}J\left( {{W_{RL}}} \right) &= {\mathbb{E}_{{u_l} \sim p\left( {{u_l};{W_{RL}}} \right)}}\left[ {{\nabla _{{W_{RL}}}}\log p\left( {{u_l};{W_{RL}}} \right)R\left( {{u_l}} \right)} \right]\\ &= {\mathbb{E}_{{u_l} \sim p\left( {{u_l};{W_{RL}}} \right)}}\left[ {{\nabla _{{W_{RL}}}}\log \left[ {p\left( {{s_{1,l}}} \right)\Pi _{t = 1}^{{T_l}}p\left( {{s_{t + 1,l}}\left| {{s_{t,l}},{a_{t,l}}} \right.} \right)p\left( {{a_{t,l}}\left| {{s_{t,l}};{W_{RL}}} \right.} \right)} \right] \cdot R\left( {{u_l}} \right)} \right]\\ &= {\mathbb{E}_{{u_l} \sim p\left( {{u_l};{W_{RL}}} \right)}}\left[ {{\nabla _{{W_{RL}}}}\log \left[ {p\left( {{s_{1,l}}} \right)\Pi _{t = 1}^{{T_l}}p\left( {{s_{t + 1,l}},{a_{t,l}};{W_{RL}}} \right)} \right] \cdot R\left( {{u_l}} \right)} \right]\\ &= {\mathbb{E}_{{u_l} \sim p\left( {{u_l};{W_{RL}}} \right)}}\left[ {{\nabla _{{W_{RL}}}}\left[ {\log p\left( {{s_{1,l}}} \right) + \sum\limits_{t = 1}^{{T_l}} {\log p\left( {{s_{t + 1,l}},{a_{t,l}};{W_{RL}}} \right)} } \right] \cdot R\left( {{u_l}} \right)} \right]\\ &\propto {\mathbb{E}_{{u_l} \sim p\left( {{u_l};{W_{RL}}} \right)}}\left[ {{\nabla _{{W_{RL}}}}\left[ {\bcancel{{\log p\left( {{s_{1,l}}} \right)}} + \sum\limits_{t = 1}^{{T_l}} {\log p\left( {{s_{t + 1,l}},{a_{t,l}};{W_{RL}}} \right)} } \right] \cdot R\left( {{u_l}} \right)} \right]\\ &\approx {\mathbb{E}_{{u_l} \sim p\left( {{u_l};{W_{RL}}} \right)}}\left[ {{\nabla _{{W_{RL}}}}\sum\limits_{t = 1}^{{T_l}} {\log p\left( {{s_{t + 1,l}},{a_{t,l}};{W_{RL}}} \right)} \cdot R\left( {{u_l}} \right)} \right]\\ &= {\mathbb{E}_{{u_l} \sim p\left( {{u_l};{W_{RL}}} \right)}}\left[ {\sum\limits_{t = 1}^{{T_l}} {{\nabla _{{W_{RL}}}}\log p\left( {{s_{t + 1,l}},{a_{t,l}};{W_{RL}}} \right)} \cdot R\left( {{u_l}} \right)} \right]\\ &=\sum\limits_{{u_l} \in \mathbb{U}} {p\left( {{u_l};{W_{RL}}} \right) \cdot \left[ {\sum\limits_{t = 1}^{{T_l}} {{\nabla _{{W_{RL}}}}\log p\left( {{s_{t + 1,l}},{a_{t,l}};{W_{RL}}} \right) \cdot R\left( {{u_l}} \right)} } \right]}\\ &=\sum\limits_l^{\mathcal L} {p\left( {{u_l};{W_{RL}}} \right) \cdot \left[ {\sum\limits_{t = 1}^{{T_l}} {{\nabla _{{W_{RL}}}}\log p\left( {{s_{t + 1,l}},{a_{t,l}};{W_{RL}}} \right) \cdot R\left( {{u_l}} \right)} } \right]}\\ &= \sum\limits_l^{\mathcal L} {\sum\limits_{t = 1}^{{T_l}} {p\left( {{u_l};{W_{RL}}} \right) \cdot {\nabla _{{W_{RL}}}}\log p\left( {{s_{t + 1,l}},{a_{t,l}};{W_{RL}}} \right)} \cdot R\left( {{u_l}} \right)}\\ &\approx \frac{1}{{\mathcal L}}\sum\limits_l^{\mathcal L} {\sum\limits_{t = 1}^{{T_l}} {{\nabla _{{W_{RL}}}}\log p\left( {{s_{t + 1,l}},{a_{t,l}};{W_{RL}}} \right)} \cdot R\left( {{u_l}} \right)}\\ &\approx \frac{1}{{\mathcal L}}\sum\limits_l^{\mathcal L} {\sum\limits_{t = 1}^{{T_l}} {{\nabla _{{W_{RL}}}}\log p\left( {a_{t,l}}, {{s_{t + 1,l}};{W_{RL}}} \right)} \cdot R\left( {{u_l}} \right)}\;\;(本文得出的推导结果)\\ &\approx \frac{1}{{\mathcal L}}\sum\limits_l^{\mathcal L} {\sum\limits_{t = 1}^{{T_l}} {{\nabla _{{W_{RL}}}}\log p\left( {a_{t,l}}, {{s_{t,l}};{W_{RL}}} \right)} \cdot R\left( {{u_l}} \right)}\;\;(论文得出的推导结果)\\ \end{aligned} \tag {15} ∇WRLJ(WRL)=Eul∼p(ul;WRL)[∇WRLlogp(ul;WRL)R(ul)]=Eul∼p(ul;WRL)[∇WRLlog[p(s1,l)Πt=1Tlp(st+1,l∣st,l,at,l)p(at,l∣st,l;WRL)]⋅R(ul)]=Eul∼p(ul;WRL)[∇WRLlog[p(s1,l)Πt=1Tlp(st+1,l,at,l;WRL)]⋅R(ul)]=Eul∼p(ul;WRL)[∇WRL[logp(s1,l)+t=1∑Tllogp(st+1,l,at,l;WRL)]⋅R(ul)]∝Eul∼p(ul;WRL)[∇WRL[logp(s1,l) +t=1∑Tllogp(st+1,l,at,l;WRL)]⋅R(ul)]≈Eul∼p(ul;WRL)[∇WRLt=1∑Tllogp(st+1,l,at,l;WRL)⋅R(ul)]=Eul∼p(ul;WRL)[t=1∑Tl∇WRLlogp(st+1,l,at,l;WRL)⋅R(ul)]=ul∈U∑p(ul;WRL)⋅[t=1∑Tl∇WRLlogp(st+1,l,at,l;WRL)⋅R(ul)]=l∑Lp(ul;WRL)⋅[t=1∑Tl∇WRLlogp(st+1,l,at,l;WRL)⋅R(ul)]=l∑Lt=1∑Tlp(ul;WRL)⋅∇WRLlogp(st+1,l,at,l;WRL)⋅R(ul)≈L1l∑Lt=1∑Tl∇WRLlogp(st+1,l,at,l;WRL)⋅R(ul)≈L1l∑Lt=1∑Tl∇WRLlogp(at,l,st+1,l;WRL)⋅R(ul)(本文得出的推导结果)≈L1l∑Lt=1∑Tl∇WRLlogp(at,l,st,l;WRL)⋅R(ul)(论文得出的推导结果)(15)
关于上述公式(15),有两点尚需要进行进一步确认:
- 公式(15)的倒数第二行和最后一行的log表达式中,本文推导得出的是 log p ( s t + 1 , l , a t , l ; W R L ) \log p\left( {{s_{t + 1,l}},{a_{t,l}};{W_{RL}}} \right) logp(st+1,l,at,l;WRL),与论文的表达式 log p ( s t , l , a t , l ; W R L ) \log p\left( {{s_{t ,l}},{a_{t,l}};{W_{RL}}} \right) logp(st,l,at,l;WRL)略有出入,需要进行进一步核实。
- 公式(15)的倒数第3行,可以发现,它同倒数第4行的关系是:将 ∑ l L ∑ t = 1 T l p ( u l ; W R L ) \sum\nolimits_l^{\mathcal L} {\sum\nolimits_{t = 1}^{{T_l}} {p\left( {{u_l};{W_{RL}}} \right)} } ∑lL∑t=1Tlp(ul;WRL)替换成了 1 L ∑ l L ∑ t = 1 T l \frac{1}{{\mathcal L}}\sum\nolimits_l^{\mathcal L} {\sum\nolimits_{t = 1}^{{T_l}} {} } L1∑lL∑t=1Tl并做了近似处理,相当于将加权求和变成了平均值。论文给出的解释是sample approximation(参考文献:Williams, R. J. (1992). Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine learning, 8(3-4), 229-256. 在线阅读),目前还需要弄清楚这里面的原理。
上式中的 R ( u l ) R\left( u_l \right) R(ul)是可以计算出来的,即 R ( u l ) = z T l , l R\left( u_l \right) = {z_{{T_l},l}} R(ul)=zTl,l,因此上式中的梯度是可以求解的。于是我们可以用随机梯度上升法来优化我们的目标函数,可得:
Δ W R L ∝ ∑ l = 1 L ∑ t = 1 T l ∇ W R L log p ( a t , l ∣ s t , l ; W R L ) ⋅ z T l , l (16) \Delta {W_{RL}} \propto \sum\limits_{l = 1}^\mathcal{L} {\sum\limits_{t = 1}^{{T_l}} {{\nabla _{{W_{RL}}}}\log p\left( {{a_{t,l}}\left| {{s_{t ,l}};{W_{RL}}} \right.} \right)} } \cdot {z_{{T_l},l}} \tag {16} ΔWRL∝l=1∑Lt=1∑Tl∇WRLlogp(at,l∣st,l;WRL)⋅zTl,l(16)
8.4 RL算法描述
在RL阶段,论文的算法可以划分为两个部分:training部分以及模拟跟踪部分(其中training需要调用模拟跟踪)。
算法中的数学符号含义可以参考论文笔记的第3节。
Algorithm 1 Training ADNet with reinforcement learning (RL)

在Algorithm 1中, F F F表示视频帧, G G G表示ground-truth, a a a表示动作, b b b表示跟踪结果的矩形框, d d d表示动作动态。在进行RL强化学习训练时,论文首先调用Tracker过程进行模拟跟踪,跟踪完成后,利用关键帧的ground-truth进行奖励评价,并根据奖励进行网络的反向传播training,更新网络权重。
Algorithm 2 Tracking Procedure of ADNet

在Algorithm 2中,其输入的参数有三个:
- 上一帧的定位bounding-box
- 截至上一帧的动作动态(相当于历史记录)
- 当前帧画面
算法接收了参数后,首先得到首次动作迭代的初始图像块 p t , l , ( t = 1 ) p_{t,l},\;(t=1) pt,l,(t=1),在动作迭代时,根据网络正向传播得到具有最高得分的动作,然后根据这个动作得到新的bounding-box和采样的图像块,如此往复不停迭代,直至达到停止条件(达到了停止动作,或者达到了最大迭代次数)。这样就能够确定目标在当前帧中的位置了。
9. Online Adaptation
在跟踪阶段,论文提出得算法进行了Online自适应,这里的自适应主要指对网络权重进行更新。
这里可以再回顾一下论文的网络结构:

在online adaption阶段,论文并非对所有的网络权重进行更新。论文固定 { w 1 , w 2 , w 3 } \left\{ w_1, w_2, w_3 \right\} {w1,w2,w3},更新 { w 4 , w 5 , w 6 , w 7 } \left\{ w_4, w_5, w_6, w_7 \right\} {w4,w5,w6,w7},原因在于: { w 1 , w 2 , w 3 } \left\{ w_1, w_2, w_3 \right\} {w1,w2,w3}是卷积层,它们对应通用的图像表示,而 { w 4 , w 5 , w 6 , w 7 } \left\{ w_4, w_5, w_6, w_7 \right\} {w4,w5,w6,w7}是全连接层,它们对应的是各个不同视频的信息(参考MDNet的网络结构设计:https://arxiv.org/pdf/1510.07945v2.pdf )
论文仅仅利用supervised learning对网络权重进行更新,在线更新权重的目的在于让跟踪器能够适应每一个视频中的不断变化的场景。论文on-line adaption的算法描述如下所示:
Algorithm 3 Online Adaptation of ADNet in Tracking

从算法描述可以看出,论文首先在视频第1帧里面进行采样及网络权重的更新。在视频后续的每一帧中,算法仍然调用Algorithm 2中的Tracker过程进行物体坐标的初步确定,然后判断该坐标的置信度,如果置信度过低,就进行重检测。另外,每隔若干帧,就更新一次网络权重,以适应视频中的场景变化。
10. 总结
本文提出了一种基于深度强化学习的视频目标跟踪方法,这种方法的新颖之处在于通过强化学习中的奖励机制使得深度网络能够自主决定该如何“靠近”目标物体。通过这种思想,论文避免了密集采样,也降低了训练数据的标注要求,适合用到专门的跟踪场景(缺乏通用的、开放的数据集,需要自己搭建训练数据集),为视频目标跟踪研究指出了一个新的思路。