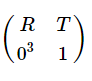视觉SLAM十四讲(一)基础知识
SLAM是Simultaneous Localization and Mapping的缩写,中文“同时定位于地图构建”。双目SLAM的距离估计是比较左右眼的图像获得的,非常消耗计算资源,需要使用GPU和FPGA设备加速。所以计算量是双目的主要问题之一。
基线:两个相机之间的距离,基线越大,能够测量到的物体越远。
回环检测:又称闭环检测,主要解决位置估计随时间漂移的问题,需要让机器人具有识别到过的场景的能力。
刚体运动:两个坐标系之间的运动由一个旋转加上一个平移组成。比如相机的运动,同一个向量在各个坐标系下的长度和夹角都不会发生变化,想象把手机抛到空中。
欧式变换:由旋转和平移组成。可以说刚体运动相差一个欧式变换。
欧拉角:它使用3个分离的转角,把一个旋转分解成3次绕不同的轴的旋转。欧拉角中常用的是使用“偏航-俯仰-滚转”3个角度来描述一个旋转。它等价于ZYX轴的旋转。欧拉角不适用于插值和迭代,往往只用于人机交互中。几乎不适用欧拉角表达姿态,同样也不会用在滤波或优化中使用欧拉角表示旋转(因为它具有奇异性)。欧拉角的一个重大缺点是万向锁问题,在俯仰角为正负90度的时候,第一次旋转和第三次旋转将使用同一个轴,使得系统失去一个自由度,这被称为奇异性问题。
四元数:它既是紧凑的,也没有奇异性,单位四元数表示三维空间中任意一个旋转。四元数使用之前需要归一化。
相似变换:比欧式变换多了一个自由度,它允许物体进行均匀缩放。
仿射变换:也叫做正交投影,与欧式变换不同,仿射变换只要求A是一个可逆矩阵,而不必是正交矩阵。
射影变换:最一般的变换,比如从真实世界到相机照片就是射影变换。
相机内参:在出厂之后是固定的,不会再使用过程中发生变化。需要自己确定相机的内参,叫做标定。
相机外参:相机的位姿R,T。外参会随着相机的运动发生改变。
相机畸变参数:畸变系数主要有下面几个:(k1; k2; p1; p2[; k3[; k4; k5; k6]] ,其中最常用的是前面四个,k1,k2为径向畸变系数,p1,p2为切向畸变系数。由透镜形状引起的畸变称为径向畸变。由于在相机的组装过程中不能使透镜和成像面严格平行称为切向畸变。将畸变后的点通过内参数矩阵投影到像素平面,得到该点在图像上的正确位置:
从像素坐标到世界坐标系:
即相机深度 Zc乘以像素坐标Px=相机内参K*相机外参RT*世界坐标Pw。
相机的运动:
(1)当相机为单目时,我们只知道2D的像素坐标,因而问题是根据两组2D点估计运动。该问题用对极几何解决。
(2)当相机为双目、RGB-D时,或者通过某种方法得到了距离信息,那么问题就是根据两组3D点估计运动。该问题通常用ICP解决。
(3)如果一组为2D,一组为3D,即,我们得到了一些3D点和它们在相机的投影位置,也能估计相机的运动。该问题通过PnP求解。
对极约束简洁的给出了两个匹配点的空间位置关系。于是,相机的位姿估计问题变为以下的两步:
(1)根据配对点的像素位置求出本质矩阵E或者基础矩阵F。
(2)根据E或者F求出R,T。
本质矩阵:
本质矩阵E有5个自由度,因此最少可以用5对点求解E。E在不同的尺度下是等价的。一般使用经典的八点法来求解E。八点法只利用了E的线性性质。E的内在本质是一种非线性性质。
从E分解得到相机的运动R,T。这个过程由奇异值分解(SVD)得到的。从E分解得到R,T,一共存在4个可能的解。幸运的是,只有一个解中点P在两个相机中都具有正的深度。因此,只要把任意一点代入4种解中,检测该点在两个相机下的深度,就可以确定哪一个解是正确的了。
单应矩阵:
单应矩阵通常描述处于共同平面上的一些点在两张图像之间的变换关系。它描述了两个平面之间的映射关系。若场景中的特征点都落在同一平面上则可以通过单应性进行运动估计。这种情况在无人机携带的俯视相机或者扫地机器人中携带的顶视相机中比较常见。自由度为8的单应矩阵可以通过4对匹配特征点算出(在非退化的情况下,即这些特征点不能有三点共线的情况)。
当特征点共面或者相机发生纯旋转时,基础矩阵的自由度下降,出现了所谓的退化。现实中的数据总包含一些噪声,这时如果继续使用八点法求解基础矩阵,基础矩阵多余出来的自由度将会主要有噪声决定。为了避免退化现象造成的影响,通常我们会同时估计基础矩阵F和单应矩阵H,选择重投影误差比较小的那个作为最终的运动估计矩阵。
三角测量:
通过不同的位置对同一路标点进行观察,从观察到的位置推断路标点的距离。三角测量是由平移得到的,纯旋转是无法使用三角测量的,因为在平移为零时,对极约束一直为零。平移较大时,在同样的相机分辨率下,三角化测量将更精确。
四元数:也可以用来表示旋转矩阵有不同的构造方式,如果使用Quaterniond q_wr=Quaterniond(0.55,0.3,0.2,0.2); 这种构造函数的话,实部在前,虚部在后,如果使用vector4d的构造方式,是实部放在后面虚部放在前面的,不同的构造方式在内存的存储都是虚部在前,实部在后的,所以取值的时候是虚部在前 实部在后的。四元数可作为复数的扩充,使用时必须归一化,单位化的四元数才表示一个旋转,因为类似复数一样,不归一化意味代表着缩放和旋转?如果不归一化意味着会发生尺寸变化,这与我们刚体运动的假设相悖?