【强化学习】Deep Q Network深度Q网络(DQN)
1 DQN简介
1.1 强化学习与神经网络
该强化学习方法是这么一种融合了神经网络和Q-Learning的方法,名字叫做Deep Q Network。
Q-Learning使用表格来存储每一个状态state,和在这个state每个行为action所拥有的Q值。而当今问题实在是太复杂,状态可以多到比天上的星星还多(比如下围棋)。如果全用表格来存储它们,恐怕我们的计算机有再大的内存都不够,而且每次在这么大的表格中搜索对应的状态也是一件很耗时的事。不过在机器学习中,有一种方法对这种事情很在行,那就是神经网络。我们可以将状态和动作当成神经网络的输入,然后经过神经网络的分析得到动作的Q值,这样我们就没有必要在表格中记录Q值,而是直接使用神经网络分析后得到动作的Q值,这样我们就没必要在表格中记录Q值,而是直接使用神经网络生成Q值。还有一种形式是这样,我们也只能输入状态值,输出所有的动作值,然后按照Q-Learning的原则,直接选择拥有最大值的动作当做下一步要做的动作。我们可以想象,神经网络接收外部的信息,相当于眼睛比子耳朵收集信息,然后经过大脑加工输出每种动作的值,最后通过强化学习的方式选择动作。
1.2 更新神经网络
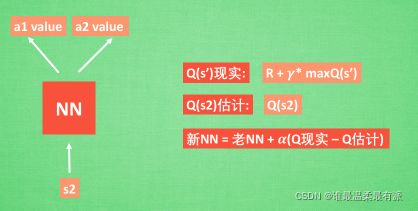
接下来我们基于第二种神经网络来分析,我们知道,神经网络是要被训练才能预测出准确的值。那在强化学习中,神经网络是如何被训练的呢?首先,我们需要a1,a2正确的Q值,这个Q值我们就用之前在Q-Learning中的Q现实来代替。同样我们还需要一个Q估计来实现神经网络的更新。所以神经网络的参数就是老的NN参数加学习率α乘以Q现实和Q估计的差距。我们整理一下
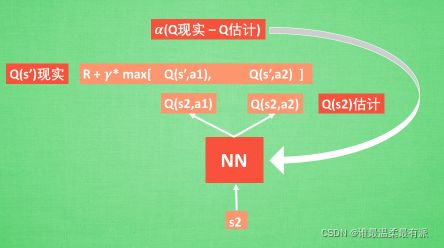
通过NN预测出Q(s2, a1)和Q(s2,a2)的值,这就是Q估计。然后我们选取Q估计中最大值的动作来换取环境中的奖励reward。而Q现实中也包含从神经网络分析出来的两个Q估计值,不过这个Q估计是针对于下一步在s’的估计。最后再通过刚刚所说的算法更新神经网络中的参数。但是这并不是DQN会玩电脑的根本原因。还有两大因素支撑着DQN使得它变得无比强大。这两大因素就是Experience replay和Fixed Q-targets。
1.3 DQN两大利器
简单来说,DQN有一个记忆库用于学习之前的经历。Q-Learning是一种off-policy离线学习法,它能学习当前经历着的,也能学习过去经历过的,甚至是学习别人的经历。所以每次DQN更新的时候,我们都可以随机抽取一些之前的经历进行学习。随机抽取这种做法打乱了经历之间的相关性,也使得神经网络更新更有效率。Fixed Q-targets也是一种打乱相关性的机理,如果使用fixed Q-targets也是一种打乱相关性的机理,如果使用fixed Q-targets,我们就会在DQN中使用到两个结构相同但参数不用的神经网络,预测Q估计的神经网络具备最新的参数,而预测Q现实的神经网络使用的参数则是很久以前的。有了这两种提升手段,DQN才能在一些游戏中超越人类。
2 DQN算法更新
2.1 要点
Deep Q Network 的简称叫DQN,是将Q-Learning的优势和Neual Networks结合了。如果我们使用tabular Q-Learning,对于每个state,action我们都需要存放在一张q_table的表中。如果像现实生活中,我们有千千万万个state,如果将这千万个state的值都放在表中,受限于我们计算机硬件,这样从表中获取数据,更新数据是没有效率的。这就是DQN产生的原因了。我们可以使用神经网络来估算这个state的值,这样就不需要一张表了。
2.2 算法

整个算法是在Q-Learning算法上加了一些修饰。Q-Learning算法可以点击这里回顾一下:https://blog.csdn.net/shoppingend/article/details/124291112?spm=1001.2014.3001.5501
这些装饰包括:记忆库(用于重复学习),神经网络计算Q值,暂时冻结q_target(切断相关性)
2.3 算法的代码行式
下面代码就是DQN于环境交互最重要的部分
def run_maze():
step = 0 # 用来控制什么时候学习
for episode in range(300):
# 初始化环境
observation = env.reset()
while True:
# 刷新环境
env.render()
# DQN 根据观测值选择行为
action = RL.choose_action(observation)
# 环境根据行为给出下一个 state, reward, 是否终止
observation_, reward, done = env.step(action)
# DQN 存储记忆
RL.store_transition(observation, action, reward, observation_)
# 控制学习起始时间和频率 (先累积一些记忆再开始学习)
if (step > 200) and (step % 5 == 0):
RL.learn()
# 将下一个 state_ 变为 下次循环的 state
observation = observation_
# 如果终止, 就跳出循环
if done:
break
step += 1 # 总步数
# end of game
print('game over')
env.destroy()
if __name__ == "__main__":
env = Maze()
RL = DeepQNetwork(env.n_actions, env.n_features,
learning_rate=0.01,
reward_decay=0.9,
e_greedy=0.9,
replace_target_iter=200, # 每 200 步替换一次 target_net 的参数
memory_size=2000, # 记忆上限
# output_graph=True # 是否输出 tensorboard 文件
)
env.after(100, run_maze)
env.mainloop()
RL.plot_cost() # 观看神经网络的误差曲线
3 DQN思维决策
代码主结构:
class DeepQNetwork:
# 上次的内容
def _build_net(self):
# 这次的内容:
# 初始值
def __init__(self):
# 存储记忆
def store_transition(self, s, a, r, s_):
# 选行为
def choose_action(self, observation):
# 学习
def learn(self):
# 看看学习效果 (可选)
def plot_cost(self):
初始值:
class DeepQNetwork:
def __init__(
self,
n_actions,
n_features,
learning_rate=0.01,
reward_decay=0.9,
e_greedy=0.9,
replace_target_iter=300,
memory_size=500,
batch_size=32,
e_greedy_increment=None,
output_graph=False,
):
self.n_actions = n_actions
self.n_features = n_features
self.lr = learning_rate
self.gamma = reward_decay
self.epsilon_max = e_greedy # epsilon 的最大值
self.replace_target_iter = replace_target_iter # 更换 target_net 的步数
self.memory_size = memory_size # 记忆上限
self.batch_size = batch_size # 每次更新时从 memory 里面取多少记忆出来
self.epsilon_increment = e_greedy_increment # epsilon 的增量
self.epsilon = 0 if e_greedy_increment is not None else self.epsilon_max # 是否开启探索模式, 并逐步减少探索次数
# 记录学习次数 (用于判断是否更换 target_net 参数)
self.learn_step_counter = 0
# 初始化全 0 记忆 [s, a, r, s_]
self.memory = np.zeros((self.memory_size, n_features*2+2)) # 和视频中不同, 因为 pandas 运算比较慢, 这里改为直接用 numpy
# 创建 [target_net, evaluate_net]
self._build_net()
# 替换 target net 的参数
t_params = tf.get_collection('target_net_params') # 提取 target_net 的参数
e_params = tf.get_collection('eval_net_params') # 提取 eval_net 的参数
self.replace_target_op = [tf.assign(t, e) for t, e in zip(t_params, e_params)] # 更新 target_net 参数
self.sess = tf.Session()
# 输出 tensorboard 文件
if output_graph:
# $ tensorboard --logdir=logs
tf.summary.FileWriter("logs/", self.sess.graph)
self.sess.run(tf.global_variables_initializer())
self.cost_his = [] # 记录所有 cost 变化, 用于最后 plot 出来观看
存储记忆,DQN的精髓部分止一:记录下所有经历过的步,这些步可以进行反复的学习,所以这是一种off-policy方法,你甚至可以自己玩,然后记录下自己玩的经历,让这个DQN学习你是如何通关的。
class DeepQNetwork:
def __init__(self):
...
def store_transition(self, s, a, r, s_):
if not hasattr(self, 'memory_counter'):
self.memory_counter = 0
# 记录一条 [s, a, r, s_] 记录
transition = np.hstack((s, [a, r], s_))
# 总 memory 大小是固定的, 如果超出总大小, 旧 memory 就被新 memory 替换
index = self.memory_counter % self.memory_size
self.memory[index, :] = transition # 替换过程
self.memory_counter += 1
选行为:
class DeepQNetwork:
def __init__(self):
...
def store_transition(self, s, a, r, s_):
...
def choose_action(self, observation):
# 统一 observation 的 shape (1, size_of_observation)
observation = observation[np.newaxis, :]
if np.random.uniform() < self.epsilon:
# 让 eval_net 神经网络生成所有 action 的值, 并选择值最大的 action
actions_value = self.sess.run(self.q_eval, feed_dict={self.s: observation})
action = np.argmax(actions_value)
else:
action = np.random.randint(0, self.n_actions) # 随机选择
return action
学习,这是最重要的一步,就是在Deep Q Network中,是如何学习,更新参数的。这里设计了target_net和eval_net的交互使用。
class DeepQNetwork:
def __init__(self):
...
def store_transition(self, s, a, r, s_):
...
def choose_action(self, observation):
...
def _replace_target_params(self):
...
def learn(self):
# 检查是否替换 target_net 参数
if self.learn_step_counter % self.replace_target_iter == 0:
self.sess.run(self.replace_target_op)
print('\ntarget_params_replaced\n')
# 从 memory 中随机抽取 batch_size 这么多记忆
if self.memory_counter > self.memory_size:
sample_index = np.random.choice(self.memory_size, size=self.batch_size)
else:
sample_index = np.random.choice(self.memory_counter, size=self.batch_size)
batch_memory = self.memory[sample_index, :]
# 获取 q_next (target_net 产生了 q) 和 q_eval(eval_net 产生的 q)
q_next, q_eval = self.sess.run(
[self.q_next, self.q_eval],
feed_dict={
self.s_: batch_memory[:, -self.n_features:],
self.s: batch_memory[:, :self.n_features]
})
# 下面这几步十分重要. q_next, q_eval 包含所有 action 的值,
# 而我们需要的只是已经选择好的 action 的值, 其他的并不需要.
# 所以我们将其他的 action 值全变成 0, 将用到的 action 误差值 反向传递回去, 作为更新凭据.
# 这是我们最终要达到的样子, 比如 q_target - q_eval = [1, 0, 0] - [-1, 0, 0] = [2, 0, 0]
# q_eval = [-1, 0, 0] 表示这一个记忆中有我选用过 action 0, 而 action 0 带来的 Q(s, a0) = -1, 所以其他的 Q(s, a1) = Q(s, a2) = 0.
# q_target = [1, 0, 0] 表示这个记忆中的 r+gamma*maxQ(s_) = 1, 而且不管在 s_ 上我们取了哪个 action,
# 我们都需要对应上 q_eval 中的 action 位置, 所以就将 1 放在了 action 0 的位置.
# 下面也是为了达到上面说的目的, 不过为了更方面让程序运算, 达到目的的过程有点不同.
# 是将 q_eval 全部赋值给 q_target, 这时 q_target-q_eval 全为 0,
# 不过 我们再根据 batch_memory 当中的 action 这个 column 来给 q_target 中的对应的 memory-action 位置来修改赋值.
# 使新的赋值为 reward + gamma * maxQ(s_), 这样 q_target-q_eval 就可以变成我们所需的样子.
# 具体在下面还有一个举例说明.
q_target = q_eval.copy()
batch_index = np.arange(self.batch_size, dtype=np.int32)
eval_act_index = batch_memory[:, self.n_features].astype(int)
reward = batch_memory[:, self.n_features + 1]
q_target[batch_index, eval_act_index] = reward + self.gamma * np.max(q_next, axis=1)
"""
假如在这个 batch 中, 我们有2个提取的记忆, 根据每个记忆可以生产3个 action 的值:
q_eval =
[[1, 2, 3],
[4, 5, 6]]
q_target = q_eval =
[[1, 2, 3],
[4, 5, 6]]
然后根据 memory 当中的具体 action 位置来修改 q_target 对应 action 上的值:
比如在:
记忆 0 的 q_target 计算值是 -1, 而且我用了 action 0;
记忆 1 的 q_target 计算值是 -2, 而且我用了 action 2:
q_target =
[[-1, 2, 3],
[4, 5, -2]]
所以 (q_target - q_eval) 就变成了:
[[(-1)-(1), 0, 0],
[0, 0, (-2)-(6)]]
最后我们将这个 (q_target - q_eval) 当成误差, 反向传递会神经网络.
所有为 0 的 action 值是当时没有选择的 action, 之前有选择的 action 才有不为0的值.
我们只反向传递之前选择的 action 的值,
"""
# 训练 eval_net
_, self.cost = self.sess.run([self._train_op, self.loss],
feed_dict={self.s: batch_memory[:, :self.n_features],
self.q_target: q_target})
self.cost_his.append(self.cost) # 记录 cost 误差
# 逐渐增加 epsilon, 降低行为的随机性
self.epsilon = self.epsilon + self.epsilon_increment if self.epsilon < self.epsilon_max else self.epsilon_max
self.learn_step_counter += 1
为了看学习效果,我们在最后输出学习过程中的cost变化曲线。
class DeepQNetwork:
def __init__(self):
...
def store_transition(self, s, a, r, s_):
...
def choose_action(self, observation):
...
def _replace_target_params(self):
...
def learn(self):
...
def plot_cost(self):
import matplotlib.pyplot as plt
plt.plot(np.arange(len(self.cost_his)), self.cost_his)
plt.ylabel('Cost')
plt.xlabel('training steps')
plt.show()
文章来源:莫凡强化学习https://blog.csdn.net/weixin_44466434/article/details/125481635