arduino 入门套件
Among the many disciplines in the field of machine learning, computer vision has arguably seen unprecedented growth. In its current form, it offers plethora of models to choose from, each with its own shine. It’s quite easy then, to lose your way in this abyss. Fret not, for this foe can be defeated, like many others, using the power of mathematics and a touch of intuition.
在机器学习领域的许多学科中，计算机视觉可以说是空前的增长。 在当前形式下，它提供了多种模型供您选择，每种模型都有自己的特色。 那么，很容易迷失在深渊中。 不要担心，因为可以像其他许多敌人一样，利用数学的力量和直觉来打败这个敌人。
Before we venture forth, it is important to have the basic knowledge of machine learning under your belt. To start with, we should understand the concept of convolution in general and then we can narrow it down to its application in machine learning. In hindsight, by convolution, we mean that a function strides over the domain of another function thereby leaving its imprint(Fig 1.).
在我们冒险之前，掌握机器学习的基础知识很重要。 首先，我们应该大致了解卷积的概念，然后将其缩小到机器学习中的应用。 在事后看来，通过卷积，我们的意思是一个功能跨越了另一个功能的域，从而留下了它的烙印(图1.)。
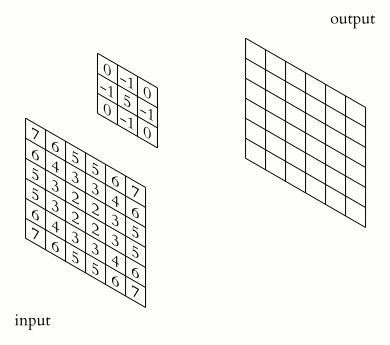
A computer can’t really “see” an image, all it can perceive are bits, 0/1. To comply with this lingo, we can represent images as a matrix of numbers, where each number corresponds to the pixel strength (0–255). We can then perform convolution by taking a filter window which strides over the image progressively(Fig 2.). Each filter is associated with a set of numbers which is multiplied to a portion of the image to extract a specific information. We employ multiple kernels to gather various aspects of the image. The end-goal is to learn suitable kernel weights which best encodes the data for our use case. This information capture process is what grants a computer the ability to “see”.
计算机无法真正“看到”图像，它只能感知到0/1位。 为了遵循这种术语，我们可以将图像表示为数字矩阵，其中每个数字对应于像素强度(0–255)。 然后，我们可以通过获取一个逐步跨越图像的滤镜窗口来进行卷积(图2)。 每个过滤器都与一组数字相关联，该数字与图像的一部分相乘以提取特定信息。 我们采用多个内核来收集图像的各个方面。 最终目标是学习合适的内核权重，从而对我们的用例进行最佳编码。 此信息捕获过程使计算机能够“查看”。
You might have noticed that down the neural net, the feature map tends to shrink. In fact, it is entirely possible for the image to vanish down the lane. In addition to that, the edges of the images get almost no say to the result since the filter passes through them only once. This is where the concept of ”Padding” debuts. Padding implies shielding our original image with an additional layer of zero value vectors. With this, we have already solved the first problem, i.e. feature map shrinking, with a smart choice of padding we can have the output feature map to have exact dimension as input, this is called “SAME PADDING”. This also ensures that the kernel filter overlaps more than once on the edges of our image. The case where we don’t employ this feature is called as “VALID PADDING”.
您可能已经注意到，在神经网络中，特征图趋于缩小。 实际上，图像完全有可能在车道上消失。 除此之外，由于过滤器仅通过图像一次，因此图像的边缘几乎没有发言权。 这是“填充”概念首次出现的地方。 填充意味着通过附加一层零值向量来屏蔽原始图像。 至此，我们已经解决了第一个问题，即特征图缩小，通过明智地选择填充，我们可以使输出特征图具有准确的尺寸作为输入，这被称为“ SAME PADDING” 。 这也可以确保内核滤镜在图像边缘上重叠不止一次。 我们不使用此功能的情况称为“有效填充”。
Any significant stride in technology must surpass its predecessor in every way. In this light, the thought arises, where exactly does the classic framework fall behind? This can be very easily explained once we examine the computational cost. Dense layer consists of a tight-knit connection between each and every layer and “each connection is associated with a weight”(Ardakani et al.). On the contrary, since convolution only considers a portion of the image, we can interpret it as a “sparsely connected neural networks”. In this architecture, “each neuron is only connected to a few neurons based on a pattern and a set of weights is shared among all neurons”(Ardakani et al.). The tight-knit nature of Dense Layers is the reason it has exponentially higher number of learnable parameters than Convolution Layers.
技术上的任何重大进步都必须以各种方式超越其前身。 有鉴于此，这种思想产生了，经典框架到底落在了什么地方？ 一旦我们检查了计算成本，这很容易解释。 致密层由每一层之间的紧密连接组成， “每个连接都与重量有关” (Ardakani等人)。 相反，由于卷积仅考虑图像的一部分，因此我们可以将其解释为“稀疏连接的神经网络”。 在这种架构中， “每个神经元仅基于一种模式连接到几个神经元，并且在所有神经元之间共享一组权重” (Ardakani等人)。 密集层的紧密本质是可卷积参数比卷积层指数增长的原因。
I think there are two main advantages of convolutional layers over just using fully connected layers. And the advantages are parameter sharing and sparsity of connections.
我认为卷积层比仅使用完全连接的层有两个主要优点。 优点是参数共享和连接稀疏。
-Andrew NG
-安德鲁(NG)
It is often observed that a convolutional layer appears in conjunction with a “Pooling” layer. Pooling layer, as the name suggests, down-samples the feature map of the previous layer. This is important as plain convolution latch tightly to the input feature map, this means even the finest distortion in the image may lead to entirely different results. By down-sampling, we get a summary statistic of the input thereby making the model translation invariant.
经常观察到，卷积层与“池”层一起出现。 顾名思义，池化层对上一层的特征图进行下采样。 这很重要，因为普通卷积紧紧地锁在输入特征图上，这意味着即使图像中最精细的失真也可能导致完全不同的结果。 通过下采样，我们可以获得输入的摘要统计信息，从而使模型转换不变。
Imagine an image of a cat comes in.
想象有一只猫的形象进来。
Imagine the same image comes in, but rotated.
想象一下有相同的图像进来，但是旋转了。
If you have the same response for the two, that’s invariance.
如果您对两者的响应相同，那就是不变性。
-source: Tapa Ghosh, www.quora.com
资料来源：Tapa Ghosh， www.quora.com
By “translation invariant” we mean it’s invariant to linear shift of the target image.
“平移不变”是指目标图像的线性位移不变。
Pooling layers cuts through these noises and lusters the dominant features to shine brighter. This provides immunity against these distortions and makes our model robust to changes. There are two of methods of sampling often employed
汇聚层消除了这些噪音，使主要特征更加明亮。 这样可以抵抗这些失真，并使我们的模型对更改具有鲁棒性。 经常采用两种采样方法
Average Pool: This takes a filter and averages over the image. This gives a fair-say to the nuances of the image. Often this method is not employed.
平均池：这将使用过滤器并对图像进行平均。 这可以公平地对待图像的细微差别。 通常不使用此方法。
Max Pool: Used prevalently, it takes the maximum of pixel values under its window. In this method, we take only the most dominant feature into consideration.
最大池：通常使用，它在其窗口下获取最大像素值。 在这种方法中，我们仅考虑最主要的特征。
It is important to note that, pooling layer in itself does not have learnable parameters. They are fixed size operations and they are set before training, a.k.a “hyper-parameters”. Some models e.g. MobileNet doesn’t rely on pooling layers for down-sampling instead “down sampling is handled with strided convolution”(Howard et al.).
重要的是要注意，池化层本身没有可学习的参数。 它们是固定大小的操作，它们在训练之前设置，也称为“超参数”。 某些模型(例如MobileNet)不依赖于池层进行下采样，而是“通过分步卷积处理下采样” (Howard等人)。
Convolutional neural network is now the go-to method for computer-vision problems. It’s introduction to this field has been a true game changer. It continues to be precise, faster and robust by the day but it’s roots nevertheless are humble.
卷积神经网络现在是解决计算机视觉问题的首选方法。 它对这一领域的介绍确实改变了游戏规则。 它一直保持着精确，快速和强大的优势，但其根基却是谦虚的。
参考书目 (Bibliography)
Ardakani, Arash, Carlo Condo, and Warren J. Gross. “Sparsely-connected neural networks: towards efficient vlsi implementation of deep neural networks.” arXiv preprint arXiv:1611.01427 (2016).
Ardakani，Arash，Carlo Condo和Warren J. Gross。 “稀疏连接的神经网络：迈向深度神经网络的高效vlsi实现。” arXiv预印本arXiv：1611.01427 (2016)。
Andrew Y. Ng, “Why Convolutions?”, www.coursera.org
吴安德(Andrew Y. Ng)，“为什么卷积？”， www.coursera。 组织
Howard, Andrew G., et al. “Mobilenets: Efficient convolutional neural networks for mobile vision applications.” arXiv preprint arXiv:1704.04861 (2017).
霍华德(Andrew G.)等。 “ Mobilenets：针对移动视觉应用的高效卷积神经网络。” arXiv预印本arXiv：1704.04861 (2017)。
翻译自: https://medium.com/analytics-vidhya/starters-pack-for-computer-vision-779b240cb045
arduino 入门套件